studiot

I agree but this is a duplicate thread of this one

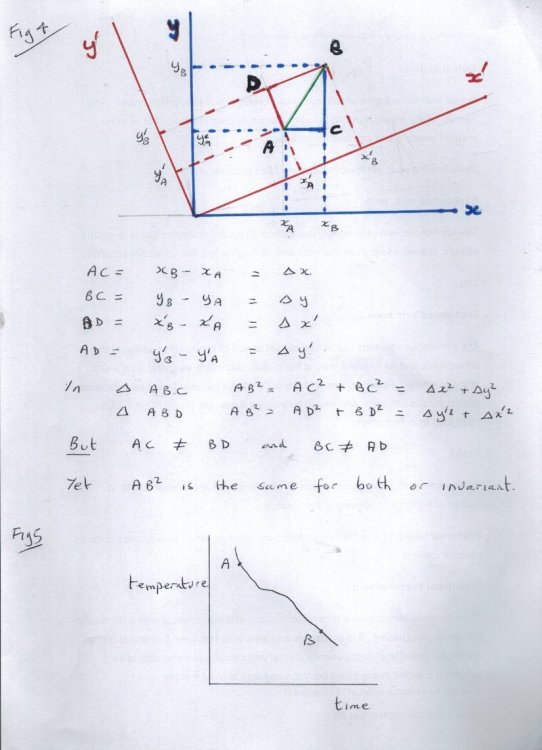
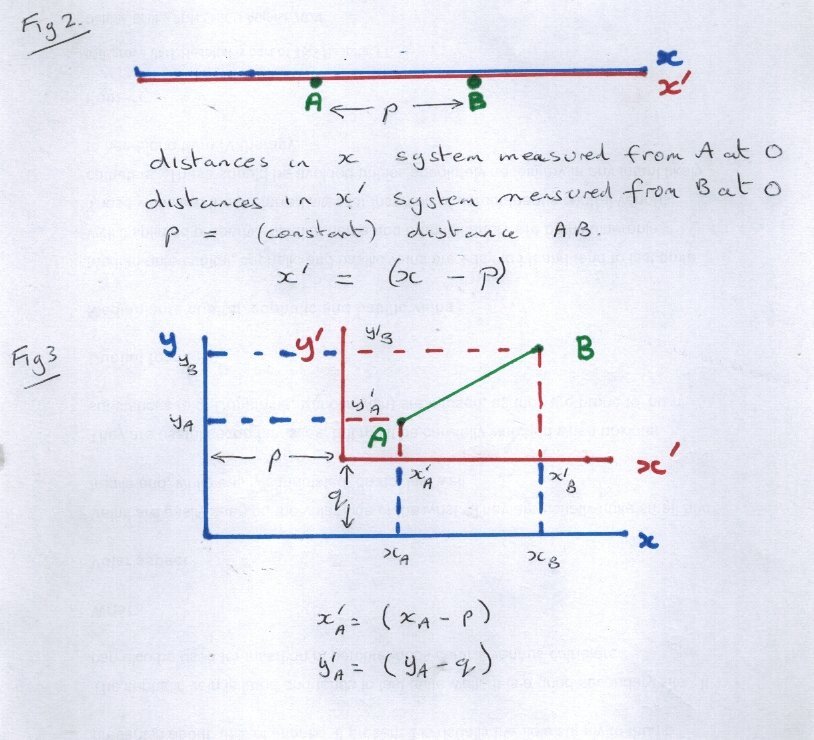
Ok so I have been doodling over the weekend, but sadly did not get as far as I had hoped. So here is the next part. Fig 2 is a repeat of Fig 1 but introducing two coordinate systems. In the red corner we have the red system. x', and in the blue corner we have the blue system x. Note the constant p yields a 'transfomation' equation between the two systems. We can also show that the the distance between A and B have the same value in both systems, following the equations in Fig1. That is it is invariant. I will return to the x' = (x - p) equation in more detail, when we get on to motion. In Fig 3 we strike out in 2 dimensions, with two displacement constants, p and q. Now that we are using the full extent of our graph paper, I have tilred the line AB, shown in green. Hopefully it is easy to see that the length of this line is [math]\sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} = \sqrt {{{\left( {x{'_B} - x{'_A}} \right)}^2} + {{\left( {y{'_B} - y{'_A}} \right)}^2}} [/math] although the coordiante differences are different for the red and blue systems. Displacement of a coordinate system is a 'permitted transformation' that simply move the origin about on the graph paper. The other permitted transformation is a rotation of the soordinate system, as in Fig 4 I have gone explicitly through the geometry to show how once again the length AB or its square AB2 is invariant, regardless of the angle of rotation. The key to this is to note that the length AB is the common hypotenuse to two triangles, ABC in the blue system and ABD in the red system. So for rotation also the length is measured the same in both systems That wraps up the static situation, but what ae we actually doing ? We are drawing lines on a piece of graph paper. All lines on that graph paper have a length measured in, say, cm. That is both axis lines, gridlines and plotted lines. To attach meaning to this look at Fig 5, which is a cooling curve for some substance, and a 'plot' of temperature against time. What units is the distance along the curve between points A and B measured in ? Well like all lines on the graph paper, it is measured in cm But, you say, the axes are in seconds and degrees C. No they are also measured, on the graph, in cm. Bot axes are subject to a scale factor (constant in this case) that introduces the necessary conversion of units. Cm to seconds and cm to degrees, remembering that we can only plot cm on the graph paper. This is where you question about c comes in. c is a velocity and velocity is a (variable or constant) scale factor converting time to length. The next installment will introduce moving coordinate systems, which are the basis of relativity. There are three things we must take forward from this. Firstly that there are invariants that are measured the same in all coordinate systems. Secondly The most important one is a function of coordinate difference, not the coordinates themselves. Thirdly that all we have been considering is Geometry, as in the shape and size of things.

And yet they are popular in Scandinavia. I have no idea what you mean by this ?

Some explanation of your diagrams would help and perhaps draw more discussion. I, for one, have no idea what you are showing in your diagrams. Perhaps also you could fill in the blank space following your here is some more comment ?

I suggest another way of looking at it is to say that classical mechanics (of the sort we have been talking about) is about localisation, quantum mechanics is about delocalisation. I was at Loughborough in 1968, 69 and 70. The Chemistry department was dwarfed by the Chemical Engineering department. The Physics department was even smaller than the Chemistry. But that is all a long story.

Seems to me that the 'environment' is shown at the sides (ends) of the waveforms using the standard ground symbols. The particle in a box is certainly not isolated since it is in a box. QM does offer an analysis of a body under no constraints ie a freely moving particle. But then a free body diagram with no replacement forces is a bit trivial.

I can't resist this, although google fought man and boy to resist offering anything for hat pump. As to your legitimate question. Yes some extra loft insulation was done but things like cavity wall, high grade double glazing, swapping old metal frames for solid mahogany, underfloor insulation were all done years before the heat pump. No costs of the extra loft insulation were included in the opening post.

I have a great deal of respect for Proff Atkins and several of his books. Funny, when I was first at university most of the important names of british chemistry books were light blue, eg Moelwyn-Hughes. One thing that I recall is the difference between classical and quantum systems. You cannot divorce a quantum system from its environment, there are no 'free body diagrams' in QM.

To answer in your own words and stop hijacking mine with off topic material ?

Thanks for pointing out my spelling error.

I suppose it depends how you weigh out your crimes. The theft of a loaf of bread or a clean new pair of trousers, when you don't have enough money for food, shelter etc, = 2 crimes or 2 criminals. Whereas mass murder by the million, when you have more than enough of everything, counts as only one ?

What experience and figures do you present to back up this claim ?

I get the impression from the News that the biggest crimes are committed by some of the most influential/richest/important people. So it is neither true nor fair to conflate being poor and being a criminal.

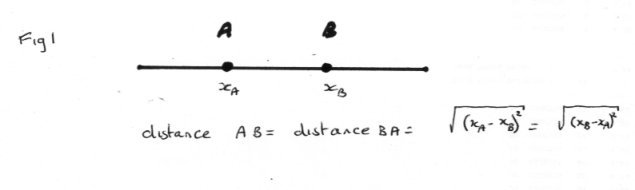
Ok to continue where I left off. Just to point out that I am offering backgound explanations and insights that you won't find in any one textbook. If you just want a formal development, there are many good presentations on offer. The official title is not 'spacetime' but 'the spacetime continuum'. A continuum is a grid or framework of points where at every point the properties of interest are the same. This expresses the idea of homogeneity, which is also inherent in the Principle of Relativity. For instance take a piece of squared graph paper. It is a continuum. A geometric continuum. A finite continuum, since the paper has edges, but a continuum nonetheless. The graph paper has no 'origin'. We can impose an origin at any point by imposing a pair of axes. And impose scales marked on the paper. This then gives a particular coordinate system to the grid. It also gives us a large number of possible different coordinate systems. I will start with static coordinate systems (which do not need time) before proceeding to moving coordinate systems (which do need time). For completeness I will start with one dimensional (ie one axis only, the x axis) coordinate systems. Coordinate systems are also called 'frames' , and will introduce the motivation for this name. The importance of one dimension is that it gives us a definition of length or distance between any two points A , B in the continuum as in fig (1). We use the rather awkward looking square root of the square of the difference in coordinates, xA and xB because this makes the distance from A to B the same as the distance from B to A and also makes this a positive or zero (ie nonnegative) quantity, which is only zero if A and B are the same point. [math]\sqrt {{{\left( {{x_A} - {x_B}} \right)}^2}} = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2}} [/math] Note. This conforms to the mathematics definition of a metric or distance function. Metrics in Physics can also be negative and Relativity explores what happens when the metric in Physics is negative. Another mathematical nicety is that the modulus or absolute value |xA-xB| can also be used as a metric, but has the disadvantage that it is not differentiable at zero. Work in progress to be continued.

The two electrons in a ground state hydrogen molecule are entangled (by spin). The two electrons in two separate hydrogen atoms are not. The process of bonding is also a process of entanglement. But entanglement is really off topic for a discussion of linewidths related to quanta. However this brings me back neatly to the question bangstrom keeps avoiding. If an electron in a ground state hydrogen molecule absorbs em radiation, thereby being promoted to an excited state. Which happens first ? The absorbtion or the promotion ? Or is bangstom promoting the idea that a system can exist in two different states simultaneously ?

Yes, is is the famous square root of minus 1 [math]i = \sqrt { - 1} [/math] The purpose of i is twofold. To rotate the axis in an imaginary direction. To turn a + into a minus, so not i does not appear on both sides of the equation since [math]{(ict)^2} = {i^2}{c^2}{t^2} = - 1{c^2}{t^2} = - {c^2}{t^2}[/math] Yes I am going to take time out of explaining graphs and frameworks and also because sometimes a peek ahead is motivational and I propose to use the just the x and t axes for this peek. I was going to say that If you are an electrical engineer, that I hope you know enough mechanics to work from Newton's laws to the Principle of Relativity. However you have answered that so I will introduce the diagrams. Nowhere is this more true than in Relativity. It is worth knowing that there are lots of different ways to arrive at SR and GR, but they all start with two basic Principles for SR and a third is added for GR. Different authors express these Principles in different ways, most suitable to their route. The strategy I am following is to look for relationships where one measurement is identical to another. Such situations lead to invariants. One such is called the form invariant, which is employed in the Principle of Relativity The idea is that a physical law must not depend upon the coordinate system. That is it should have the same form in all relevant coordinate systems. As an example take two particles A and B, interacting though some force F(xA, xB) and consider their equations of motion in one dimension (the x axis) Newtons tells us that if mA and mB are their respective masses and xA, xB their x coordinates then [math]{m_A}\frac{{{d^2}x}}{{d{t^2}}} = F\left( {{x_A},{x_B}} \right)[/math] and [math]{m_B}\frac{{{d^2}x}}{{d{t^2}}} = - F\left( {{x_A},{x_B}} \right)[/math] Now suppose we describe these same two particles in acoordinate system whose origin is at x0 in the original system and call this new system the x' system. Then xA = x'A + x0 and xB = xB + x0 Substitute these two equations into the first two we get [math]{m_A}\frac{{{d^2}x'}}{{d{t^2}}} = F\left( {x{'_A} + {x_0},x{'_B} + {x_0}} \right)[/math] and [math]{m_B}\frac{{{d^2}x'}}{{d{t^2}}} = - F\left( {x{'_A} + {x_0},x{'_B} + {x_0}} \right)[/math] since x0 is a constant [math]\frac{{d{x_0}}}{{dt}} = 0[/math] So the forces of interaction do not have the same form (are not form invariant) as in the original coordiante system. If they did they would be [math]{m_A}\frac{{{d^2}x'}}{{d{t^2}}} = F\left( {x{'_A},x{'_B}} \right)[/math] and [math]{m_B}\frac{{{d^2}x'}}{{d{t^2}}} = - F\left( {x{'_A},x{'_B}} \right)[/math] And the new equations depend upon the origin x0 of the new system. So Newton's equatiosn, as they stand do not conform to the Principle of Relativity. However all is not lost. the remedy is to work with coordinate differences, not directly with the coordinates so we write F(xA,xB) = f(xA - xB) yielding equations of motion in the new system in the required form [math]{m_A}\frac{{{d^2}x'}}{{d{t^2}}} = f\left( {x{'_A},x{'_B}} \right)[/math] [math]{m_B}\frac{{{d^2}x'}}{{d{t^2}}} = - f\left( {x{'_A},x{'_B}} \right)[/math] This is the motivation for using the pythagorian square root of the sum of the squares of the coordinate distances I mentioned in an earlier post.

Yeay excellent progress! A retired Engineer is good, some calculus is better, but not not essential now we have agreed that speed is given by dx/dt. If you would like to indicate what sort of Engineer, (electrical, mechanical etc) I will try to pick my examples from that. The important point is that the axes (x,y,z,t or x,y,z,ct) form a euclidian framework to work with. Einstein originally worked with the first set but his friend and maths advisor, Minkowski, realised that the second set offered theoretical and calculational simplicity, but sadly died not long afterwards. Minkowski took the standard euclidian distance between two points A (x1 , y1, z1) and B (x2, y2, z2, ) which is given by [math]\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} [/math] and extended it to include time. So he faced the same question you are asking which is the time intervals are not lengths. Einstein had already implicitly covered this in his rendering of his Special Relativity equations, including the multiplication by c, but Mikkowski's is more elegant. Minkowski offered that if we not only convert the fourth axis of the framework to a length but get it to point somewhere other than along an already used space axis, we can extend the above formula for the 'distance' between two points, making the time axis a length but a bit different from the others. He did this by multiplying by ic so the expression becomes [math]\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2} + {{\left( {ic{t_2} - ic{t_1}} \right)}^2}} [/math] or [math]\sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2} + \Delta {{\left( {ict} \right)}^2}} = \sqrt {\Delta {x^2} + \Delta {y^2} + \Delta {z^2} - \Delta {{\left( {ct} \right)}^2}} [/math] This was a masterstroke. I will explain further and draw some diagrams once you have confirmed you are OK with this maths.

I would just like to point out that there is only one 'wavefront' - a better term than wave edge. This demarcates the boundary between the zone of space occupied by the wave and the zone where the wave has not yet reached.

+1 However here is a rendering of what us Brits do expect of far flung cousins.

Thank you for your reply. A pity you only bothered to comment on a small part of my last post so I don't know what you made of the rest of it. As regards the reply, "too short to observe by any means" is not quite the same as my proposal for the Earth as a point particle. It is necessary so show that the process is too short to observe, just as we have to show (and do) that the actual size of the Earth makes an insignificant difference to our calculations. Now entanglement is a process, which begins with two or more particles that are not entangled. At this time they cannot act as though they were entangled. At some time later they can definitely act as entangled particles. You need to show that the time difference between these two situations, states whatever you care to call it, is insignificant to whatever calculations you are making. Then you can say the magic words "May be regarded as Instantaneous. for my purposes." Just as with the Earth, it does not mean that the Earth actually has zero size or that the time interval is actually instantaneous. This definition is common in Engineering, for example with "Instantaneous water heaters".

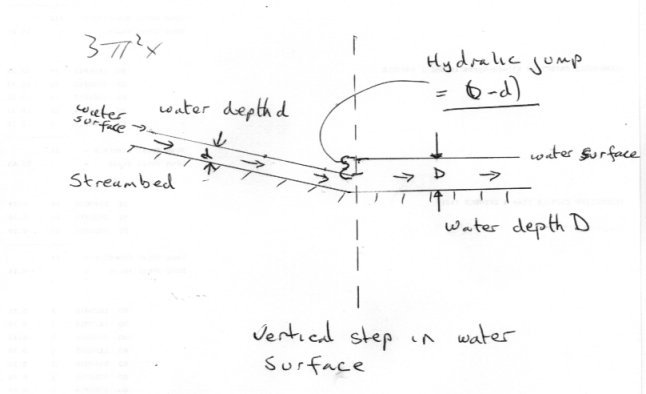
It is really worth considering what is inherent in the best model we have and the phenomenon itself. Are there any truly instantaneous natural processes ? Or is it just that our best model offers this ? Or is is like the concept of a point particle where we can say the size of the particle is insgnificant compared to the size of the system under consideration. So does instantaneous really mean: of insignificant duration compared with the timescale of the process under consideration ? Here is a classical example to think about for comparison. In open channel hydraulic flow there is a phenomenon where the level of the water surface changes (rises) abruptly. This is called a hydraulic jump. The jump occurs where there is a sudden levelling off of the bed slope so the water coming down the slope is moving faster than the water in the level part. The very best hydraulic models (equations) that we have predict this is an instaneous rise, over zero distance, but in reality the 'vertical' part of the water surface always slopes slightly forward. So there is a process which forms of a step in the water surface with a definite start and end point in time and space over very short intervals. The step is due to the fact that the incoming faster water has more kinetic energy than the outgoing slower water. So the surface must rise to transfer the energy to pressure energy.

However you chose to classify it, the fact that we need a 'natural linewidth' , is an indication that the process is not instantaneous. And whether or not is is instantaneous is the subject of my comment. Since it is not instantaneous, it makes sense to discuss the duration of the transition, just as it makes s ense to take other effewcts and mechanisms into account.

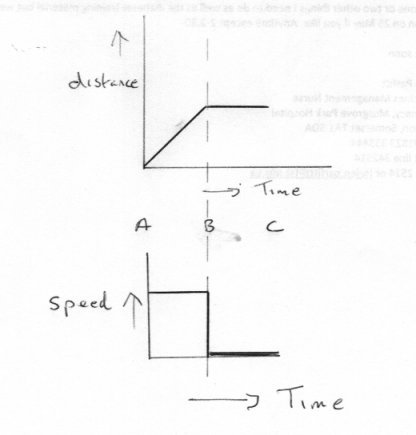
Once again you are right to question that which you do not understand, Eise has caught my drift. However I am more concerned with this problem that needs to be resolved first of all. This is very important because you have a basic misunderstanding here. Here is a sketch of a distance-time graph linked to a speed-time graph. They have common sections A_B and B_C In the section A_B the body is proceeding at constant speed (note I say speed not velocity since we are only plotting the magnitude, not the direction), So the distance is increasing linearly form A to B. At B the body stops still so time continues but the distance remains constant from B to C. The lower curve shows the speed from A to B as some (positive) value. Whilst the speed from B to C is also constant at zero. If you measure the slope of the distance - time line you will find it gives you the numerical value of the constant speed. As you can see we are trying to help you. In turn it would help us to have an idea where you are coming from. That is what is your approximate level of knowledge, for instance do you know any calculus ?

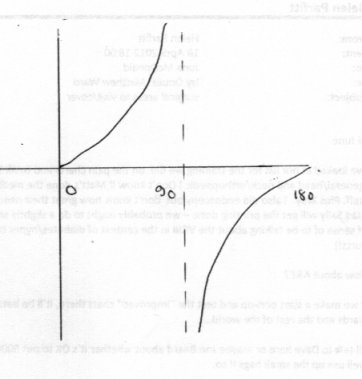
Just to add an illustration for Markus (and return the favour) Here is a sketch illustration of the tangent function and its singularity at 90o. The ctangent function is said to 'pass through infinity' at and angle of 90o, where it incurs a change of sign. This illustrates Markus statement that Since there is nowhere on the manifold (which is the plane of the paper) where the tan of 90 exists. It also illustrates his point that there are different types of singularity just as I previously said there are differnt types of infinity.

I said absolutely nothing about electrons or orbits or quantum leaps through soace or time or wormholes or any such stuff. But I did ask a fundamental question about the sequence of events. Re phrasing for absorbtion, Are you telling me you that the electron can 'jump' before absorbtion takes place ? Surely the fundamental question is Which must happen first, absorption, or the electron transition ? or as swansont puts it The 'lifetime' is a convenient model to work (mathematically) with this concept, as is the resultant 'natural linewidth'. You should also note in the hyperphysics link they point out that the broadening due to lifetime is orders of magnitude less than other broadening mechanisms