studiot

Oh ??

These are not palindromes but still useless but interesting 122 = 144 reverse the digits 212 = 441 and 132 = 169 reverse the digits 312 = 961

They are opposite in th UK and some European countries. Germany has a particularly stupid and in my opinion dangerous rule where an intersection is traffic light controlled. The Netherlands (Holland) has good implementation for (almost) all road users from pedestrian to non motorised vehicles to motorised vehicles (but not equestrian) Equestrians have priority in the UK.

Did you never watch Star Trek ? https://www.google.co.uk/search?source=hp&ei=b41YX66dE9GdjLsPnMObsA4&q=this+is+life+jim+but+not+as+we+know+it&oq=this+is+life+Jim+but+&gs_lcp=CgZwc3ktYWIQARgAMgIIADIGCAAQFhAeMgYIABAWEB46DgguELEDEMcBEKMCEJMCOggIABCxAxCDAToLCC4QsQMQxwEQowI6BQgAELEDOggILhDHARCjAjoICC4QsQMQgwE6CwguELEDEMcBEK8BOggILhCxAxCTAjoFCC4QsQM6AgguOggILhDHARCvAToLCC4QxwEQrwEQkwI6BQguEJMCUIYKWM5KYK5eaABwAHgBgAHeBYgB4CSSAQ0yLjcuMi4xLjIuMi4xmAEAoAEBqgEHZ3dzLXdpeg&sclient=psy-ab The great thing about English is that its evolution was brought about by user development, not by dictat from an official language institution. In time I don't doubt that many of today's inconsistencies will die out. The relationship between pronunciation and spelling is also varied. For instance Sulphur v sulfur are both pronounced the same way Aluminium v aluminum are not

I am wondering about the wisdom of looking at more powerful oxidising agents to counter the supposed mild oxidisation. I think in fact that yellowing and increasing opacity is a feature of life, particularly with artificial plastics materials. Change of mechanical properties eg embrittlement is another. The Materials Science behind this is complex and produced by several different factor. Some of these are irreversible.

A simple international agreement on standardising who has right of way at intersections would also help.

I wonder what English speakers around the world think of this ? https://www.bbc.co.uk/news/education-53941008 The article compares existing spelling with proposed new versions, using passages from Shakespeare's Hamlet. So troubles becomes trubles. The are examples of some writing characters that are even worse than my hand script as well.

" the book specifically tells you what omega is in problem 2! There the equation is d^2x/dt^2= omega x." Seems to me that example 2 starts with [math]\frac{{{d^2}x}}{{d{t^2}}} = - {\omega ^2}x[/math] Did you know that you can expand the attachment so that you don't need a magnifying glass to read it.

Thank you for that most interesting link. +1 I had not come across the material and Wiki is to be congratulated on bringing a lot of stuff together.

Yeah, thousands, hundreds tens, units fractions, and so on. I don't see it as off topic though.

If the digits were truly chosen at random, with a sample size of 22 I would expect pretty well all the numbers between 0 and 9 to appear twice. Spikey is a good word for it because there would be some 3s and some ones, But it would not cluster round a centre number like this data set. As a matter of comparison. When folks are asked to choose a number between 1 and 10, by far the most popular choice is 7. (Wikipedia) So a bell curve would indicate something like that going on. Another indicator is the frequency of entries in each decade ( I haven't checked this) A sample size of 22 is getting towards usual control sample sizes (30 is the British Standard for concrete cubes and other 'cusum' quality control charts ) for the normal distribution. But I'm beginning to sound like the weather man on TV with loads of useless facts and figures.

Sure. There are 22 different numbers on the sheet (ignore the arrows). So there is only one that begins with a zero - 0.668 near the top right. Further down on the right there are three numbers that begin with a 4, one above the other. 447 ; 423298 ; 487643 and so on for the rest. Moths table has two columns. The left hand table lists the digits 0 through 9, though why he has put 0 at the end I don't know. The right hand column shows the number of occurences of these digits in the 22 numbers on the sheet. It is called a frequency table and the numbers in the right hand column are the frequencies of occurence of each specific digit.

Interesting thanks. +1 How does a 'bell type curve' of 22 digits around an average of 5.36 indicate a random choice of first digit?

Sorry I hadn't noticed this before. Let us pretend you haven't contradicted yourself, and analyse the overall sytem and subsystems. The system is isolated The subsystems are open. All have internal energy. The particles have kinetic energy, which does not change unless they hit something. The instant a particle crosses (say from D to A as in the example), and before it hits anything in A its KE cannot change. So sub system A gains this KE and subsystem D looses it. Since there is no change of KE, no work is done and the First law tells us that the change must therefore be purely due to a heat transfer. (Which is to be epected) Whilst that must lead to a change in entropy of both A and D, how does that lead to a change of entropy of the overall system?

+1 for trying to bring yourself up to speed on waves and or asking questions where you are not sure of something. The Khan Academy has a good reputation. It also fits well with what I was trying to say. Notably that it is a good idea to at least look at, if not study deeply, classical waves before trying for Quantum waves, which are more difficult. This is not least because many of the classical ideas are directly transferable, although there are some stark differences. Although the combination of quantum waves is one of the most common processes on Earth, if not in the Universe, it is purely abstract in that we can't directly grab hold of it like we can with classical waves in a wave tank or on a string . Another word for combination of quantum waves is chemical reactions. That is the main situation where you have the quantum waves of two electrons involved. To answer your questions about travelling waves, which are good ones that show you have read carefully what I wrote, yes it is important to understand why. These are one of several 'wrinkles' to get clear as they are amongst the things that transfer (in some way) from classical to quantum, but the ideas are easier to introduce in a classical setting. Luckily they are easy to elucidate, but I will need to draw some more diagrams. Do you understand what a sine a cosine and a tangent are in trigonometry or anything else ? (The blue curve I originally posted is part of a sine wave),

Hopefully you have read the rules here, in which case you will know you have only 2 more posts available in the next 22 hours. So I suggest you think very carefully before making any more and come up with some proper explanation of what this is all about. You have already been asked for that by two other members.

How many forums are being spammed ? https://mathforums.com/threads/black-hole-maths-puzzle.350271/

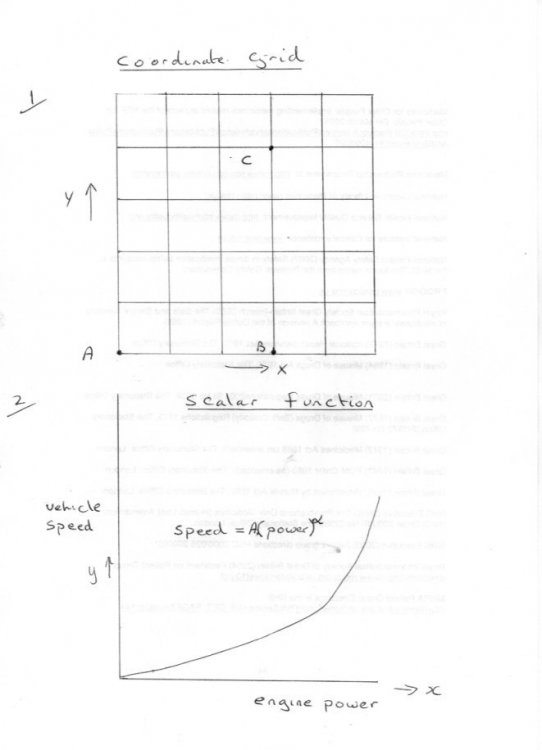
Swansont and Joe have both said more or less the same thing and given some examples. In particular there is a heirarchy or ladder; I have pointed out that vectors are not the top of the ladder. ...... Vectors Scalars Numbers So what are the differences and how do you tell these differences? It is a little more tricky than at first sight, as Joe has hinted since distance can be a scalar or a vector, depending upon circumstances. But let us start at the bottom. Numbers and scalars. Not all numbers are scalars. 3 and 5 by themselves are just numbers. You can add them together 3 + 5 = 8 Give them units eg 3 apples, 5 oranges. You cannot add these together 3 apples plus 5 oranges is always 3 apples plus 5 oranges (unless we rename them both fruit). You can, however add 3 apples and 5 apples to get 8 apples. So sometimes you can add scalars - but only if they ahae the same units and they apply to the same situation. 4 kg plus 4 kg is only 8 kg if they are on the same side of the scales. You can always add two any numbers to obtain a sum number without restriction Note swansont said scalars usually have units. Sometimes a scalar can be just a number. This is, in fact, where the name comes from, An enlargement of 1.2 or 120% on you photocopier is just a number, as is the scale factor on a map But adding the scale of one map to the scale of another makes no sense. And if you enlarge by 1.2 twice you do not get an enlargement of (1.2 + 1.2 =2.4) you get an enlargement of (1.2 * 1.2 = 1.44) So a number can be a scalar (one step up the ladder) or it can be just a number. Similarly Joe has noted that distance can be a scalar, with units, or it can be one step up the ladder as a vector. Talking of maps neatly brings us to coordinate systems where we can start to look at the differences between scalars and vectors. I assume you are familiar with plotting a graph of a function ? That is a form of coordinate system. We do not need fancy coordinates systems, a simple X - Y grid as in Fig 1will suffice. The important points are that X and Y are variables that on take on any value - that is we can choose any value for Y without regard to the value of X. So we can place A, B and C where we like on the grid. We say that X and Y are both independent variables and we need (at least) two of them to create a vector. Before we come to that, The graph plotted in fig 2 relates to swansont's example of speed and velocity. Both speed and power are scalars. The speed of our vehicle depends upon the power supplied by the engine. So we cannot place A, B and C anywhere on the XY plot we are constrained by the relationship between X and Y In this case we say that We say that X is an independent variable and Y is a dependent variables We will examine the significance of this when we come to plot vectors in the next instalment, along with the significance of the units of scalers for the addition of vectors. How are we doing?

Thank you for sharing that, I found it very interesting. People have a desire to keep numbers and quantities they are working with to within small number limits. Very often when the numbers start to get large or spread out they introduce a new unit 1 foot, 2 feet, 3 feet or 1 yard. This is not infallibles since other requirements pull in other directions eg the need for finer measurement 12 innches or 1 foot.

Why do you find this surprising ? I don't find it at all surprising, how often does your shopping include 1 pineapple or cabbage and how often 9 pineapples or cabbages?

Ther's more than one possible reason for this so see a specialist eg https://www.mayoclinic.org/diseases-conditions/sweating-and-body-odor/symptoms-causes/syc-20353895

How for the entire isolated system? Again how for the entire system ?

The title says nothing about QM, and as I already noted, there are legitimate and worthwhile implementations/uses of the single, double and multiple slit experiments. It is clear that the OP would like to learn and get straightened out some misconceptions, not least that he has mixed up classical wave theory and QM, which is very common. It is also clear to me that a poor presentation of much more difficult material has been partly responsible for this, along with a shaky foundation of the whole subject. I was simply trying to shore up this foundation at an acceptable level, so I am sorry you clearly think I have failed, particularly in my attempt to build up the background material. So I will leave you to to explain the finer details of QM to a beginner who is clearly aware that he hasn't yet appreciated what constitutes a wave, let alone a wave function which is something else again. I apologise for my intrusion in this thread.

Thank you for your confidence. I must go tonight, but I will draw some (hopefully helpful) diagrams tomorrow.

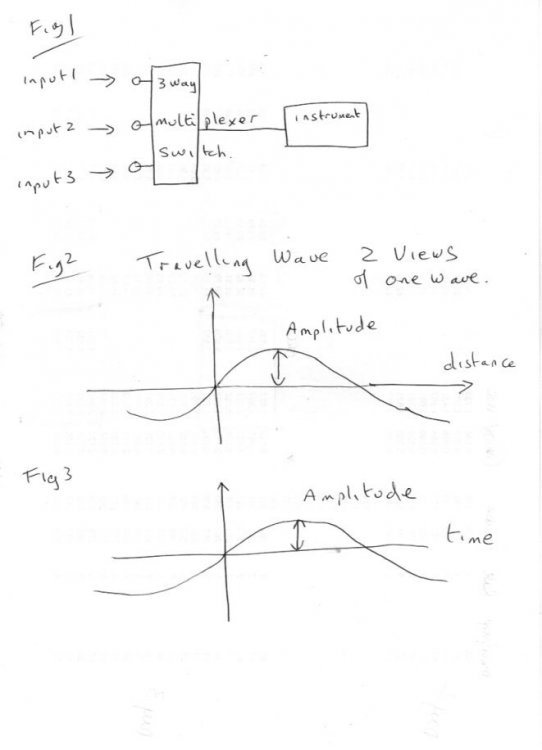
This is what I do not understand, I am hoping studiot will continue working with me so I can fully understand what happens when waves are combined. I apologize to all in advance, I am a slow learner. Thank you for your confidence. That is entirely possible for an instrument to be switching and for it to be confused if it is not properly set up. The technique is used extensively in electronics and is called multiplexing. There are quite a few variations. The old fashioned FM radio broacasts as well as TV used what was called frequency or phase division multiplexing. More recently the Internet runs on something called time division multiplexing. It also employs route division (space) multiplexing The idea is best illustrated by a diagram. Basically signals from more than one source are connected through a switch which cycles through each signal source for a fixed period then moves on to the next and so on round the cycle. So the instrument sends or displays or measures or whatever, the signal from each source in turn and then moves on to the next until it has read them all. Then it starts again round the cycle. That is shown diagramtically in fig1. But enough of this digression - back to waves. Good on you for looking up travelling and standing waves. The sine wave I posted is a travelling wave, but there is a twist to the story. A wave connects time and space. I won't post the 'wave equation' for now but let us put some flesh on the bones of my sine wave. I didn't label the axes for a particular reason, I will now explain. A wave shows the variation of some property or quantity in time and/or space. This variation is periodic in nature which means it repeats over and over again indefinitely. The quantity always remains finite - do you understand this ? So if we plot a graph of this quantity as the vertical y axis, it is often called the amplitude against either time or space as the horizontal axis we will see the sine wave I posted. The shape of the wave is called the wave function, in this case a sine curve but it could be a different repetitive curve that always remains finite. So now we have two plots Amplitude against space (distance) Amplitude against time. These appear in figs 2 and 3 And waddaya know ? They are both the same. An observer looking out over the wave crest cannot tell if he is looking out over time or space. This is a most remarkable characteristic. Next time we will combine some waves to produce some interference and standing waves.