studiot

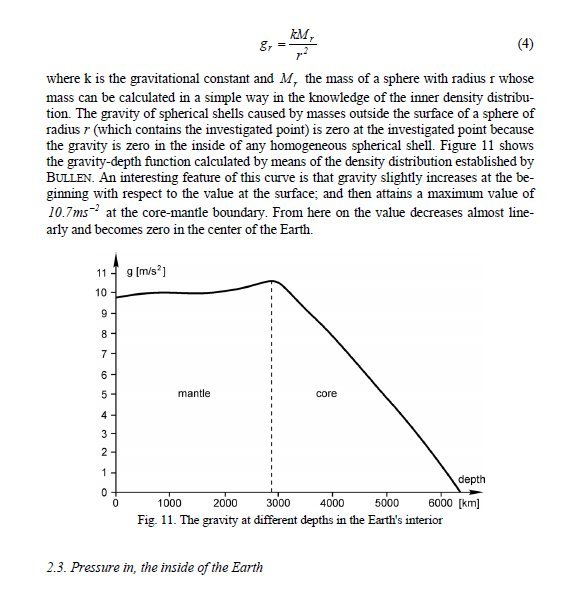
Has no one looked at the paper I linked to it is a free pdf download. ? But too long (and against the rules) to fully reproduce. However I was suprised how much difference the different densities of mantle and core make to the variation of g.

Sika publish pretty comprehensive documents safety (15 pages) https://gbr.sika.com/dms/getdocument.get/5fad402e-5b88-3470-a2eb-87bf1b31ef0e/Sikaflex221.pdf The section on personal protection is interesting. Have you read it? and use (12 pages) https://usa.sika.com/dms/getdocument.get/2bc4a3da-b682-3ff9-bbe0-e5b73f217550/General Guidelines_Bonding and Sealing with Sikaflex_v5-2018_EN_US.pdf

Good stuff, +1. However you missed the zero dimension. In one dimension the 1 dimensional differentiable manifold is the interval [a , b] , a function of one variable f(x) and the boundary comprises the two points a and b. so the theorem says that [math]\int\limits_a^b {df = f(b) - f(a)} [/math] IOW the Riemann integral. The link to time (I am trying to avoid the word connection) is that in space-time, time is somehow one of the variables in the manifold.

Surely N is not " the number of molecules",, but " the number of molecules between r and (r+dr) ? In other words surely N is a function of r and increases as the gas layers become more dense ? Haven't you treated N as a constant in your integration? I look forward with interest to your integration of g/T, both of which are also functions of r. I looked at this analysis which is a standard fluid mechanics/meteorology solution. I did not pursue it because there are direct measurements that support the assumptions it makes and provide many calibration points for the constants. As a matter of interest, this article is a bit old but contains estimates of the variation of gravity, temperature and pressure in the rocks as functions of depth. https://www.researchgate.net/figure/The-pressure-at-different-depths-in-the-Earths-interior_fig12_228377528 Look at pages 12 through 17 in particular

Thank you for the amplification. Yes of course they can. Knowledge of this goes way back a simple example being energy methods v force methods. Fourier transforms are another. Another way of putting this is that much of our physics is really just drawing glorified graphs. And as we have noted before, one can always plot the same geometric result using different axes (domains). Hopefully you have heard of Synge. He was a famous 20th century professor of Maths and Physics at Dublin (died in 1995) who did a lot of work on Mechanics and Relativity, amongst other things. The hypercircle method combines two infinite dimensional function spaces (domains) to generate a boundary hypercircle to/of solutions to a physical situation when on F space is mapped to the other.

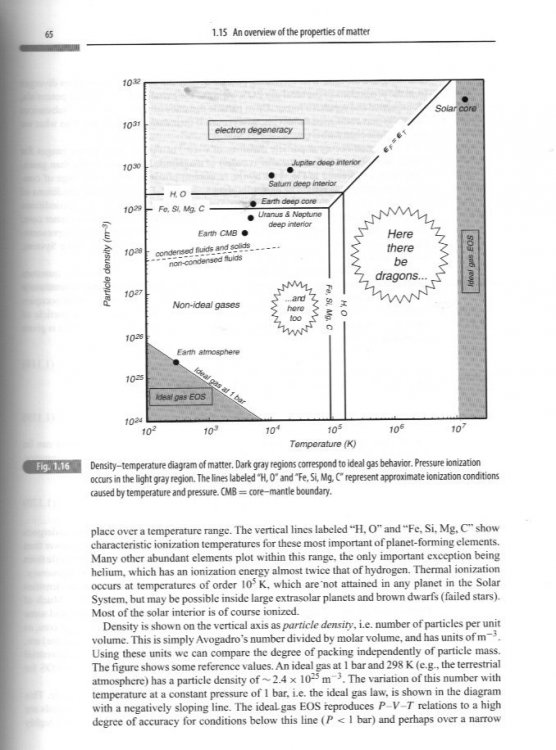
For those who are interested here is a chart of pertinent physical properties from Thermodynamics of the Earth and Planets by Douce (Cambridge University Press)

Obviously I must have misunderstood you, perhaps you would like to clarify ? (Particularly FTC, ADS and CFT ?) I thought that Gauss' theorem was a link between the bulk physical theory and a field theory on the boundary ? Are we not talking about solution methods to the 'boundary value problem' ? Have you come across the method of Prager and Synge linking the geometry to boundary value solutions "The Hypercircle in Mathematical Physics." ?

I wasn't going to post this before I had fin ished working on it but here is a summary. Please ask if there is anything you don't understand as it is not really beautiful enough for formal presentation. However this is not a competition so any suggestions as to the form of rho(r) is welcome. Edit I thought I posed this last night but obviously skipped the submit button. Note the correction to Martoonsky's original posting. It seems that we are all converging to a similar solution. My idea of a power series was to represent P(r) as a power series or inverse power series. This would then be multiplied through by the jr gravity term and allow easier term by term integration. The downside is that there is only one calibration point for the constants at r = R. Perhaps MigL's equation could help, I have not heard of this, cosmology/astrophysics is not my bag. +1 Have you any references MigL?

Yes I might try that, I wanted the little circles round the integral signs. I do remember when I first came here the site's latex couldn't display the triple bar identity sign or the proper limits of a definite integral or summation sign. At least these have improved.

Last time I tried to write this out here, the site's crappy Latex defeated me. I will have another go sometime. It really is a wondrous thing that for many situations that actually concern us all the information about what is going on inside a closed boundary is available by just considering the boundary. But yes this is tied up with Gauss, Stokes and Green's and Riemann. Even better there is a digital or discrete version that is in great use as boundary elements v finite elements.

Indeed there is. It's called the fundamental theorem of calculus.

Man you have waay more click stamina than I do.

@Winterlong Do you need moree explanation of this ? Markus loves tensors. 😉

Yes you seem to have understood exactly what I am thinking. The gas in the tunnel gains internal energy from the pressure of the gas above it (at r greater than its own). You cannot change the internal energy of a gas without changing its temperature so it also heats up. Heating up is a very important point since the air entering at the surface is already nealy 100o above critical. From then on the compressibility v pressure is fairly linear. Adiabatic, semiadiabatic insulating non insulating walls, the gas will also gain some heat from its surroundings -- more heating up. I was not thinking virial or VDW when I mentioned power series solutions. I was thinking about the aerostatic differential equation with a differential radial element dr. I was thinking of a power series solution to this equation. It is this element which is confined round the tunnel perimeter, but subject to compressibility radially. We thus have to consider the radial compressibility and have a choice isothermic or adiabatic ? I choose isothermic because I consider this differential element to be all at one temperature.

Yes they are. My model is isothermal so doesn't depend on adiabatic walls. The North Atlantic Gyre does not depend on time either, but there is still a dynamic equilibrium with coldwater descending and warm water rising.

I did not say it was silly (or clever) . I don't know where you got it from, whether you dreamt it up or saw it somewhere. The point is that your original statement is a compound statement of two mutually incompatible simple statements. That is the reason you have reached a 'paradox'. Such a technique is a recognised method of mathematical / logical proof /disproof of a proposition, But you don't seem to want to write the last line Which is "This results in a paradox, therefore cannot be." I glad that the discussion has elucidated many other points for you however.

Yes but that is not all. The whole question was originally too short on detail. It never was a practical proposition. So yes we can allow superstrong adiabatic walls. But don't forget that the real Earth has a molten nickel iron core of some sort. Drilling a hole into this will produce the all time great gusher of a well. So this thought experiment must allow some magic to be allowed to proceed. As a matter of interest we have produced pressure in excess of those at the centre of the Earth but only in a so called diamond anvil. I am using constant Earth density (not gas density in the tunnel) as a first stab. That should produce useful ball park information. That cannot possibly be because heat must be transported down the temperature gradient. You don't need a source of air. I said circulation cell and countercurrent flow. They can occur in straw. Both these are already known to operate in terrestrial processes. The helical generator version is the closest model to the Earth's dynamo we have within the core.

There must be. No vacuum either. You would get countercurent flow of colder air, just as you do in the atmosphere more generally. The system would most certainly not be in equilibrium, any more than the atmosphere or interior of the Earth is. Stars are constantly ejecting high temperature material. Yes I think it is a good idea to develop this in stages, refinign as a result of information gained at each stage. Because you tunnel goes right through the Earth, the function P(r) must be symmetrical about the centre ie an even function. So a power series expansion would contain only even powers. My model so far has a product of two functions of r so involves integration by parts. Are you up for that? I will be interested to see what temperatures you come up with with a static solution.

Ken, +1 for the insulator idea. Conventional meteorological models convert the compression to temperature to perform the integration. But they also mostly consider gravity constant. Apparently this assumption makes less than 0.5% difference in the atmosphere (Yuan 1970) I am not convinced the air would reach plasma temperatures. Even without the Earth's rotation a plume of hot air would issue from the ends of the tunnel. The rotation makes it important to specify the direction/position of the tunnel.

Within the Earth, the gravitational acceleration increases linearly as you move from the centre to the surface. So this has the form g = jr, where j is a positive constant. An interesting side effect of this is that if you dropped a capsule into one end of the tunnel it would execute SHM about the centre. Of course, above the Earth g diminishes in accordance with the nomal inverse square law. But you don't need this. I am working on the density ATM, so these relationships can be combined

Gosh I though chickens came from KFC. Silly me.

There seems to have been a slip of the keyboard there it should, of course be a + b = 6 and a + b = 7

Yes this is your basic problem, right at the beginning. The basic fallacy is trying to combine two incompatible statements and preceeding from there. That will always end in tears many famous paradoxes and other trick questions can be resolved by realising this. Mathematically it is rather like a lazy teacher who wants to go off for a smoke so he sets the class the following problem and offers a prize for the solution when he returns. Sove the following simultaneous equations for a and b. a + b = 6 a + B = 7 You said The ship is travelling in the universe The ship is 10 m long. So the universe cannot be '1m long'

I have done quite a bit of both acoustic emission testing (your technique) and (ultra)sonic propagation testing over the years. It is still an up and coming technology. We still have much to learn, there have been good successes as well as spectacular failure with these techniques. https://www.astm.org/DIGITAL_LIBRARY/STP/PAGES/STP15782S.htm A technique allied to this is called acoustic signature analysis. In my day processing the huge amounts of data required was a difficulty, as was calibrating a measuring device using these principles. Neural networks are a modern method of attacking the data processing aspect, the second one still remains. I suggest you look around the existing subject more widely as the applications are already legion, but there will be a ready market for genuinely better equipment in this field. As a liquid velocity meter, how is your gadget affected by water quality eg suspensed material in the water ? Ability to distinguish this could be a useful variant if it can provide an alert to contaminants in the piping.

In Physics ? Interestingly in German the terms im kleinem : often translated from german textbooks as in the small and im grossen : often translated from german textbooks as in the large are used for locally and globally In Mathematics the term local <some property> applies in some neighbourhood of a point but not for all points in the entire set. That is reserved for global, where the property may be applied to any and every point in the set without restriction. A slight point here arises because strictly the term neighbourhood may apply to the whole set as well. So really local on its own is incomplete. It requires a statement of restriction for that.