studiot

Looks like part of some form of double flask reflux condenser. Here is one for essential oils preparation.

Are you serious or is this just an attempt to stir the pot ? Try googling accidental discoveries ie those with no prior theory eg https://interestingengineering.com/15-accidental-science-discoveries-that-changed-the-world There are many many important examples where observation preceeded theory. eg X rays, radio-activity, cosmic background, penicillin, .........

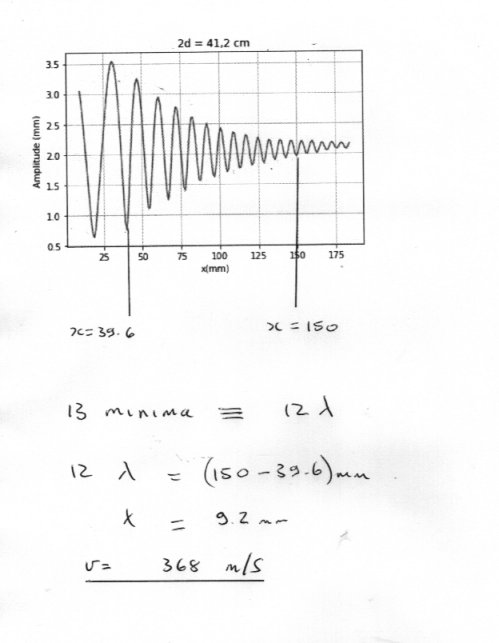
Include a “d” term for both and it may make more sense. It will cancel, of course. The change in the path difference is entirely from the upper path. Yes perhaps I was making things too complicated. @henk jan I really think your results are OK. Have you counted peaks correctly ? I make your estimate of the sound velocity 368 m/s If you look carefully, there is a big variation in apparent wavelength close to the mirror and a weak waveform at far distance as the pattern dies away. So I have chosen the 13 minima from the middle section to provide an average over 12 wavelengths. Also how accurate do you think the frequency of your sound is ? Does this now help ?

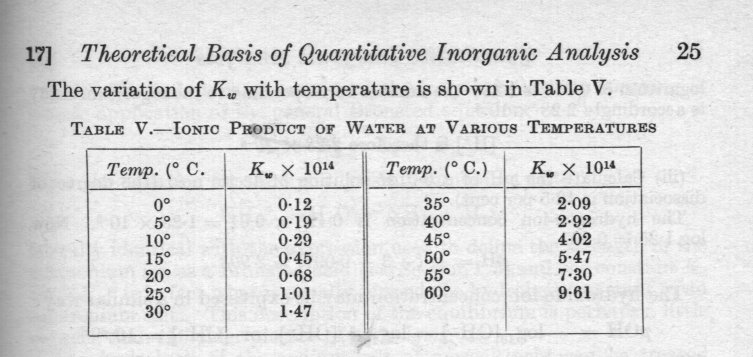
Since this is all you seem to want to know, the dependence of pressure is negligable for range of pressures encountered outside specialist facilities. Here is a table of dependence on temperature. As can been seen this varies by a factor of about 100 over the range 0oC to 60oC Both temperature and pressure dependence are experimental facts, which is why everyone is talking about tables of data. I would suggest looking in the Chemistry or Science reference section of your local library. Since you are in Australia, they will probably have the latest copy of Kaye and Laby, Tables of Physical and Chemical Constants from the UK National Physical Laboratory or Lange's handbook of Chemistry or The CRC (rubber) book Rather smaller books of tables prepared for national schools and colleges, such as the Nuffield one or SI Chemical Data by Aylward and Findlay (Wiley) Or yes you could ask Google. But you need to go right back to my proforma standard equation A + B = C + D to know what to look for. You would also need this equation to use the information correctly, as exchemist has already indicated. There are four different possibilities Strong acid + strong base Strong acid plus weak base Weak acid plus strong base Weak acid plus weak base. Each of these leads to a different equation, which must be handled appropriately (differently). The last one is often used in a simplified form called the Henderson - Hasselbalch equation, (which itself has two versions) especially by the life sciences (biochemistry etc) where is was originally stated. So you see there is not one equation but getting on for 10 different ones depending upon circumstances and complexities and where my express version was heading. I am sorry you didn't like it as it involved me in substantial work on your behalf.

Is there a phase change for sound ?? Yes for light

I suppose this partly depends upon what you mean by. 1) A standard academic establishment 2) A standard research establishment 3) Political. Society is far more complex than you perhaps suppose so what are you counting in and what are you counting out ? Since you are new here perhaps it is fair to warn you that you have a total of 5 posts allowed in your first 24 hours. So use them wisely. After this day you can post to your heart's content.

How is this correct ? What two waves are interfering to produce the nodes and antinodes ? The sound mirror is at position a or position b, but not both at the same time so how can these interfere ? Surely the difference in path length is between the direct wave ie d (if you must but I still say 2d is easier) and the indirect wave which is reflected off the sound mirror. Now exchemist has asked a very good question. What is the length of the indirect wave ? Well is it just the distance from Bron to the reflector plus the distance from the reflector to Ontvanger ? Or does any phase change at the solid boundary (metal sheet) make a difference ? The article I posted for you describes this as does the sound wave section in Wikipedia, which you should be able to get in Dutch. https://en.wikipedia.org/wiki/Reflection_phase_change If so what difference ? Bear in mind that a phase change can be related to a distance change via the wavelength. Because you are measuring distances you should be working in terms of wavelengths. Remember that a phase change of π (distance = λ/2) represents destructive interference ie a minimum and a phase change of 2π represents constructive interference (distance = λ)

Perhaps that's why my carrots from the supermarket go black so quickly, I often wonder what they wash them in.

Excellent, thank you. +1 I suggest that you use 2d for the distance between Bron and Ontvanger as this makes the maths simpler. What formula are you using for path length difference that is what is the relation between x and d and path length ? and what does the plot of intensity against x from your machine show (can you show a picture ?)

A proper (but short) description of your experiment and calculation would go a long way to explaining the issue. Until that happens we are just guessing blind.

Thank you for coming back to discuss. No the parallel was definitely not that I though your posts confusing. Actually I did not find what you said confusing, just that it did not seem to lead me anywhere. To explain my sugestion about the book. I reckon he was thinking 'ouside the box' and you are perhaps doing something similar but having trouble crystallising your ideas and setting them down in a presentable order. They may or may not be good ideas but until you can express them understandably to others they will remain undisclosed. You should not think of Mark Levi actually proving Mathemtics in a way acceptable for a formal maths text or treatise. But that he can demomonstrate processes in the natural world that follow them helps some people and shows there is a connection beyond mere symbolism. And he has some very interesting (to me anyway) ideas on this. I think he overdoes Pythagoras, but demonstrating the Gauss-Bonnet Theorem by Physics is quite something. Out of interest I find Stanislaw Lem very confusing. My wife and I once cooperated in a translation from Hungarian to English of some of his works. Personally I am not very interested in number theory but I was intrigued to find out more about this emboldened claim of yours I am also wondering if you are grappling with ideas of algebraic geometry ( & topology). These were introduced when it was discovered that the basic ideas (elements) of point, line, plane and hyperplane do not fully cover or describe (since 'cover' is a special word in maths) even the extension to 2 dimensions let alone 3 or more. Some additional basic elements were required. And one type is based on a triangle.

Something seems to be lost in translation here. How is a pH of 8.6 acidic ? More to the point is this all not off the original purpose of making acids for agricultural purposes of modifying soil not making a bactericidal wipe or spray? I say this because I looked round at 'anolyte' and found some western companies offering hard to believe claims without any evidence, as well as some eastern european (including russian) sources. So it would seem to me that that particular subject deserves a thread all of its own as any acid of this type has no known agricultural use.

If you require industrial quantities then it would almost certainly be cheaper to buy industrially.

I only posted here because you introduced your theory of limits here so our discussion is about pure mathematics and the thread is about something else entirely. So that other mathematicians here can get the chance to see this I am going to ask the moderator to split this thread so that the maths discussion can proceed separately. Meanwhile I would expect a straightforward definite and complete answer to a relatively simple question in support of such a claim about limits, not a lot of waffle and hand waving about other functions. If you need guidance on TEX or Markup I suggest you ask in another thread or look for some as there are already plenty or ask a moderator.

Did you say the limit in your definition is multivalued ? Note I haven't said that you are correct or incorrect. According to conventional real analysis this limit does not exist. But then neither does infinity. And yest we can handle infinity in the extended real number sytem. So I ask you again please state mathematically how your system handles this limit if, as you claim, it does so. In other words how does your set of shifts map to the real number system ?

Markup works reasonably well here but there are unfortunate wrinkles you need to follow. As a matter of example how would your system handle the limit of the following real valued function? [math]\mathop {\lim }\limits_{x \to 1} f\left( x \right):f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1 - x} & {\left( {x \le 1} \right)} \\ {2x} & {\left( {x > 1} \right)} \\ \end{array}} \right\}[/math]

To answer your question is is instructive compare Einstein and Newton. In his early career, Einstein did not get on well with the academic establishment so was forced to work part time by himself on his own subjects. Fortunately he had a sympathetic boss where he worked in the Patent Office. It was here he used the experimental results of others, for he was a theorist, combined with the quite extensive maths and physics he already knew, to develop his Special Theory of Relativity. It was called special, not because it was the best, but because its application was stricltly limited. At all times he was a Physicist who used the maths developed by others. He developed no new maths of his own. He was, however, very keenly aware of the limits of his special theory and wanted to extend this further in Physics. Here he was helped by some eminent mathematicians of his day. Minkowski and Weyl amongs others. Here to he created his famous shorthand notation for some of the nw maths they helped him adopt. This was the Einstein Summation Convention. Not new, but some say easier to work with. And here he did indeed extend his special theory much much further to the genral theory we know know. Elsewhere, and this is how he gained his Doctorate and Nobel prize, he used existing maths to revise and extend some statistical Physics on Brownian motion and what we now call Bose- Einstein statistics. On the other hand, Newton not only introduced a wide range of theoretical physics, he was a great experimenter and also had to invent most the maths he needed to write it all down. He did not rely on the maths that existed in his day, although he took full cognisance of the work of others around his time. He, like Einstein and many other great scientists, was aware of the limitations of his theories and thought deeply about them. But he did not necessarily strive to overcome them. He did, however invent the mathematical method of successively better and better approximations that we use today in so many of our calculations, under the general heading of 'Numerical Methods'. does this help ?

I doubt if that is the question as written. How many mL are needed to dilute 100 mL of NaOH ? How many mL of what wine ?, whisky ? ....? Secondly ask yourself "How much original solution are you trying to dilute ? Well it appears to be 100 mL. In which case you haven't finished the calculation since you have only only diluted 20mL of the stuff. Since this is homework I will let you finish but just observe that you are on track to obtain the right answer. Here is a comment. The equation C1V1 = C2V2 is quick and dirty and much bandied about, but does not always work directly. And you need a volume. I have seen many Pharmacist students come to grief trying to rush a calculation with this formula. Here is an alternative that always works, and works whether you have volumes, % or weights and concentrations can be used in any form, so long as consistent (ie the same) units are used. It works for mixing creams and so callled 'alligation' questions. It works when the % of one component are 0% or 100%. In short it works for all forms of mixture. If you like this we can work through how easy it is to get the right answer to your question with this method, once you have finished yours.

Again NO. You have been told at least four times now that this is not true. However until you understand how to calculate the pH of pure water with nothing in solution, you will never be able to understand the next step of how to calculate the pH of a solution. If you have a sample of pure water, it does not matter whether this is 1mL in a pipette (or even 0.1mL) or 1 million gallons in a tank the very small proportion that is ionised to H+ and OH- is the same. Do you understand this ? I thought that was pretty clear. They say it takes a good teacher to spot what a student has done wrong and put that right, rather than just say "you have done this the wrong way - do it this different way" +1

That wasn't quite what I (or exchemist) said. There are many constants in Science that can only be determined by experiment as we have no deeper theory to derive them from. These include the mass of the electron, the acceleration due to gravity, Avogadro's number, the thermodynamic constant gamma to name a few and show how widespread they are. However once they have been measured, they can be used in conjunction with theory to determine other desired quantities. The ionisation constant for water is just one of these. Soulubilities (solubility constants) are very similar. That is also why engineers and scientists have extensive tables of Physical and Chemical Constants and other data. I posted a lot of material Look carefully again at the part where I started to to develop the pH scale and ask questions about what you don't follow.

I think you said you are studying on your own, not following any formal course so I will lay it out in some detail as you do seem to have got in a pickle. No that is not the equilibrium equation so let us start from there. For any chemical reaction we start with reactants say A and B and end up with products say C and D. We write this as [math]A + B \leftrightarrow C + D[/math] Note there are no square brackets in the chemical reaction, but there is a double headed arrow because every chemical reaction is really two reactions one going forward from reactants to products and one going in the reverse direction. Now every chemical reaction also has a speed or velocity. In general this speed is proportional to the concentrations of the reactants. So for the forward reaction (note the single arrow this time) we have [math]A + B \to C + D[/math] With velocity Vforward given by [math]{V_{forward}} = {k_{forward}}\left[ A \right]\left[ B \right][/math] Where kforward is the combined constant of proportionality for both reactants. Note also we have now introduced the square brackets to represent the reactant concentrations which we said the speeds were proportional to. Similarly we can create the corresponding equations for the reverse reaction (note the reversed arrow) [math]A + B \leftarrow C + D[/math] and [math]{V_{reverse}} = {k_{reverse}}\left[ C \right]\left[ D \right][/math] Now we ask what chemical equilibrium means. It means that the speed of the forward reaction equals the speed of the reverse reaction so there is no overall change in concentrations of reactants or products. [math]{V_{forward}} = {V_{reverse}}[/math] Which may be written [math]\frac{{{V_{forward}}}}{{{V_{reverse}}}} = 1[/math] Substituting in the expressions for these speeds, [math]\frac{{{k_{forward}}\left[ A \right]\left[ B \right]}}{{{k_{reverse}}\left[ C \right]\left[ D \right]}} = 1[/math] Rearranging to form the ratio of proportionality constants [math]\frac{{{k_{forward}}}}{{{k_{reverse}}}} = \frac{{\left[ C \right]\left[ D \right]}}{{\left[ A \right]\left[ B \right]}}[/math] We arrive at the equilibrium constant for this particular reaction [math]{K_{equilibrium}} = \frac{{{k_{forward}}}}{{{k_{reverse}}}} = \frac{{\left[ C \right]\left[ D \right]}}{{\left[ A \right]\left[ B \right]}}[/math] Note that because of the rearrangement the products are on top of the fraction and the reactants on the bottom! This leads to the mnemonic rule [math]\frac{{{\rm{Products}}}}{{{\rm{Reactants}}}}[/math] When using these constants. OK so to use all that for the reaction which is the self ionisation of water. First write the reaction [math]{H_2}O + {H_2}O \leftrightarrow {H_3}{O^ + } + O{H^ - }[/math] At this point I am going to cheat and simplify because using the hydroxionium ion may be strictly more correct, but it complicates the maths so I will just use the single hydrogen ion and single hydroxyl ion, as I want to proceed to pH issues. [math]{H_2}O \leftrightarrow {H^ + } + O{H^ - }[/math] So we have lost B from the reactants. So the equilibrium constant for this equation is [math]{K_{equilibrium}} = \frac{{\left[ {{H^ + }} \right]\left[ {O{H^ - }} \right]}}{{\left[ {{H_2}O} \right]}} = 1.8x{10^{ - 16}}[/math] Note these are always experimentally determined values. They cannot be found from theory alone. Now the concentration of the water in dilute aqueous solutions is constant and given by [math]\left[ {{H_2}O} \right] = \frac{{1000g/litre}}{{18g/mole}} = 55.5moles/litre[/math] This gives us a new equation [math]\frac{{\left[ {{H^ + }} \right]\left[ {O{H^ - }} \right]}}{{55.5}} = 1.8x{10^{ - 16}}[/math] or [math]\left[ {{H^ + }} \right]\left[ {O{H^ - }} \right] = 1.8x{10^{ - 16}}x55.5 = 1.0x{10^{ - 14}}[/math] Which is the value you have come across and is called the ionic product constant for water This is given the symbol Kw to distinguish it from the equilibrium constant. [math]\left[ {{H^ + }} \right]\left[ {O{H^ - }} \right] = 1.8x{10^{ - 16}}x55.5 = {K_w} = 1.0x{10^{ - 14}}[/math] Noting further that the concentration of hydrogen ions must equal the concentration of hydroxyl ions we have [math]\left[ {{H^ + }} \right] = \left[ {O{H^ - }} \right] = \sqrt {{K_w}} = 1.0x{10^{ - 7}}[/math] So to pH It is sometimes convenient to take the logarithm (to the base 10, they are not natural logs) and for any X ( which could be a suitable concentration or constant) the p function of X (spoken pX all one word) is defined as pX = -logX So for our water pH = -log[H+] pOH = -log[OH-] So -log[H+] -log[OH-] = log (10-14) = -14 pH + pOH = 14 =pKw Therefore in a neutral solution or pure water pH = pOH = 7 You need to fully understand all this before trying to calculate the pH after introducing another substance. How are we doing ?

This can be true, but there's salt and then again there's salt. At home, we use sea salt for cooking and other culinary purposes. Looking at the label it says that the fine sea salt (table grade) contains added sodium hexacyanoferrate (II) as an anti-caking agent. The coarse granules meant for a grinder do not. Of course sea salt contains iodates (which are famous for yellow staining) and many other compounds. We have never experienced this yellow colour with any of our stainles pans - either those from Portugal or the UK. Rock salt comes in similar grades, but does not include the range of additional minerals that sea salt does. Some manufaturers artificially add iodine to rock salt to emulate the composition of sea salt.

All sounds like useful information. +1

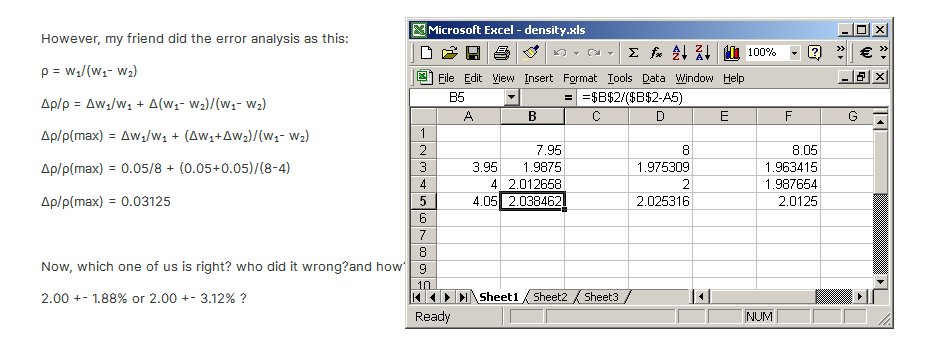
I make it 2 + 1.923%, -1.829% (brute force and Excel) You have come up against the difficulty of evaluating the partial derivatives of a function with a reciprocal in it. A good strategy in this case (as in most cases of small changes) is to remember the definition of a derivative [math]\frac{{\partial F}}{{\partial {x_1}}} = \frac{{F\left( {{x_1} + \Delta {x_1}} \right) - F\left( {{x_1}} \right)}}{{\Delta {x_1}}}[/math] Alternatively you can calculate the extremes of the function itself by spreadsheet, as I have done, or otherwise