studiot

https://en.wikipedia.org/wiki/Constantin_Carathéodory So consider the following process as outlined on the PV diagram where working fluid moves from state 1 to state 4 in three reversible stages or legs. Stage 1 -2 heat is accepted via an isothermal expansion at the lower temperature T1 and expansion work is therefore done. Stage 2 - 3 work is again done but no heat exchanged during an adiabatic compression, buit the work is of the opposite sign to that of the first leg. Stage 3 - 4 Heat is now rejected at a higher temperature T2 and work done in an isothermal compression to reach a point where the combined work of stages 2 and 3 equal that of stage 1. Thus exactly zero external work is performed, but a quantity of heat is transferred from a lower temperature reservoir to a higher temperature heat reservoir. So can you explain why this does not contravene the Second Law ?

There declares the man who also writes Is it? Never heard of it. in the same post. This was a far better statement as it leads to yet another version of the second law (The Chemist's version) Of course there were at least three different versions of the second law by those who originally wrote it and they are the subject of my first line of enquiry. However since my kinetic line was so ill received I don't know whether to bother. The original three statements, which are the classical one's most used by Chemical Engineers contain an extra condition that is all to often forgotten, and you seem to have forgotten it this time. It is that condition that I wanted to discuss first, before going off down a kinetic/statistical track.

Yeah it is certainly a big project, with a capital B that will take a lot of work. I am genuinely worried about this idea that one thing sits on another. This is true for some things, but for most subject areas you need to know a bit of other areas to do anything. When you have developed the new subject a bit you often then find you need to/can develop the 'supporting' subject a bit further and in turn can progress the top one. That is how we learn mathematics (and other technical subjects). What did you think of my tiling v tree comment ? I note Ghideon's picture does some of that.

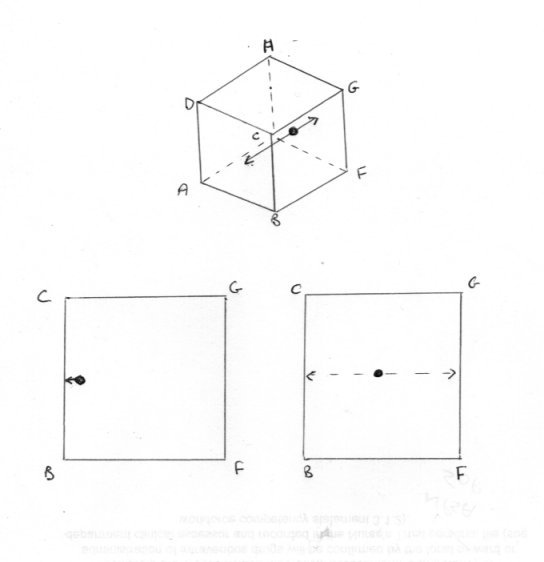
Of course it is possible. There are two lines of inquiry I was intending to pursue. Swansont raised one of them before I did so I will say something on that one first, although the better and natural order would be to consider the classical approach first. You did not reply to my question Which version of the second law are you considering ? There reason for this will become apparent in due course. So let us consider the activity of a single particle (molecule if you like). But let us simplify matters even further. Let us place the particle in a cubical box so that it bounces normally back and fore between opposite faces ABCD and EFGH. As a result of this it always follows the same track as in the third sketch. The consequences of this are that no force is exerted on any of the other four faces of the box. Now the thermodynamic pressure is defined as the average force of impact on all the faces of the box and being the same in all directions. Yet only two of the six faces experience any pressure force at all. Further when the particles is somewhere between faces no face at all experiences a pressure force. Pressure is an intensive variable, which should be the same throught the box or it is not defined. What about volume, an extensive variable ? Well the particle, being confined to its track, cannot access most of the volume of the box. So is volume a defined property either? Or is this a question of these Caratheodory microstates in his definition of the second law? Finally how can a particle striking a boundary wall be in equilibrium?

Thank you for introducing this interesting subject and welcome to ScienceForums. +1 I see the subtitle of this paper is "A Physics talk for Non Physicists". It was published in 2000 As such the author (who is an aged theoretical physicist) bends the rules to provide an analogy. Further he admits that the definition of mathematical complexity is not yet fixed. Although he does observe that Chaotic phenomena can arise in simple ones as well complex ones, he does link Chaos and Complexity inextricably. We do not do that these days. They are regarded as separate phenomena. Indeed the mathematical term 'complex' , as opposed to 'simplex' has been was originally introduced in one school of algebraic geometry and algebraic topology has developed in its own right. I don't agree that the specific folding example you highlight underlies all Chaos, for instance in the phase space of a system there may be chaotic regions and non chaotic regions. This will not happen with dough rolling as it (tries to) treat all regions the same. We have a curent discussion thread on aspects of Chaos here you might like to look at. Finally what is your particular interest in this subject, Maths , Physics or General?

I labelled my points firstly and secondly to help those who perhaps do not read postings carefully enough. What is the difference between accepting firstly in your own mind but saying nothing about It and ignoring it? Firstly is the key to the fluctuations you seem so keen to discuss. Secondly is about the status of these fluctuations. One thing that would be useful would be to state the version of the Second Law we are meant to be comparing the situations described to ? The issue is not to explain it but to ask how does it compare with the Second Law ? Consider this We rely on the observation that throughout the Universe electrons will be in the appropriate place and energy level for bonding and other activity (when required) despite the probability that they will be somewhere else at the appropriate time interval. When you compare the number of instances of such activity we have observed, to the probability of them doing something else must be incredibly small. Isn't the kinetic theory of gas molecules a coarser example of the same statistics?

Kit (sports) cars were all the rage in the 19060s/70/80s. At University I lost a friend to a serious motorway accident in such a car. The plastic body had shown one of the failings of plastic v steel and the body looked more like a draped curtain than a car body over the mounting points. Steel has superior creep properties to plastic. My brother lost a sailboat to another failing of plastic. Swelling in salt water. The early pvc insulation for house wirting hardened and became brittle after 15 years or so in service. So it is not all one way with super plastics, although some designer or other resurrects them every decade, having forgotten the lesson of the past. Are these newer plastics aging proof?

I did read it, perhaps not carefully enough. But I note that this thread has jumped around a good deal and plenty of additional material has been introduced but not in any coherent way. I would also observe that I only added a couple of very small points to swanson'ts original response, although I consider my point important. You do not seem to have addressed either of them. I now find myself in the situation of being puzzled as to whether to proceed with classical macroscopic thermodynamics where the typical version of the second law is being misrepresented by your references. System Entropy can and does decrease in appropriate circumstances. Or whether to look at the misapplication of statistics of your youtube reference. Misapplication is one word bullshit or baloney are others for those authors.

I don't know if you have heard of David Hilbert but he tried to do just this. The axiomatisation of Mathematics. You should read about his fate. https://en.wikipedia.org/wiki/David_Hilbert

Again some history (of mathematics) books publish timelines, These can also be a valuable source of information and inspiration.

A couple of things to add to swansont''s excellent post. Firstly Thermodynamics largely ignore the time variable. In particular it says nothing about how long a system will remain in a given state or how long it will take to reach that or another state. So these so called second law violations are 'instantaneous' and short lived, but the second law always wins on a time averaged basis. Secondly what makes you think these are actually formal 'states' ? Formal states have state variables that are properly defined. You cannot apply most of classical thermodynamics to improperly defined states.

When I was younger (the 1960s) I used to look forward to the Analog Science Fiction Annual every year. One year there was a short story called "Business as Usual During Alterations" Essentially some Aliens dropped a matter duplicator onto theEarth. At first everyone thought that would be the end of 'commerce and work and MONEY' But then some enterprising souls got a duplicator and started offering the service to "Duplicate your stuff for you to your requirements" And the good old American Dream was saved.

I think I get the general idea. +1 for ambition, I will remember to log on again in 3020 to find out how you got on. Meanwhile here are a few thoughts. If you have access to a library look at the contents pages of compendia of mathematics books. I have a couple by that name, one by Manzel (2 vols) and one by Meyler and Sutton. There is also the Princeton Companion to Mathematics and the Cambridge Encyclopedia of Mathematics. The contents pages should give you some subject headings to think about. Also some authors publish dependencies or dependecy diagrams such as "chapters 4 -7 should be read before chapter 11". though this is more common in Engineering than Mathematics. However such information from either subject could be very useful, as it shows what depnds on what. As regards the subject areas themselves I suggest you don't use the tree analogy. This reuqires that the 'branches' are separate areas or subjects. In truth there is considerable overlap and I don't thionk there is a single 'branch' that could stand alone by itself. There is considerable overlap, For instance although Geometry does not require measurement, you could not do Geometry without numbers even for shape and form. How else could your distinguish triangles, squares, pentagons hexagons etc? So I suggest you go for a tiled presentation, perhaps a bit more formal than in Ghedieons diagram (+1 for finding that). With suitable overlap or overlay you can sowh the interactions. Go well in your endeavour.

You should be able to get standard student note/handbooks very cheaply second hand. Look for Classical Mechanics B P Cowan Classical Mechanics J W Leech Statistical Physics F Mandl Statistical Thermodynamics Andrew Maczek All good intro notes for university

It is common practice (especially in schools) to state, somewhere near the beginning, "We will only consider statically determinate frames/beams/structures in this text." Sometimes a simple example of an indeterminate structure (such as a propped cantilever or a doubly cross braced frame) is shown as an example but not discussed further.

Your other points in the rest of your previous post bring out very nicely soemthing I often say. "We are really considering the geometry of graphs or plots of the connections between the variables." Now this has implications if some property of the graph or plot space is not mirrored by the variables. Here are my thoughts about fractal dimensions. Just take plane 2D for simplicity. 2D is 'made up' of points say x and y. Now Euclid tells us that a point has zero dimension. So are both the dimensions and the degrees of freedom of a fixed point or attractor zero ? Variables and definite connections between them (equations) allow a point to move about in xy space again matching dimensions and degrees of freedom to 2. Fractals are different. They have no equations to follow, they are procedural processes. Take the Koch curve and snowflake. The procedure involves taking points on the curve and moving them a small displacement in x and y. So points in the xy space are no longer on the curve in a finer scale or iteration of the curve. This process is different from taking two numbers on the number line and finding another number between them (continuity) since all points encountered are always on the line

Thank you, this is what I want to find out because it shows my example was not clear enough. Traditional examples of the difference between the physics and the maths are usually drawn from fluid mehcanics - I will think about it.

I would go along with this as a simple but solid opening statement. Thank you. The interesting question comes when you ask "Can a clear line between them be drawn ?" How do we include fractional dimensions of the space? whilst allowing only integer degrees of freedom (I can't see how any DOF can be fractional)

This reminds me of a long established tradition in English schools in answer to the question "Why do the English study English in school ?" In my day there was a subject called 'Use of English' Later in my daughter's day she studied 'Critical Thinking' The point of these was how to read and extract (useful) information from different pieces of english text and logically evaluate them. Of course the ambit was wider than Philosophy, but it always amazed me how clear thinking (university) graduates of English are.

I don't understant the connection, but Godel did discover a 'timeloop' solution to Einstein's equations. remembered reminded

Every schoolboy studying applied maths or physics learns the 'principle of static indeterminancy'. A formal system is the principle of static equilibrium applied to a structure. This says that the sum of the applied vertical reactions, the applied horizontal reactions and the applied moments must each be separately zero. This provides three equations for a structure. Some structures are statically determinate in that those three equations are sufficient to fully determine the reactions. For example a simply supported beam. For other structures those equations are insufficient for the determination, although the reactions must exist. Such structures are called statically indeterminate. For example a beam, built in at both ends.

Yes Strange's description of 'formal systems' is a good one. And whilst much of mathematics is embodied in formal systems some important parts are not. For instance the technique of iterative refinement is widely used in Science and Engineering. That is Have a guess at the answer or value you seek. Substitute in your guesstimate and see how close to the correct outcome you are. Refine your first guess and test again. Repeat until your guess matches observation to the required degree of accuracy. This technique appears in statistics as Bayes Theorem. Remember that in Physics well conducted observation always trumps any 'proof' or theoretical determination of a result.

Yes, the 'Law of unintended consequences'. +1 https://en.wikipedia.org/wiki/Unintended_consequences

Not just money but lives and livelihoods too. Read this https://www.bloomsbury.com/us/the-attacking-ocean-9781608196920/

The BBC has an ongoing series on medical matters. On the website there are a whole range of articles presented by doctors and researchers including links to proper academic papers and research trials to popular issues. https://www.bbc.co.uk/programmes/articles/3t902pqt3C7nGN99hVRFc1y/which-oils-are-best-to-cook-with I think many members will find something of interest in a browse around this part of the BBC website.