studiot

Where would I be without friends to put me right? +1

Good that you are still with us after all that squabbling. Please explain where you got those ideas post a link or reference. Because they are seditious. The whole point of Maths is that it is self consistent. But that does not mean that any part of it is complete ie tells everything. That is the point of Godel's incompleteness theorems - we will never know everything unless everything is limited. But we do not know and I do not believe that 'everything is limited'. If you like ? a bit of background about the Erlangen program and David Hilbert might help place Godel in context.

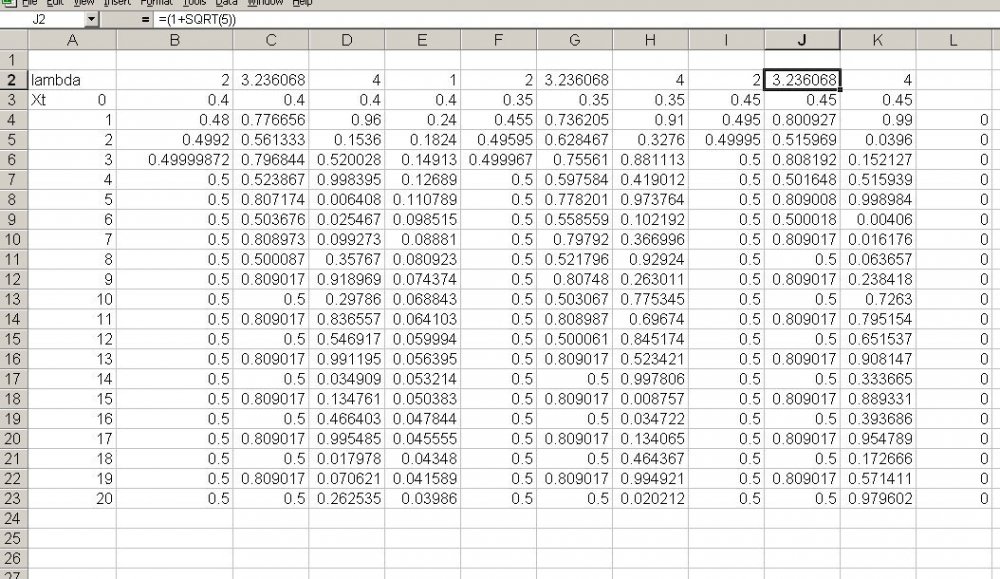
Here is the spreadsheet. I have calculated enough iterative values for different values of lambda {2, (1+√5) ,4} and starting values {0.35, 0.40, 0.45.} It can be seen that lambda =2 quickly converges, lambda = 4 displays the famous 'frequency doubling between two values' and lambda = 4 results in a chaotically varying result. I have appended the spreadsheet for anyone who wants to play with it. chaos1.xls

Hours in the tub? +1 for being the best washed member of SF!. Yes there is nothing at all incorrect about your analysis, but it does introduce some difficulties. Since you mention trajectories it then becomes necessary to define trajectory, path, locus, track, curve, trace and quite a few more terms. One of these extra terms is, of course, dimension - which we are working on in another thread. (aren't we) One of the problems with dimension and Hamiltonian formulation is that your equations only admit integer dimensions. A Mathematical definition of Chaos is "A system containing an attractor which is a fractal set." Fractals, of course, do not have integer dimensions, by their definition. Which introduces yet more definitions. The other problem with a Hamiltonian formulation is that it is designed for a material universe, involving energy and other material properties. A looser description is obtained by observing that such a formulation is a model (and a pretty damn good one at that) whose equations of constitution result in different behaviours when applied in different regions of the space involved (state space, geometric space etc). In some regions the behaviour is consistent and predictable by the equations in other regions it is unpredictable. We call this chaotic behaviour. Such behaviour is observed in regions 'controlled' by an attractor with an non-integral dimension - a strange attractor. But the space may not be material at all. I was going to illustrate that with a spreadsheet of the equation Xt = λXt(1-Xt) Which is just an equation involving numbers and not a Hamiltonian at all, representing nothing material in particular. Yet it exhibits Chaotic behaviour. New examples from all disciplines are being found. Scientists from all disciplines, not least Maths and Physics are working on this because it exposes (some of) the deficiencies and limitations of our current nice pat theories and will eventually lead us to new knowledge and understanding.

Many thanks to all who replied sor far. I do not think where the sticky is finally placed is currently all that important. I'm sure it end result will speak for itself and it will be linkable in any case. I do think, though, that the description and examples should be short enough, simple enough and clear enough for as many readers as possible (unlike Wikepedia). To start here is a possible description and example for my posher phrases When analysing a situation or a problem we can divide the known information into two camps. The Relations of Constitution refer to the Science (Physics ?) of the issue. These may be suitable Laws, Principles etc that must be obeyed by the system in question. Whilst these are often expressed as equations, they may not be which is why a more general term 'Relations' is used. For example neither the Second Law of Thermodynamics nor the Uncertainty Principle are equations, but inequalities. Even when we have equations (as in the worked example to follow) they may not allow solution of the problem or offer incorrect solutions. (There are an enormous number of such incorrect solutions to General Relativity) So we also need a second set of defining information, usually specific to the problem and often geometric in nature. Once again these often appear as equations but again they may not. For a specific problem these can be every bit as important as the Relations of Constitution since once you have solved the Science you still may not have the answer. This is also the difficulty any Theory of Everything must overcome. So all that sounds very pompous here is a plain old example to make things a bt clearer. A projectile is fired upwards at angle alpha to the horizontal with initial velocity V from the top of a 100m cliff, at a time t = 0. Calculate the time to splashdown in the ocean below. The Science tells us that the equation of motion required is h = V t sinα - 0.5gt2 Now this is a quadratic in t so it has two solutions. For alpha = 30o and V = 100m/s these are (nearest whole number) 12 seconds and -2 seconds. This is where Compatibility rides to the rescue since it places the Condition that t is greater than 0 (time is non negative) For the comparison of dimensions and degrees of freedom I was going to compare these for various plane frames (all of which have 2 dimensions but different degrees of freedom)

Thank you for that, it only just occurred to me and certainly shows the need to be careful with language. +1

My point remains. The equations you have written are hiding an summation which can become more and more intractable as i tends to infinity. Evaluating them for one or two single entities is one thing, evaluating them for a large number is quite another. And how exactly would you show say the North Atlantic Gyre (ie describe why it must be so and no other way) in Hamiltonian Mechanics, somewhere in the middle of the North Atlantic Ocean ?

@ahmet I disagree to this idea. because our keywords seems suitable: (* incompleteness) It seems I nearly lost a post when I went to dinner. Luckily the input editor here didn't loose it. I don't have Bourbaki, but here is an excerpt from Lang How does it help ? Can I also ask by circle do you mean ring? (I am particularly intested in the answer to thi since I wonder if there is a language difficulty)

Thank you for offering this however I think Bourbaki is way ouside the OP comfort zone. I was trying to interpret your response in the light of simpler mathematics. Of course there, division by zero is forbidden. However I think your response to Ghideon is the most appropriate since I also agree with Ghideon, on the understanding that the OP has a full stop in place of a comma I admit to being confused by your introduction of fancy mathematical notation, most especially the H notation, as used for Octonions. As far as I am aware the octonion ring is not a division ring with the necessary structure to include division by zero. The only possibly suitable one I can think of is a 'wheel' which has three defined operations, not two. Anyway as far as I know the OP is satisfied with the information.

Please post them anyway. (But only in outline form at this stage) The purpose of a sticky is to be useful to as many as possible for reference.

All I see is your statement 0+0 = 0*2, which is true since anything times 0 is still 0. What I don't see is a formal continuation of your line of reasoning to the end.

I don't know how you would develop a theory of turbulence or eddies from Hamilton- Lagrange mechanics but that is still besides my point. I know that an octopus does not swim with its arms, but suppose it did, using HL to discuss this seems to me like trying to model the trajectory of the tip of the 5th arm, when all arms are flailing to swim, from the Lagrangian of the overall motion of animal in the water.

When you finish the job, (ie write out the simplification) how is your conclusion reached?

This proposal is a result of my noticing how often certain issues crop up and was prompted by the following posts, which come from different threads. Before offering a draft version I would like to ensure two things. Assurance from the moderators that this is in order and will not lead to being called out as a blog. The opportunity for interested other members to participate in the drafting; I do not pretend to have all the answers. Maybe you should make article and make it sticky what dimension means in physics.. so they won't confuse it with sci-fi vision of other dimensions.. So I am suggesting two main areas for inclusion 1) Dimensions and degrees af freedom. 2) The Relations of Constitution and the Conditions of Compatibility and their implications for any proposed Theory of Everything (TOE). Please have you say here so that the final post can be transposed to the locked sticky.

I would just like to add in some words of caution here. Dimensions are often identified with degrees of freedom. Both have a (numerical) value. These concepts are not the same, although sometimes their values coincide. They are all too often confused with each other. Further it is important to identify the 'space' in which you are working - phase space, configuration space, geometric space and so on. The dimensions of these different spaces can (and often do) differ for the same 'system'.

Yes and no and yes , but I will come back to this. So to Eddies and Chaos. In a normal flow eddies form when there is a physical obstruction in the flow or the direction of part of the flow is diverted. This second option is what happened at the wing wall in the 'low sill structure' when the floodwate floded out to the side of the structure, beyond the wing wall. Here water is travelling sideways, ralative to the main flow and therefore being left behind. Eventually some of the water is flooding backwards in the opposite direction to the main flow. This formally contitutes the eddy and can form a complete loop of flow circulation. The same effect can be seen in the Texas manual I linked to around big obstructions like bridge piers and little ones like sticks held in the water. Kelvin's theorem tells us that these eddies come in pairs to maintain the non circulatory property of the main flow. This is well known in the phenomenon of vortex (eddy) shedding from the tips of aircraft wings and tail planes. The shed vortices alternate rotation direction. This is what I meant by Now it is tempting to think that the 'right conditions' might induce 'little eddies' as opposed to the 'big eddies' so far described. And that would lead to Chaos. Several factors mitigate against this, suggesting there is more to consider. 1) Big eddies are persistent and consistent in their orientation. Little eddies start and stop, and form in every direction. 2) Big eddies can form in both turbulent and laminar flow regimes, as occurred at the low sill structure. 3) It is normally found that turbulence start to occur below and above lower and upper limit critical Reynolds numbers. But more careful experiments , even some by Reynolds himself. show that these critical values can be substantially exceeded without turbulence forming. A final factor is that of specific energy. If the flow speed is altered slowly and smoothly the flow regime has time to adjust to the new conditions. But if the change is too fast the energy of the incoming flow builds up the specific energy in the water until it is greater than the flow can sustain. So the flow regime makes a sudden transition to turbulent flow, which has a higher intrinisc specific energy to accomodate this extra energy in the only way it can. This effect was used in the stilling basin of the low sill structure in normal operation to dissipate the energy of the emerging water. The purpose of the wing walls was to direct the water in a safe manner. But the water with the higher specific energy could wash away the material between the piles as a self regenerating process. The more it washed away, the greater the scour effect.

I don't follow. Does this mean you agree or disagree or just have not picked up on my point?

An apology for posting the Wikipedia link, I was in rather a hurry last night. The article was really too complicated, perhaps the result of a bit of showing off by the authors. In that respect the Mathworld article is better. Very often the axioms that are finally chosen (Note Wikipedia offers modern vesions and says that they are not Peano's originals) are a bit obscure and it is the theorems or lemmas we deduce from them that are what we actually want to use. In fact usually these theorems are properties we have observed and found useful so the axioms are constructed later to produce these theorems as deductiuons. The point is that in Mathematics to prove something means to show that it is consistent with the axioms. Since we have already shown that the theorems are consistent when we 'deduced them', this may simply mean showing that the something is consistent with the theorem(s). Anyway here are a couple of extracts from two books, one very famous, one very modern, that may help. They tell us about the something (numbers) that lead to the rules of arithmetic (the theorems we want) Both books are highly recommended. Unknown Quantity a real and Imagined History of Algebra John Derbyshire What is Mathematics Courant and Robbins

I suppose it depends what you mean by 'standard' There are two types of standard defined Line standards - as appearing on most ordinary rulers for drawing End standards - often used for metre rules for industry The difference is that the end points (zero and one metre) are defined between lines near each end of the rule or between the flush, squared off ends of the rule. So end standards are exactly one mtere long, line standards are a little longer. I am just waiting for my camera to charge to post a photo of the difference. In both cases the scales will be subdivided a Strange has already noted. So here is the picture The brass rule is an end standard. Note the countersunk hole for screwing it to a drapers or rope sellers cutting table. It does not come out very well but you can just see the ministry calibration stamped into the metal, between the 1cm and 2cm marks. This is the crown symbol and the date 10/1974 The plastic rule is a line standard for laying flat on a sheet of drawing paper.

The most important point to take from my post is that the mechanics of the ocean or the atmosphere or the Mississippi river is different from the mechanics of a swinging pendulum or a dripping tap or one dimensional displacements along a ruler according to a non linear equation, although common features as well as differences may be identified.

You seem to have some idea about axioms and seem to understand that axioms are what you start with (accept as true without question). Using these axioms you can then develop theorems (= very important results) (such as Pythagoras) and lemmas (less important results) What is not often said is that the axioms must be about something. These 'somethings' are given in definitions, which usually outnumber the axioms themselves. In your example (Pythagoras) in Euclidian Geometry there are 5 axioms and 23 definitions. The axioms you need for ordinary arithmetic are known as Peano's axioms https://mathworld.wolfram.com/PeanosAxioms.html https://en.wikipedia.org/wiki/Peano_axioms

What trajectories are involved in statics? Yet Chaos is involved in this subject, the simplest example being Euler strut theory. https://www.amazon.com/Stress-Stability-Chaos-Structural-Engineering/dp/0077072480 Of course there is also Statistical Chaos as well as Chaos in dynamic systems due to non linear action. The Dynamic Systems boys seem to have made a takeover bid for the subject however, although the first observed instances were not in Dynamic systems. Some outline additional thoughts here From this point of view it involves the system jumping suddenly to a different regime when some critical parameter is reached. But all of these examples are quite different from eddies and turbulence in fluid flow because the former are treating relatively simple rigid or semi rigid bodies as a whole. In fluids, of course, we have all sorts of different parts of the 'body' acting differently. In fact whole formal theories of 'complexity' have now been developed around this aspect of the subject. Many of the dynamical systems examples refer to chaos as apparent complexity I recommend this book to technical folks who don't want to wade through the heavy maths. https://www.amazon.co.uk/Scientist-Guide-Chaos-Penguin-Science/dp/0140145710 Here is a list of contributors and I will leave you with a definition from the London University Professor of Applied Maths

Yes and no and yes , but I will come back to this. I have done some investigation as I said it is interesting but the Mississippi is rather out of my Bailiwick. Anyway here is a list of references I have been looking at. http://onlinemanuals.txdot.gov/txdotmanuals/hyd/bridge_hydraulic_considerations.htm https://www.google.co.uk/search?q=failure+of+old+river+control+structure&tbm=isch&source=iu&ictx=1&fir=ftZcfe0bK17l7M%2CRRxDk-YnG3761M%2C_&vet=1&usg=AI4_-kTt_zi0s8YadwIFHcgXfndAvIoFOA&sa=X&ved=2ahUKEwjCiKyRmaLqAhVyVBUIHUVIDbgQ_h0wAHoECAUQBA&biw=1366&bih=646#imgrc=yJo1u-GB9q7rDM&imgdii=RRciLzxOFVVPIM http://www.americaswetlandresources.com/background_facts/detailedstory/LouisianaRiverControl.html https://www.mvn.usace.army.mil/Portals/56/docs/PAO/Brochures/OldRiverControlBrochure.pdf https://www.amazon.com/Beyond-Control-Mississippi-Channel-Americas/dp/1496811135 Please confirm which of the control structures is is currently causing concern and requiring concrete. The 1973 scour damage at the low sill structure seems well documented. I think an especial difficulty with this system is that water seems to be able to flow in either direction according to circumstance.

Hello Francis and welcome. The short answer is no Godel is not about statements we can prove, like yours, but statements we will miss out because we cannot derive them from our axioms. There is a really good introductory book by Raymond Smullyan about this called Forever Undecided Which is fun to read. I think a pdf may be available. Meanwhile here, what do you know about axiomatic structures in Mathematics?

Good subject to discuss. +1 However a few points. I would call this the use of the equals sign "=" not "equalities" because there are differences of usage. Equalities are only one use of the overworked sign. As you say for most people the context determines which one. Chemists (and others) use the equals sign as well as arrows to denote a process or the idea of "...A....leads to......B" Identities are not the same as equalities since x - 1 = 4 is true for one and only one value of x. [math]{x^2} - 1 \equiv \left( {x - 1} \right)\left( {x + 1} \right)[/math] is true for each and every value of x and is an identity. Strictly we should use the three bar symbol for identities.