Everything posted by studiot
-
What's The Point Of Calculus??
Yes this is a profound statement and very important in calculus and analysis more generally. This was why I said that dx on its own is meaningless. Yes a limit has one numeric value, if the limit exists at all. But this x can never = 0 statement is not right as it stands. We will come to a proper version in due course. But first some background, that will become increasing useful as things progress. Note the author says that Analysis is mostly limis and calculus, but it also includes stuff about functions, sequences and series which are necessary to move on from the algebra of quadratic equations. So let us start with variables and functions. You will be please to hear that we don't need the whole apparatus - That can take a whole semester by itself - just some of the bare bones. So variables. A variable is perhaps the most self evident word in Mathematics. It really does exactly what is says on the tin and no more. A variable is something that, well varies. More precisely it may take on many different values. And a numeric variable is a variable whose value is numeric. Your x is a (usually) numeric variable. So what values can a variable have ? Good question, note I may take on, not does take on. The question is incredibly wide since all we know is that the value of our variable is a number. So any value between plus and minus infinity will do. Enter the mathematical function to the rescue. The main part of a function is a rule or equation or other expression for obtaining (numeric) values. Other parts limit the actual numbers we are allowed to use. So the square root function excludes all negative numbers. That still leaves a lot of numbers available. Since x is a variable, we can expect most functions of x to also be variables. We put different numbers in and expect to get correspondingly different numbers out. An exception to this is called the constant function. You get the same number out, whatever number you put in. OK numbers in ; numbers out. We now have two variables, x and f(x) and we can start going places. I have said f(x) since you have used it. But I am now going to change to y = f(x), which is using the rule to define the function as most folks do. So the next thing to understand is that x and y or f(x) are two different types of variable. x is an independent variable, which means that we can put in any number we are allowed. y = f(x) is called a / the dependent variable because its value depends upon the both the number we put into x and the rule which generates y. Having swallowed and digested all this guff we know enough about variables so are now ready to examine all the types of the 'd' in dx. 'd' is called an operator. An operator performs some process on the variable it operates on - in this case the variable x. This is the reason for changing from f(x) to y. We can operate on y with 'd' to get dy. We will tackle that next time, but a question of you if I may. Another person in another forum has asked a very similar question. Have you any relation to Idon'tknow, elsewhere ? I want not mix up answers to each.
-
What's The Point Of Calculus??
I downloaded the third edition and I can't say I'm suprised you are confused if you are really using this book to learn the differential calculus. In particular my edition does not contain 'x' on page 7, 8 or 9. I asked you what you thought 'x' is because all those comments of yours that I have quoted suggest to me you don't understand this. It is vital that you do understand since 'x' is not a number. In arithmetic/algebra 'x' often stands for an unknown number that is to be determined In calculus 'x' is something else entirely and the book uses it in this way, but does not explicitly make this clear. 'x' is a variable. So that is where we should start. Do you wish to go on ?
-
What's The Point Of Calculus??
That wasn't the question you asked. If you are serious about understanding please try to pose you question simply but completely and without mockery. They someone here may be able to help you. I have no idea what you mean by "x can never be 1" Can you give a complete example that confuses you? I suggest you start by saying what x is.
-
What's The Point Of Calculus??
I doubt that many teachers would claim that Calculus is 'all about' anything. There are many calculi (the plural of calculus) and each has a different purpose. First there is the hint in the name 'calculus' = that which enables calculation. What you have described might be said as the introduction to what is known as 'the differential calculus'. This is indeed about change from one point to another. That point may be in time or place or connected to some other measurable quantity such as money or population or wheat yield or many other things. But there is so much more. There is 'the integral calculus', which is not about change but about summation. This is about what happens when you combine things together such as the energy you consume when you run 8 kilowatt shower for 30 minutes. Then there is the calculus of variations which is about minimising or maximising something. For instance what shaped curve will result in an object slding down it the fastest ie in the least possible time. This shape is known as a brachistochrone curve, if you want to look it up. MigL mentioned Newton - he allegedly solved this one is a day using calculus. Finally here is a very simple calculus, known as Russian Peasant Multiplication for calculating the product of two numbers. say 64 x 61 Write the two numbers down at the top of two adjacent columns Successively half the first column and double the second until 1 is reached in the halving clumn Strike out all pairs with even numbers in the first column Add those left in the doubled column thus 64 61 32 122 16 244 8 488 4 976 2 1952 1 3904 answer 64 x 61 = 3904 done without learning tables.
-
Phosphine detected on Venus
Back on Earth, combined Phosphorus is a contaminent in iron ore because it makes steel brittle. It is a highly reactive element There is a wealth of information in this article and its references, both chemical and biological. https://www.scielo.br/scielo.php?script=sci_arttext&pid=S0370-44672015000300331
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
The Staunton Defence ? Attempting to sidestep the question is inadequate.
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
So mathematics can define things those words he said cannot even come close to. Whereas you said it couldn't even be stated with mathematics which is false. Declaration is not demonstration or other form of proof. I would would be interested if someone was able to write down totally mathematically what Prof Swinnerton said. What do you think the mathematical statement for granite is?
-
Examples of Awesome, Unexpected Beauty in Nature
Look here for the connection to Science. https://books.google.co.uk/books/about/The_Self_made_Tapestry.html?id=Fz1RAAAAMAAJ&redir_esc=y or here for the comparison of how Nature does things v how man achieves the same objects. https://books.google.co.uk/books/about/Cats_Paws_and_Catapults.html?id=fdihsss71tAC&redir_esc=y
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
+1
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
So ?
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
No. Philosophers can think more widely than Mathmaticians, who are constrained by the rules. Philosophers can perform rational thinking, not available in Mathematics. BTW Newton was a (Natural) Philosopher (the old name for Physics). Here is my favourite example of what I mean, written by Professor Swinerton of Nottingham University. This deduction cannot be stated mathematically, but is a masterpiece of rational thinking.
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
There is a difference between logical thinking and rational thinking, the latter being far superior. Both good philosophers and good scientists should be able to utilise the additional capacity of the rational mode.
-
Open Learning Free Short Courses
The Open University (OU) lists over 900 free short courses in 8 categories. In the Science category you can look at Babylonian Mathematics, Chemical in drinking water, antibiotic resistance, Toys & engineering materials, working on your own in mathematics, telescopes and spectrographs to name but a few. Or you could learn/ brush up a new language in the language section Something to do in theses Covid times for all ?? https://www.open.edu/openlearn/free-courses/full-catalogue
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
I wonder, Does Good Philosophy v Bad Philosophy equate to Autobots v Decepticons?
-
Is there such a Thing as Good Philosophy vs Bad Philosophy?
I can't begin to imagine how such a discussion arose. Geodesy is the Science of the Measurement of the Earth. Astronomy is the Science of the Measurement (nothing else) of the Heavens. Astrophysics is the Science which includes the study of stellar processes. Surely there is nothing to argue about, we just use the definitions and get on with the meat of the real issue to hand.
-
question about balancing a reaction
This must be homework ? Is the reaction equation complete? Such a compound has a special name do you know what it is - It begins with the letter C
-
Youtube says the 2nd Law is Broken.
I had hoped we had returned to more normal forms of discussion. Since that is not the case I will leave you with the suggestion. Get a good English (or better Thermodynamic) Dictionary and look up the words 'piston' , which Mandl did not use, and 'partition', which he did. Both word have very particular and carefully defined meanings. go well and enjoy your stay in the Netherlands - I find it a very nice place.
-
Youtube says the 2nd Law is Broken.
Before this degenerates into another slanging match, let me step in here. Seth, you are mixing up macroscopic mechanical theory and microscopic kinetic theory. This link is proper statistics, you cannot 'mix and match' formulae from macroscopic and microscopic theory without doing this. No one is suggesting that in Mandl's diagram the system passes directly from state a to state b or from state b to state a. Either way the change is a gradual process, although there is a vast different of timescale between a to b and b to a. Consider first b to a There must be a first molecule that leaves side A and moves into side b Followed by a second, third and so on, although sometimes and sometimes only , two or molecules will exit the gap simultaneously. So , however fast or slow, the system must leave state b a bit at a time and move, a bit at a time, towards state a. A similar deduction may be made for the reverse process a to b. Now statistically the more particles there are the harder or less likely it is for most (all) of them to move from one side to the other, at or near the same instant. Your centre of mass argument is also suspect My single particle example negates that as its COM is always moving, but by Newton's laws, zero work is being done. Finally I said that Mandl's example was presented in his introduction to the second law. Like all good courses and texts he is up front about the difficult cases, where the simple theory is insufficient, but I also said he treats this later.
-
Youtube says the 2nd Law is Broken.
Now here is a thermodynamic question that all the textbooks in world will nothelp you with. However, even though (climate) conditions in Lagos mean you probably never experience this problem, as an experienced enginner, you may well be able to suggest a good way forward. When casting concrete in cold weather the concrete will suffer terminal damage if allowed to freeze in the first 24 hours. Suggest countermeasures to avoid this.
-
Youtube says the 2nd Law is Broken.
Absolutely not. That is even more obscure than ontology. Some examples of what I mean by Analysis : 1a) I hand you a container of a a pure gas and ask you to measure the % carbon in the gas. result 83.7% 2a) I ask you to measure the contours of an existing embankment (survey it). 3a) I point to the pavement of a concrete road leading into a nuclear power station or petrochemical complex ask you to measure the stength of the pavement concrete because I need to run plant along the road safely. Examples of Synthesis 1s) I ask you to manufacture a canister of a pure gas containing 84.7% carbon 2s) I hand you a set of plans and ask you to construct an embankment according to those plans. 3s) I ask you to construct a new concrete road with strength at least 6,000 psi to accomodate the plant I need to run along it. Does this make it any clearer? In each pair of cases which do you think is the more difficult task?
-
Youtube says the 2nd Law is Broken.
Sounds good. Does the stress here introduce a value judgment of a methodology based in its ontological classification (ie. what name you give to it)? I'll attempt to paraphrase Feynmann "If it disagrees with experiment, it's wrong". Conversely, all methodologies that agree like-for-like with measurements of the real world must be equivalently valid. In my experience ontology carries with it many hidden traps which makes me very wary. It's a branch of metaphysics and maybe best left to the theologians to play with. Not really, no, although ontology is too airy fairy for me. I am fond of pointing out the twin complementary processess of analysis and synthesis. Synthesis is largely practised by Applied Scientists and Engineers, (following the analysis of a problem) In my opinion it is more difficult to create something that does not yet exist (a dam a motorway, a chemical plant a harbour etc) to meet a specification than to analyse something that is. already there. I am worried about this since I picture say a red hot poker being thrust into a bucket of water as a line heat source or point heat source in any section. Surely this meets the specification of your point P , but generates motion and dispersion away from P not towards it ? Maczek (as it is spelled on the fron of my copy) is a very good and clear basic book I would recommend to anybody. He does not dilly dally with microstates like some but uses partition functions to the full. What is you opinion of partition functions v microstates ? You might also like to look into what Mandl (Manchester Physics series Statistical Physics) about your youtube issue. I think (please confrim or correct) that this is a description of it in his introduction to the second law. He goes on to split the probability function into two functions by , not the states themselves, but of the size of the fluctuations as a result of the N or n. He shows how the smaller N is the larger the expected fluctuations are from 'equilibrium'. Fluctuations sizes for a single particle are 'off the scale'
-
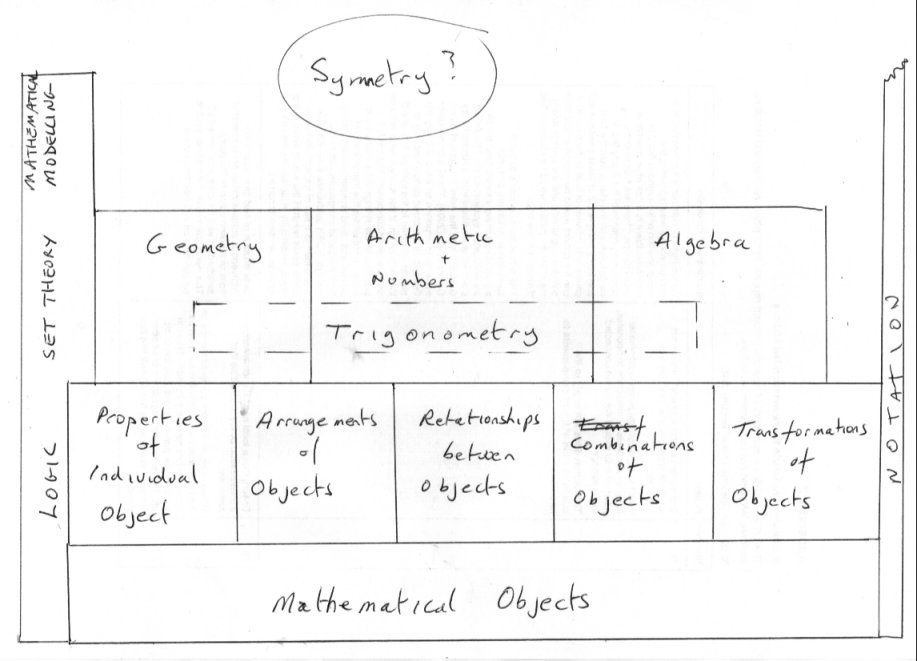
Attempting to create a generalized graph of mathematics
OK so here is the beginnings of my suggestion for one small corner of your map. What is Mathematics about ? What does it do? Well Mathematics is about mathematical objects and what we can do with them according to rules of logic. So what are mathematical objects ? Well they are objects like points and lines and sets and functions and shapes and angles and numbers and......... So what can mathematics do with them? Well it can describe Properties of objects such a symmetry, Arrangements such as an array (matrix object) , arranging points to make a square and so on. Relationshipes between two or more objects such as 10 > 3 Combine objects to generate another (different ) object such as 9x = iy) making a complex number Transform one object into another for some purpose eg taking logarithms Some of these operations are important when used to make the branch of maths called Geometry; Others support number theory and yet others support Algebra. So where does Trigonometry fit in? Well sinx is defined as opposite/hypotenuse and is a number so number theory comes in. Yet you can perform arithmetic operations such that sin2x + co2 x =1 so arithmetic is onvolved and again [math]\sin x = x - \frac{{{x^3}}}{{3!}} + \frac{{{x^5}}}{{5!}}...[/math] So summation of algebraic series brings in algebra How are we doing ?
-
Attempting to create a generalized graph of mathematics
I intend to post a diagram (it's too scruffy at the moment) later tonight. Whilst you are still online look at these links https://en.wikipedia.org/wiki/Mathematics https://en.wikipedia.org/wiki/Glossary_of_mathematics
-
Youtube says the 2nd Law is Broken.
Accepted let's move on. Clearly all those years of experience, plus more which must have been spent in study of the subject, have given you command of Applied Thermodynamics (along with other subjects). As shown below You are not the only one who has had additional thoughts as a result of our discussion. It has also made me realise something I should have realised before. Thank you for that. +1 In another recent thread here at SF, a teacher of thermodynamics asked how to introduce the subject of entropy, without using the traditional second law approach. The discussion in your thread made me realise that of course you cannot use much of the mechanism of the second law if you are going to do this. This must be why the early diefintion did not mention entropy : entropy had yet to be defined. Hindsight allows an applied thermodynamicst to use formulae and techniques out of the logical sequence of the definition. This is in fact what I was doing and led me to my original agreement that you cannot use the classical approach to prove or disprove the kinetic interpretation. You need additional material for this. Perhaps my digression to show why the early pioneers always referred to cyclic processes was excessive, but I hope you have come to realise that since the kinetic approach is non cyclic in basis, you cannot use that part of classical thermodynamics which is defined only for cyclic processes. So another way must be found. But the kinetic question in the OP is not applied thermodynamics it is more fundamental than that. So discussion must follow and hold to a formal logical sequence of definitions and results. I don't know if you have heard of the Massieu and Planck functions ? These two provide the (mathematically derivable) link between the classical and the statistical approach, so that this is often referred to as 'the Massieu Bridge'. All of this is expounded detailed in Guggenheim's Advanced thermodynamics. (I would not recommend the Wikipedia pages on this they are rather unhelpful and not completely comprehensive or correct) However, just are there are several approaches to classical thermodynamics, there are several versions of the statistical approach. Unfortunately the statistical versions do not always completely agree with the classical versions, fluctuations being one such area of divergence. Epstein, in his famous textbook, included a whole chapter on the experimental evidence for and theoretical basis of such divergence. Epstein A textbook of Thermodynamics A free pdf is available here. https://archive.org/details/textbookofthermo031032mbp/mode/2up I am not sure of free pdfs for Guggenheim.
-
Attempting to create a generalized graph of mathematics
As I think your project is very worthwhile I have been giving some serious consideration to explain my tiling comment. +1 I have been rather busy today but I will post soon on that, using these pillars of Maths Arithmetic, Algebra, Geometry and set Theory in relation to trigonometry and symmetry. Meanwhile perhaps you would like to think about this category ? Mathematical notation and symbols. This is often the Cinderalla category, but it pervades all of Mathematics.