studiot

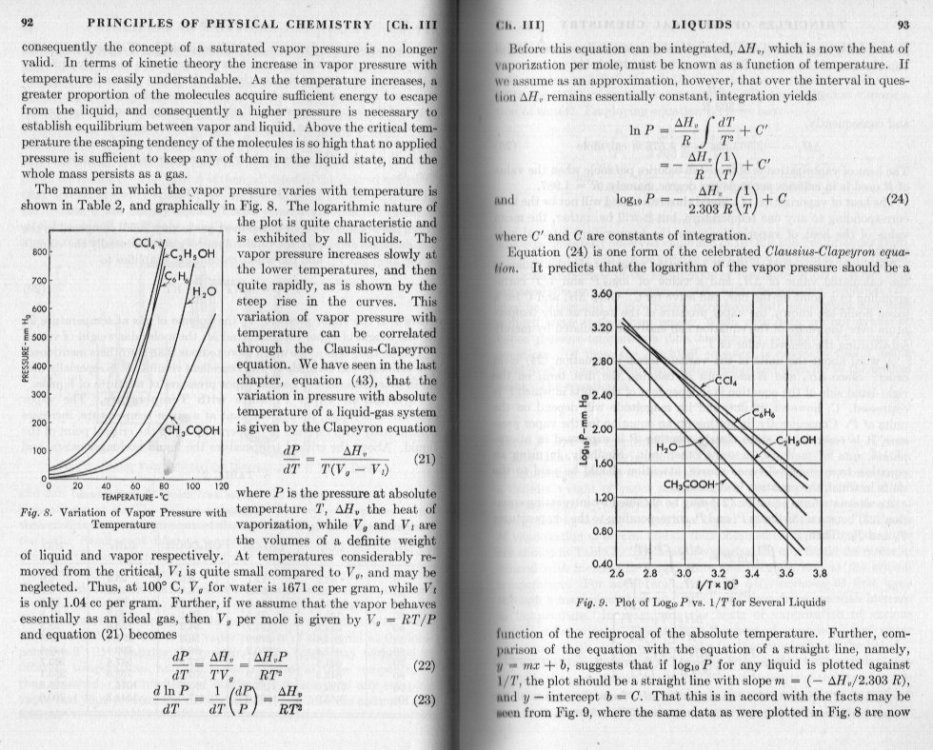
OK there are different versions of the equations and different subsequent authors apply different names. The original equations were developed for liquid- gas phase transitions, but modern trends are to generalise as far as possible and this is the version I quoted. Here is a somewhat older description, sticking to the liquid- gas model and showing how the versions are appled practically. Starting with equation 21 this is the original Clapeyron statement. Equations 24 and 27 were developed by Clausius from this.

You might find this discussion interesting and useful https://www.quora.com/Signal-Processing-What-are-the-differences-between-a-Laplace-and-Fourier-Transform

'A's are what we like. 🤓

Yes indeed the Laplace and Fourier transforms are related and very similar types of integral transform. You are effecteively asking if the 'composed time varying signal' in your diagram can be processed or decomposed into simpler signals. This is the question also answered (task accomplished) by the Fourier Transform which decomposes into simusoids. Note these simpler signals are periodic in nature. Non periodic signals may well not converge when the integral is taken. So if there periodic signals embodied in your 'composed signal' the integral proabably will not converge ie the method will not work. . The Laplace transform is actually more powerful in this respect since you can take (and untake) the Laplace tranform of allsorts of peridoc and other functions such as square waves, step functions, sawtooth waves and staircase functions. The 'formula' for the Laplace transform of a periodic function f is [math]L\left( f \right) = \frac{{\int_0^p {{e^{ - st}}} f\left( t \right)dt}}{{1 - {e^{ - ps}}}}[/math] so for the square wave shown [math]L\left( f \right) = \frac{{\int_0^2 {{e^{ - st}}} f\left( t \right)dt}}{{1 - {e^{ - 2s}}}}[/math] [math] = \frac{{\int_0^1 {{e^{ - st}}} dt}}{{1 - {e^{ - 2s}}}}[/math] [math] = \frac{{1 - {e^{ - s}}}}{{s\left( {1 - {e^{ - 2s}}} \right)}}[/math] [math] = \frac{1}{{s\left( {1 + {e^{ - s}}} \right)}}[/math] Which may be useful if your input data is digital. Does this help?

Whilst I don't see what cigarette smoke has to do with the OP, the rising smoke is an example of flow which becomes turbulent. You were quite right to observe that our best analysis of the dynamics of a turbulent system is probabilistic, though the probability is much more complicated and much less understood than Boltzman.

Inappropriately altering the ocean currents is one of the greatest dangers we face. There is an enormous disparity between the solar energy received in equatorial regions and that received in higher latitudes, both north and south. It is the world ocean circulation currents (now known as the conveyor) which distribute some of this energy to higher latitudes permitting the temperate zones to exist.

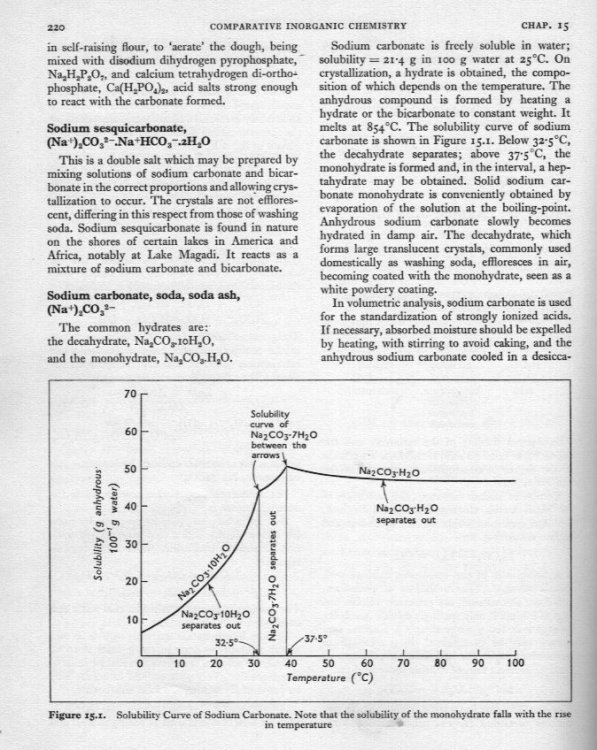
Soap is an artificial compound called sodium stearate. Soap nuts are the fruits of the soap nut tree which contain a substance that looks a bit like liquid hand soap but is 100% natural and called saponin. Saponin is a natural detergent (detergents are a general term for cleaning compounds that work with water). I thought we had answered that rather fully. Sodium carbonate has several different crystalline forms, which are rather temperature and moisture dependent. The temperature of This is exactly what my diagram shows. Below 30oC, the decahydrate is the stable form and its solubility drops rapidly with temperature, hence your crystals. Because solution of the decahydrate required intake of heat, dissolving lowers the solution temperature further promoting crystallisation. Warming these a bit drives off some of the water of crystallisation and the crystals revert to another form, the heptahydrate as the whitish powder coating on the outer parts since that is where the water leaves the crystals. You will not get the anhydride unless you heat very hard and your starting point (the bicarbonate) will probably reduce to a mixture of carbonate and bicarbonate when you first put it in the oven. This is called sodium sesquicarbonate.

Do you know what a halide is? If not, that is a good place to start.

Kinda depends where you are. There is a definite shortage of Chemistry tutors in my region (SW England) and those there are charging silly money as a result. I was talking about this last night to a friend in Oxford who place science tutors and he said there is no shortage in Oxford and no price premium there. A word about exams. It is difficult to achieve high marks in the essay type questions, and it takes longer to answer a question as compared to the calculation questions. So get your brother lots of (calculation) practice questions - there are plenty of books of these available including cheap second hand ones. On aspect of doing calculations is that you need to know the theory (which you say he does) to attempt them properly, so doing calculations make one look up missing points of theory. Also get him to join up here at SF and post questions. We have several high school chemistry students who find good quality help here.

I had no knowledge of the newer american method. One can learn something every day. Thanks for that.

I don't quite see how ? The Wiki article I linked to says quite clearly that the bicarbonate is manufactured first as a precursor of the carbonate. Since sodium carbonate is quite soluble, but calcium carbonate is not, you are not likely to find much sodium carbonate free in Nature. So it has to be prepared from a soium salt (commonly the chloride). The original process (LeBlanc) was by way of sulphuric acid, the modern(?) process (Fresnel-Solway) is via ammonia. There is also an alectrolytic process, based on the Nelson Cell which makes it directly from carbon dioxide and sodium hydroxide. But then you have to get the hydroxide from somewhere. Here is some more (numeric) information which confirms why you are having to heat your decahydrate crystals. Heats of solution are as follows Anhydrous salt Na2CO3 + Aq = Na2CO3 (aq) ΔH = -5640 calories Monohydrate Na2CO3.H2O + Aq = Na2CO3 (aq) ΔH = -2250 calories Decahydrate Na2CO3.10H2O + Aq = Na2CO3 (aq) ΔH = +16160 calories The negative sign of the first two indicate that heat is evolved on solution of the salt, making the reaction thermodynamically favourable. But the decahydrate absorbs heat (positive sign) to dissolve, which is why you have to heat it.

In the Solvay process it is the other way round https://www.google.co.uk/search?source=hp&ei=FBIPXsSDO42SlwTIpaP4CA&q=solvay+process&oq=solvay&gs_l=psy-ab.1.5.0l10.36.1856..4066...0.0..0.122.512.4j2......0....1..gws-wiz.......0i131j0i3j0i10.6J4n6xsJMwk

Thanks Each bracket is one term in the finite sequence and contains four numbers, which change from bracket to bracket. The sequence has a modulus and cycles every n terms around this modulus (in this case 32) {1, 32; 2, 31}, {3, ?; 4, ?}, {?, ?; ?, ?} , ... Hint 2 : Johannes was an old fashioned bookbinder.

Have you tried soap nuts? These are a totally natural products from the soap nut tree and are used instead of detergent in some countries. I can testify that they are inexpensive and do work well in a washing machine. https://www.google.co.uk/search?source=hp&ei=uQoPXvCAKpTQgweelJGYBw&q=Soap+Nuts&oq=Soap+Nuts&gs_l=psy-ab.3..0l10.1224.3892..5280...0.0..1.1226.5746.3-1j2j2j1j2......0....1..gws-wiz.......0i131j0i10.GH4AF607l_o&ved=0ahUKEwiwwZ-rkOfmAhUU6OAKHR5KBHMQ4dUDCAc&uact=5

Indeed +1

Hint {1, 32; 2, 31}, {?, ?; ?, ?}, {?, ?; ?, ?} , ...

This page might interest you. Note hte abrupt solubility change in the temperature region you mention.

Surely it would be cheaper to buy ordinary wahing powder/liquid/balls than to run you oven for an hour?

Do you know there is a heirarchy of 'group' definitions? They all start with a set and binary operation, but do not necessarily obey all 4 group axioms. Groupoid is the most general and is just that a set with a closed binary operation, but not necessarily associative. (axiom 1) For example the set of positive real numbers plus the binary operation a + b = √(a2 + b) is a groupoid. Semi-group or Hemi-group and is just that a set with a closed binary operation, but also associative. (axioms 1 & 2) Monoid is a semigroup with an identity element. (axioms 1 & 2 & 3) A Group is a monoid in which every element also has an inverse. (axioms 1 & 2 & 3 & 4) And thank you for taking me down a path I don't usually frequent as an applied mathematician, although all these definitions have a place in numerical analysis. +1

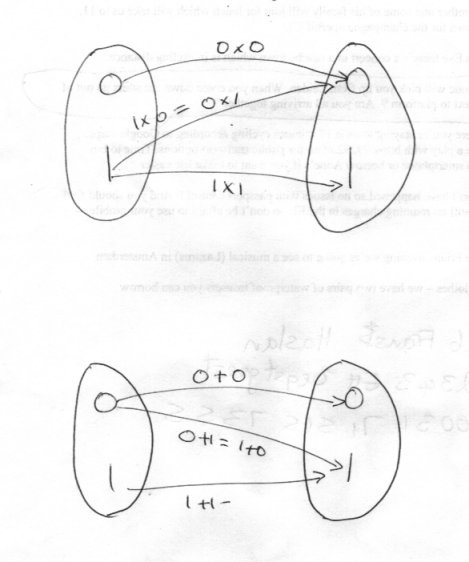
Not sure how {1, 0} forms a group under either addition or multiplication, since both have an element with no inverse.

Hello, I was away for Christmas so did not see your question. Your English appears good and I wish I could say it will be fine, but looking at your question paper learning enough to pass that in 6 months is a very tall order. The (English) Open University has an introductory self test for those wanting to take technical courses. http://mathschoices.open.ac.uk/are-you-ready-quizzes Try it and let us know how you get on. Another good resource if you can get to a library is the introductory chapter in most engineering mathematics texts. This usually covers enough maths to get you going in the book. Also have a look at this book (cheaply available second hand) https://www.amazon.co.uk/Mathematics-Recovered-Natural-Medical-Sciences/dp/0412410400

Thanks I should have realised the set you meant. The point is that the definition of a group requires that whatever you take as the single binary operation must have an inverse for every operation. This disallows multiplication, since multiplication by zero does not have an inverse. It does work if your binary operation is addition however. (and yes it also requires one element is the identity element, which also works with zero as the identity element)

Can you clarify your notation here please ? Is the interval specified open or closed? Further, if you are specifying that interval and the binary operation as multiplication then surely 0.5 is in the set but the inverse of multiplication by 0.5 is multiplication by 2 which is not in interval? As regards (im)predicative definitions Russell specified that all definitions should be predicative in his type theory for this reason. You might also like to look up Grelling's paradox of semantic self reference or heterological paradox.

In the low speed situations you describe Newton always applies. If course it depends exactly what you mean Mechanical Advantage = Load / Effort and an ME of greater than 1 is certainly achievable with suitable arrangements. Of course you need to go a long way further back than Newton for some of these, right back to the ancient Greeks. "Give me a long enough lever and a fulcrum and I will lift the world." https://en.wikipedia.org/wiki/Mechanical_advantage

Complete the sequence {1, 32; 2, 31} {....}...{....}.... Any suggestions as to what it represents?