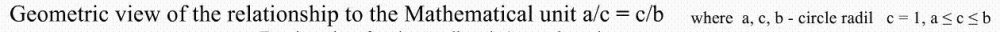studiot

Computing science has its own alternative dfinitions for many things including vector. I hadn't heard the one about a scalar but the indivisibility part makes sense since it precludes complex numbers, quaternions etc, which can be dissiciated into real and imaginary parts. However my only Discrete Maths text to define scalar say that it is simply a real number (which of course has a special meaning in computing) . Concrete or Discrete Mathematics is the correct topic home for this issue. @bufofrog On the matter of scalar - vector -tensor classification a tensor can be said to have a magnitude and two (or more) directions. But a tensor is also a vector as defined in a Linear Analysis vector space.

Thank you for your answer. Note that all semi linear and quasi linear equations are actually non linear but they can often be reduced to a set of coupled or simultaneous linear ones. You first equation is non linear because u is the dependent variable x, t are the independent variables so we only look at u and its derivatives. The first term is linear because the first derivative (of u) is not multiplied by another function of u or its derivatives. The second term is linear because the second derivative (of u) is not multiplied by another function of u or its derivatives. But the third term is non linear because it contains u2 . Have you identified the dependent and independent variables in the other equations and the non linear parts ?

Well I am still waiting for some actual mathematics from you, as well as a response to my question. I have posted circuits and mathematics to which you also have not responded. What do Fourier series the Telegraph equations (or their parent transmission line equations) have to do with Maxwell's Mesh Theorem? You cannot use the mesh currents in either FS or transmission equations as they are virtual currents. [aside for those who may be interested in the special nature of this method] Virtuality is their special nature, they are not the actual currents. Maxwell was a polymath in that he wrote extensive treatises in several areas, Mechanics, Thermodynamics as well as Electromagnetism. As such he was familiar with the 'virtual work or virtual displacement method' in Mechanics. The virtual displacement method pairs a set of real or actual forces with a set of imagined or virtual displacements in place of the actual displacements. This is done for ease of calculation and is permissible under the principle of superposition. This leads to solution of the forces, which in turn leads to solution of the actual displacements. The Maxwell Mesh Method is the electrical equivalent of this, pairing actual voltages with virtual currents, leading to solution of the actual voltages, in turn leading to solution of the actual currents. [/aside]

This is completely true. But it does not answer my question. to explain quasi linear and semi linear we need to write out some example equations. So which notation is your book using for the PDE ?

The earliest and still classic experiment involving the relativity of time (and space) is the lifetime of cosmic muons v laboratory ones. Here is a direct comaprison where Newton breaks down and Einstein takes over. http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/muon.html

Thank you for your reply to my comments. I understand that your thought processes run along different paths than those of most scientists so their output presents differently. There is nothing wrong with this, indeed it can sometimes be productive. You have certainly been polite and acknowledged the points of others so I am going to add +1 to cancel the downvote I can't see any justification for. Some things you need to know about Geometry are: Geometry can use, but does not require, measurement or scaling. Scaling is an additional property of images due to specific physical circumstances. ~~So for instance every equilateral triangle is similar to every other one, regardless of size. But there is only one equilateral triangle with any particular size. Any other equilateral triangle of the same size is just a copy of the first one. We call this congruence. Thus we can separate the properties of shape (eg equilateral triangles) and scale or size. This has consequences. In the 1960s size independent shapes were discovered when fractals began to be developed. Fractals have the property of being the same shape at any scaling. Mathematicians are happy to have just numbers on graph plots, or even no numbers at all. But graphical presentation of data can easily be distorted by inappropriate scaling. I'm sorry I used to have a book with lots of good examples, but I can't find it at the moment. So you have to be careful when presenting data. If that presented data represents something physical, with its own physical units then a further factor comes into play. People often get confused when the physical quantities represented on a graphical plot are different for different axes or coordinates. This is especially true of Scientific dataplots. And Science makes a lot of use of these plots.

Hi, Liz, What does your textbook say ? I ask this because there are several different ways to approach this and I don't want to confuse you with a different one than you are used to. does your textbook use x2Uxx - yUxy = U Which is linear and x2Uxx - yUxy = U2 Which is non linear or the same two equations written like this [math]{x^2}\frac{{{\partial ^2}U}}{{\partial {x^2}}} - y\frac{{{\partial ^2}U}}{{\partial x\partial y}} = U[/math] and [math]{x^2}\frac{{{\partial ^2}U}}{{\partial {x^2}}} - y\frac{{{\partial ^2}U}}{{\partial x\partial y}} = {U^2}[/math] Or possibly even like this. This is known as operator notation. Note these are different eqautions from before. [math]L\left[ U \right] = \left[ {\frac{{{\partial ^2}U}}{{\partial {x^2}}} - {c^2}\frac{{{\partial ^2}U}}{{\partial u\partial y}}} \right][/math] which is linear and [math]L\left[ U \right] = \left[ {{{\left( {\frac{{\partial U}}{{\partial x}}} \right)}^2} - {c^2}{{\left( {\frac{{\partial U}}{{\partial y}}} \right)}^2}} \right][/math] Which is non linear It is important to be able to separate PDEs into linear and non linear as a first step.

Newton and his contemporaries described the world in terms of 'forces'. Neither Newton, (nor Hooke) knew about the fourth great natural force - the electromagnetic force. In fact they only knew of two of the four of what we now call the four fundamental forces of nature. They also built upon the newly invented (by Descartes) maths of coordinate geometry. It should be understood that the maths and physics go hand in hand so force methods are suited to cartesian geometry and this type of geometry conditions physics thinking. Most people have an intuitive idea of a force as a driver which causes something to happen or change. They are also familiar with the idea of one force resisting another, leading to the notion of a balance of forces. The two forces (mechanical and gravity) coupled with the opposition / balance notion are enough to generate a whole wide range of physical phenoma from structural theory to vibrations at light frequencies (Newton did not do this ) to understanding why we do not fly off the spinning planet to ballistic theory enabling warships to aim for and hit targets they cannot see over the horizon and just so much more. So when asked "Why do the planets orbit as they do?" Newton's theories answered in terms of forces and the balance between mechanical (inertial) forces and gravitational ones. The next step was not relativity but energy methods that were developed one to two centuries after Newton. Here the idea was to consider the energy involved when a force acts or is opposed or balanced. A new notion of 'least energy' was introduced and names such as Castigliano, Maxwell, Hamilton and Lagrange came onto the Scene. A devotee and substantial developer of Newtonian thinking was Euler. Right at the end of the time a new type of geometry appeared, developed by Riemann. This new gometry was just as well because it allowed the flaws in the Newtonian system that had become apparent in two centuries of development, to be addressed. Thus was ushered in the new system of Relativity, which is really a change of Geometry, not Physics., although derived from physical considerations by Einstein. It was substantially fleshed out mathematically by maths professors Minkowski and Weyl. Along with the discovery of the electromagnetic force and two nuclear forces replacing Newton's collection of mechanical forces, the energy methods went on to blossom into the quantum theory. This is a very short form history of 500 years or so of development into modern Science.

Like you other thread this one provides a good learning opportunity in focusing your questions (both are good questions whne focused) Swamps are wetlands so can be salt water (like tropical mangrove around south sea volcanic islands) or freshwater (like in northern Russia. ) (Both have swampland plus volcanoes) These make a difference and you need to distinguish the sources of water. Fresh water will need to come from higher land with perhaps extinct igneous activity. You say both dormant and active volcanoes. Sometimes the rocks provide the source of solid/soil material, which determines the nature of a swamp. Sometimes the solid material comes from decaying living matter to form materials such as peat. So tell us more of your interest to focus this thread.

Hello COM, and welcome. ScienceForums is a good place to com ask questions and learn new stuff. I notice you have asked a second question since this one, but not tarried in this thread. Other members who put in effort to help you appreciate your further input to what is, after all, your subject. Anyway the word you ned to search with is 'caustic'. (Google etc) Caustic is a general technical term for substances that can chemically attack tissue, both living and dead. It somewhere blends into 'corrosive' . Corrosive substance attack tough inert things like metals and rocks etc. As has already be said, many caustic substances rely on being acid or alkaline; however I note you are particularly interested in 'natural' substances so here is a good resource Atkin's Molecules Peter Atkins Cambridge University Press. Peter describes lots of molecules importart to us including those that can have a burnsing effect in sufficint concentratin for example the substances in pepper and chilles Piperine and Capsaicin.

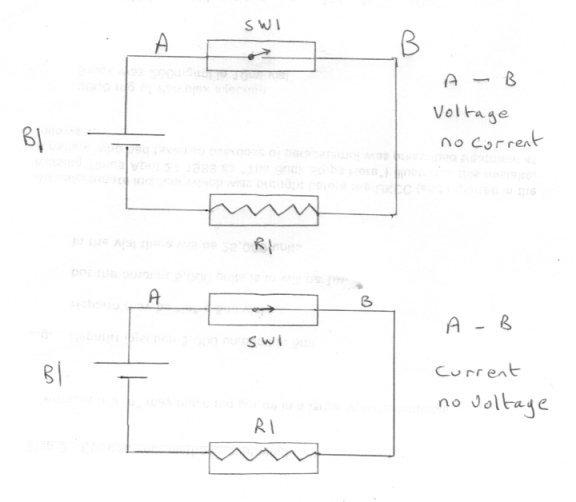
In case my last example was too difficult here is a simpler one. I have formed two different circuits, using the same three circuit elements. In the first circuit switch SW1 has the entire circuit voltage across it but carries zero current. In the second circuit the same switch has zero voltage across it but carries the entire circuit currrent.

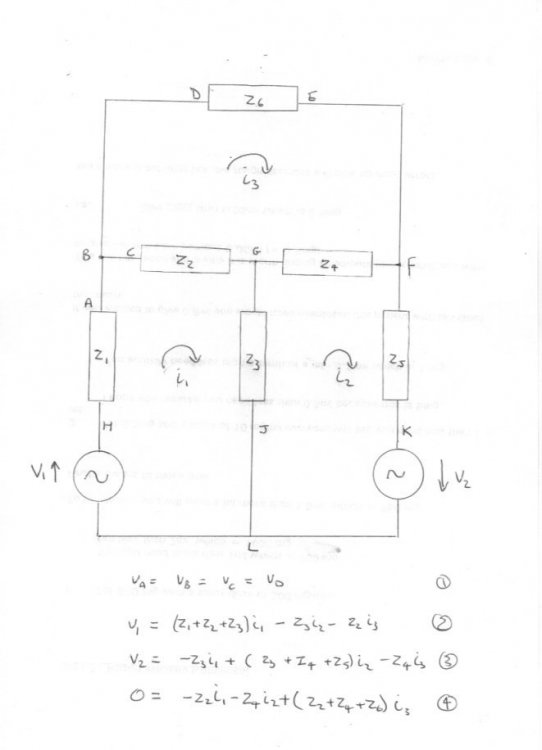
Well I had a great Christmas in the home of both the DC electric battery and Superconducitivity. I see you have responded to others but not to my serious question about circuit theory. So let us stop beating about the bush, here is a small mesh which demonstrates the falsity fo both of your claims. For generality I have written complex impedences and AC generators, but the results are equally applicabl to DC meshes. I see Sensei has already dealt (mathematically) with some of your incorrct claims about DC electric circuits +1 So I have written The basic definition condition of the connecting wires for any network as my equation 1. This clearly asserts that The voltage at any point on a connecting wire in Circuit Theory is identical to the voltage at any other point on that same connecting wire. So that has dismissed your claim once and for all. Secondly note my equation 4 equally asserts that the mesh currrent in loop BDEFB is circulating with zero loop EMF Thus you have current but no voltage around the loop (although yhere are voltage differences bewteen certain points partway around the loop). This need not involve supeconductivity or any esoteric stuff, it is achieved with any old common or garden circuit elements. I am sure you ar familiar with the battery? So there you have voltage with no current, if the battery is not connected to anything. So let us have no more nonsense about Voltage with no current and current with no voltage.

Although it may be bureaucratically desirable to masure the size of everything via a ratio to a standard, it seems to me thare are severeral (mathematical) problems associated with this approach. 1) Surely you don't mean the mathematical unit but the algebraic unit, for is not Geometry also part of mathematics ? 2) In terms of algebraic difficulties what happens when a = b = c = 0 ; in total accord with your stated algebraic conditions ? 3) In terms of you geometric version, how do you compare the sizes of two spheres? By radius? by surface area ? by volume ? Each will yield a different numeric answer.

Whilst I am away, have a happy Christmas reading all the parts of my posts you either didn't or ignored. In particular I mentioned Maxwells's mesh theorem, since you like Maxwell. Are you aware of th special nature of the current in that theorem?

But this is just not so. Whilst a static discharge is certainly between two places, it may or may not be between two charges. Unless you can convince us that the enormous charge in a thudercloud that sends a lightning bolt down to strike an electrically neutral tree is somehow between two charges. Or perhaps the smaller charge carried by a person and discharged to an electrically neutral door knob is also between charges.

Although not completely correct in your conclusions, you seem to have stumbled on an important aspect of the difference between space and time and this is a good way to describe it. The point abut the length of the tree comapred to the length of the metre rul you mentioned earlier is embodied in some theory known as the Relativity of Simultaneity. https://www.google.co.uk/search?source=hp&ei=i6T_Xc-XMY-qUMTZkYgH&q=Relativity+of+Simultaneity.&oq=Relativity+of+Simultaneity.&gs_l=psy-ab.3..0i22i30l10.648.648..1674...0.0..0.186.186.0j1......0....2j1..gws-wiz.GXAhxkIHwvs&ved=0ahUKEwiPiZnk4MnmAhUPFRQKHcRsBHEQ4dUDCAc&uact=5 When comparing an object. either to a measuring stick standard or directly to a coordinate framework itself, to measure its 'length' you have to have this concept so that you compare both ends of the object measured at the 'same time'. I know of no corresponding requirement to compare the readings on two clocks in the 'same space', although you may have to adjust (transform) the framework to a common base. So +1 for encouragement.

Thanks fot that +1 Interestingly We are visiting Leiden for Christmas. More interestingly I learned this on ScienceForums a year or so back when I thought (as you did) that superconductivity was just very low resistance and someone corrected me. Whn I studied this stuff suprconductivity was known but far from well investigated or mainstream. Now of course it is largely understood and has practical uses.

What can one say to an electrical engineer who denies Kirchoff's voltage law Kirchoff's current law Rosen's Theorem Millman's Theorem Node analysis Loop analysis Maxwell's mesh curent theorem Norton's theorem Thevenin's theorem to name but a few theorems in Circuit Theory that all depend upon defining the impedence of interconnecting wires between circuit elements as zero? Some of these can be adapted to take into account wiring impedence, but som depend upon replacing the wiring with equivalent circuit configurations embodying a different wiring and even different circuit elements. +1 to strange, Ghideon and Carrock for offering further inconsistencies. A final comment about current and voltage. Current can be driven by other mechanisms than voltage e.g. themal drift current, ionic concentration current, solar wind current, nuclear decay current.....

Thank you for that. Lost amongst the split this post of mine is directed @FlamingoMan original problem. Do I understand that this is a theoretical exercise, not a practical one from these answers? I ask because appropriate action depends upon where the person being shocked. 1) where the person acquires the charge 2) Where that person is being shocked by the discharge As you pointed out it is very common for (some) people to aquire a charge through friction rubbing against clothing, carpets etc. So I am assuming that this friction is when the person is running on the treadmill. Subsequently the person either grabs a metal bar on the running machine and is shocked. Or walks off, carrying the charge with him, and is subsequently shocked when he touches something metal, say the locker cabinet. Earthing the bar on the running machine will not help with either of these situations, nor will sweeping up the opposite charge from the moving running platform. Indeed the exposed metalwork may already be earthed. In these circumstance the discharge has to take place somehow and so the action required is to limit the discharge current to a level where it is not noticeable. Too slow the discharge down (thus limiting the current) you can interpose a partly conductive material (eg a wet towel) or if the discahrge is to a metal bar on the machine then wrap a permanent conductive foam layer round part of the bar for grabbing onto before touching the bare metal.

Yes but you should remove these bits from your answer ( in two places)

There is a force on any elbow carrying a flowing fluid due to the destruction of momentum in the forward direction and creation of momentum in the perpendicular one. Momentum therefore does not balance without the force.

Yeah that the best way.

They are the ones listed in your text book page you posted.

I put units ? for you to put in the correct units. !!!!!! 5g/10 when did you ever put units as well as the numbers into the formula for calculation ? density = 5 /10 = ? and I did ask you what the units for density are. Hint they are something per something else.

Here is what I would say. Size order smallest to largest A Neon atomic radius 71 picometres D Nitrogen atomic radius 75 picometres B Beryllium atomic radius 112 picometres C Sodium atomic radius 186 picomatres