studiot

Here is the theory you require. Make sure you get you friction force acting in the correct direction (your dashed one in this case) Also the normal reaction (again dashed) is the force ating on the wheel. The other mg at P acts on the ground, not the wheel. The moment provided by the contact point P about the centre = tangential force due to friction x wheel radius. Note the frictional force is only equal to μmg when the wheel is on the point of slipping. At other times it is less than this. All this is detailed in the text.

No it is saying that if you take the results of an experimental measurement as one of your axoims you can reduce the number of theoretical axioms. The idea of theoretical Physics is that it tries to answer the question, "Whys did we obtain that particular measurement and not a different one ?" Theoretical Physics may have some of its inquiries promted by the results of experiment, but it also like to use experiment to confirm predictions. You can't use an experiment both as an axiom and as a confirmation. This is much the same comment I am making in the current trhead on SR.

No, you can live in a quite comfortable way with a single frame, and apply, instead, Lorentz transformations to particular solutions. This gives you different, Doppler-shifted solutions. There was a simple explanation proposed by Lorentz. Namely, if what holds together condensed matter is the EM force, then condensed matter has to have the same symmetry properties as the EM equations. Thus, a Lorentz-transformed (Doppler-shifted) solution for some piece of condensed matter will be a solution too. But the Lorentz-transformed piece of matter is contracted. The actual explanation works in the same way, we have a lot more fields in the SM, but they all are wave equations with the same c, so that a Lorentz-transformed solution will be a solution too. Why do you say no ? Although your English is very good, perhaps you didn't catch my meaning. Yes it is true that if you are only working in one frame you can apply the Fitzgerald contraction to bodies in motion relative to that frame. (Note You cannot apply the Lorenz transformation, since by definition, that transforms values measured in one frame to those measured in a different frame.) But all you are then doing is finding a formula that curve fits experimental results. There is no way, that I am aware of, of deriving that formula from fundamental theoretical principles, in a single frame. However I am quite open to someone who knows more showing me how.

Hi Mordred, My comment was specifically about Minkowski's original 4D World, where he used tau to distinguish as I posted way back on the previous page. until the introduction of 'proper time' this was the use of tau. Which I grant you is confusing, especially as in the original paper Einstein used tau as time in the second frame. Minkowski has always been acknowledged as an alternative simpler route to obtain the same end result.

He said, very specifically that humans are the only species with an opposable thumb. He was just plain wrong, and googling it suprises me just how many other species there are that actually have one, in addition to those species that have an alternative anatomical arrangement that serves the same function. He also used this and also the our enhanced reasoning ability compared to other animals in the same way as the Church has done in the past - To promote the idea that we are somehow better and more deserving than other animals. This is also misguided. Anyway I also said he had some good ideas, so why are you not making a fuss about these? I try to be objective and even handed, but nobody is perfect.

Well the loss is entirely yours. I would like you to thank you for introducing the subject since several other members have found something of interest to discuss in it. So we have all gained from it, as you could have done. No I meant substitute a new variable tau. It is conventional to introduce the new variable tau to distinguish it from time. tau has the units of length as do the three spatial coordinates. This is the necessary and sufficient for treating them all equally. It is necessary to introduce 'i' to make the coefficient of the square negative. τ = ict Does this help ?

Sorry I don't know the book, perhaps Mordred ? One thing though. I would counsel caution using the explanation in any book written for another purpose. Not that it will necessarily be wrong but it will be tailored to the main application of that book and may well be incomplete as a result. We currently have a thread about boiling soup (water) due to someone applying (perfectly good) theory from somewhere else way outside the boundaries of its applicability with comic results.

In fairness to the OP he has hit upon a question to so often trips folks up. The 'system' doesn't have a temperature unless that is the same at every point in the system. So most of the equations in thermodynamics do not apply to systems to which you cannot assign a temperature. In such cases you need to break the system down into smaller subsystems (as many as necessary) to apply thermodynamics. Just sometimes you can obtain an average temperature and use this as 'the temperature of the system', but you have to be very careful when and how you do this.

Perhaps Mordred has been reading this book. This 1962 book is the only one I have ever seen that follows Mordred's route and also explains the difference between a component and a resolute (what you get when resolving a vector), and its importance. Most applied tensors are cartesian tensors, which are othogonal. In this case there is no difference but in the case of skew axes (non orthognal) the difference is vitally important. The book covers Maxwell rather well. It is also interesting to note how far mathematical expectations have come since 1962 I have included the target audience on the left. Other good easy expositions in applied science are Cartesian Tensors in Engineering Science by Jaeger Cartesian tensors by Harold Jeffreys and a bit more advanced Cartesian Tensors an introduction by Temple

Why are you so stubbornly misapplying the theory? Adding salt to the water increases the boiling temperature. Putting the lid on increases the boiling temperature and reduces the evaporation rate. Keep it simple

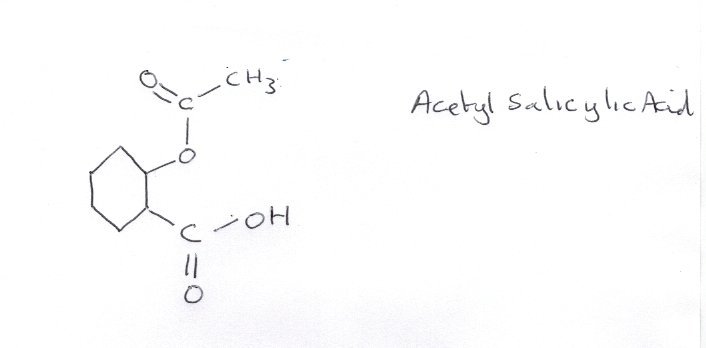
Thank you strange for resetting the question properly. I would be very grateful if you could explain to Olive how to put th question in without overrunning the page. So how many carboxylic acid groups can you identify on acetylsalicylic acid? In other words is this a monoprotic or a diprotic acid? Can you now continue?

No it does not make sense and you introduced soup at the start of this discussion. It does not make sense because you are making the classic mistake of applying a theory designed for one situation to an entirely inappriopriate one. Rather than going abroad to find fancy elaborations on what is a simple subject, why not look to your own University of Cambridge? Here is the griff prepared, taught and examined in UK schools on the subject. https://isaacphysics.org/concepts/cc_cooling_curves You need to look at the second part of this webpage where the question is applied to mixtures. Note the bowl of soup you heated is not as large as an ocean but is the sort of situation discussed in the theory you are trying to apply. Further it should not be compared with an ocean but with a similar sized bowl of pure water, where you will find that the water remains at freezing point until all the ice has melted. This experiment used to be conducted in school science lessons because there is a great deal more that can be learned from it.

Even the Archbishop of Canterbury is over 70% water. Do you expect him to melt in the same way as a large mug of ice? Let us examine your conditions more carefully. 1) Your soup will not melt/freeze at 0 degrees C because of a phenomenon known as depression of freezing point. This is due to both material (salts) dissolved in it and particles of food suspended in it. 2) Lumps of vegetable will act quite differently providing a thermal reservoir either of cold or heat with local effects in the mixture, no matter how well you stir. 3) Particles of suspended food will considerably affect the heat transfer through the mug of soup. This is why you should thaw slowly. The different constituents thaw at different rates. anyone who has frozen and then thawed a bottle of milk to quickly will have experienced this differential thawing of the components of the milk. So John and swansont are quite right to point out the lack of equilibrium and stirring (although you can't sit until nearly thawed). And the more inhomogeneous the soup, the more slowly you need to thaw and heat. As a matter of interest we thawed out and then heated some chunky chicken and vegetable soup, in the microwave, tonight. This behaved exactly as described, and we have to run the microwave at half power to get a satisfactory thaw and reheat.

I don't see any soup in your idealisation diagram. Water is not soup (at least not in Somerset) The stipulations you refer to only apply to a single pure substance. Mixtures will act differently.

This is your problem. Please show an example of your intended calculations.

As the Man said, up to 44 of them. Thanks for saving me a deal of wristache. +1 But please note that 'the metric' need not be a tensor its definition is much wider than that. An acceptable metric on the real numbers is the modulus function of the difference between any two.

What accumulations are you thinking of? Here are some basic biological facts (from Apps, Cohen and Steel University of Edinburgh) I wanted to introduce you to the vital importance of calcium in a normally functioning body. The antacids mentioned by John Cuthber, the deficiencies mentioned above and any such 'accumulations' would be an abnormal function. Calcium is not only vital for the skeleton but also in neurotransmitters and muscle action.

Good questions, why shouldn't students ask questions? +1 Another point about Pais was that Wikipedia says he was uniquely placed to write these histories as he knew many if not most of the important player. That remark shows just how polarised societies were back then. He knew none of the English speaking world at that time here is a comment from Ferreira that also mentions the imfamous "superfluous erudition" but he goes on to show how Hilbert re-educated Einstein (circled at the end) The extract also shows Eddington's position and contribution. I think I should have made clear that ds2 is the Minkowski invariant.

Well I'm sorry that your statement was so vague I misinterpreted it. I look forward to your exposition of the entry into and transport around the body of calcium for the benefit of the OP. No doubt it will be considerbly more detailed than my broad brush treatment.

Yes I agree further discussion would take us too far off topic, but by all means if you want to continue into a new thread then go ahead.

Doubtless a good book, and widely available in English. As regards the tensor research I would counsel geordie not to go there. Particularly as that would invoke the einstein summation convention. which is difficult to follow. There is no gain to be had from the use of tensors in Special Relativity. In General Relativity their use tends to obscure the Physics. However I am with the great man himself when he wrote this book This slim volume in my view "weighs an ounce, but contains a pound of wisdom" In it Einstein explains, largely in words, the thinking and reasons behind his development and presentation of both SR and GR. Originally written in 1916 I show the 15th (1952) edition in the attachment. I don't think he mentions the word tensor once in the book although he does reproduce the GR tensor metric [math]d{s^2} = {g_{ik}}d{x_i}d{x_k}[/math] and then points out that this seemingly innocous equation actually represets 44 equations in compact form. But his development of the subject in an appendix called relativity of and the problem of space in words is the clearest I have seen.

Curious use of the word humble, in this context,since it's only religion that teaches humility and strangly not off topic. The mundane expination for the start of the major religions is: a person had a good idea that could explain how another person could be content with his/her life; no need to evoke a deity or aliens. Thank you for your response. I think other non religous philosophies also advocate humility, as did and do many scientists and other thinkers. Note I said boosted religous claims. Perhaps this was too brief to convey my full meaning. I was referring to the power grab over society that characterises so many religions, although there may have been a 'good and humble' idea at the beginning. The usual development is that following the power grab the religous doctrine becomes that of the new leaders rather than that of the originator and oftetimes inflexible to boot.

Thank you for the query I will expand the explanation, but first an apology to all. I realised last night that a silly error crept into my first formula which should read [math]{d_{AB}} = \sqrt {\sum\limits_0^{\left( {n - 1} \right)} {{{\left( {x_B^n - x_A^n} \right)}^2}} } [/math] This is because for some reason the pundits chose to start counting axes and dimensions from zero not 1 so the sum should be from zero to (n-1) not to n. So for 4 dimensions (Minkowski) we have x0, x1, x2 and x3 As to your second point, if some of the 'x's had a minus sign, how would you knowwithout writing out the formula in full? For the space to be Euclidian, every axis has to have equal value or weight ie the same physical dimension. A Euclidian space is a geometric space and you can't do geometry in a space where some axes measure length, some say time and some say something else eg temperature. So it is perfectly acceptable to use x0, x1, x2 and x3 or x,y,z,ct or x,y,z,ict since all these spaces have the same underlying geometry, provided you write out the metric formula correctlyin full. To do this you would need either the first or last to also use the general formula. But it would not be correct to call x,y,z,t Euclidian. The advantage of the general formula is that you can explore the effect different numbers of spatial and time dimensions. Eddington considers this You can also do something further. Since when using x0, x1, x2 and x3 the axes are not only physically equivalent, but symbolically equivalent as well you can explore more complicated metric formulae. Eddington does this as well. The Euclidian Minkowski metric is called the 'four squares metric'. Squares imply quadratics and Eddington considers the general quadratic and the implications of reducing it to the four squares one for Relativity.

Neither. But I had just watched an interesting Natural World TV programme about Bears. One species of bear apparantly has an opposable wrist that he can manipulate in conjunction with his claws, like our thumb and fingers. He can also develop mental 'maps', remember them and use them for future planning. I did not know this until I saw the programme and the video of those bears. I do know that many species can emulate some of our capability or another, perhaps in a small way. But your author was claiming we are the only species that can........... I humbly suggest we need to beware of such puffed up self importance that once boosted religous claims.

Sure thing. A 'space' is a set of points with particular properties. If one of those properties is a 'distance function' then it is called a metric space and the distance function is called the metric. A distance function applies in an identical manner to all possible pairs of points in the set with a positive definite ( greater than zero) result - it can never be negative. (but not necessarily an identical result this distance of London from Rome is not the same as the distance of London from New York, though each mile is the same as any other mile). It is zero only in the case of the the 'distance' of a point from itself. A Euclidian space is a metric space with the Euclidian metric which is [math]{d_{AB}} = \sqrt {\sum\limits_0^n {{{\left( {x_B^n - x_A^n} \right)}^2}} } [/math] for an n dimensional Euclidian space (conventionally counting dimensions as x0, x1, x2.......etc Note here that n is not a power but an indexing label for the dimension. For Minkowski space with axes labelled x,y,z and tau this becomes [math]s = \sqrt {{{\left( {\Delta x} \right)}^2} + {{\left( {\Delta y} \right)}^2} + {{\left( {\Delta z} \right)}^2} + {{\left( {\Delta \tau } \right)}^2}} [/math] Which is the formula for the invariant spacetime interval s. So 's' is the Euclian metric on spacetime from which we derive Lorenz. A student of General Relativity would say that GR reduces to flat (= Euclidian) geometry when we consider local (infinitesimal) effects and SR is 'flat' spacetime. This is good because GR is amenable to differential geometry because this is true.