studiot

Although the subject matter is touchy for some, this is a very good way to introduce your question. +1 I haven't yet looked at the PDFs, but the title and claim that "the Coulomb field (& also gravitational fields) travel with infinite speed." is suspicious. Suspicious because coulomb and gravitation fields do not travel, unless their source is moving. In the latter case they have the same motion as their source. It is signals, disturbances or changes in a field if you will, that travel. A niggly point perhaps, but one would have hoped a real scientist would have got that right. I have just downloaded the pdfs and they look regular but old (2014 for the original) The first paper is 23 pages long and I have a vague memory of seeing it before The second is only 3 pages (thankfully). Both are innocuous. More when I have read them.

I assume you are referring to the UV emission/absorbtion spectrum of methane, by ejection of an electron ? Surely this apparently cut and dried response is falling into the all too common trap expecting an Aristotelian logic (A) or (not A) from QM. QM is not deterministic like classical mechanics. Here is a short comment from this discussion of your issue. https://chemistry.stackexchange.com/questions/32038/are-the-bonding-orbitals-in-methane-equivalent-photoelectron-spectrum Have you considered what happens when observing the IR spectrum of methane?

You are right to be somewhat skeptical of that presentation because it misrepresents what Einstein postulated. He did not postulate that the speed of light is 'the same for all observers' as the narrator suggests. (He actually proves this and something more which the narrator omitted). Here are his original two postulates. His proof of observer independence came after three pages of deductive reasoning on pages 6,7 and 8. It is thus a consequence of of the original postulate of source independence. I think he made it this way because his reasoning did not require light to be a wave phenomenon. His original second postulate could have been taken from the already known properties of waves had he 'assumed' light to be a wave phenomenon. Subsequent scholars simplified the postulates to include the observer. Einstein also realised that the 'master postulate' is the principle of relativity and thus that he also had to prove that the second postulate is compatible with the first. This he stated on page 8 and proceeded to verify.

There is somewhat a measure of fashion about what symbols are used for what purpose. In most english language texts on coordinate geometry a straight line has the equation y = mx +c. You are not entirely wrong. It's just that you were using two points. A mathematician would be perfectly happy with the answer "the slope is m." , since any value of m will suffice. Or if m has been specified (say 0.5) the the slope is 0.5. Naturally c would also need to be specified - in this case the statement goes through the point (0,0) is sufficient to identify it as equal to zero. The equation [math]m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}[/math] is just one of many derived forms, and the definitions need to encompass all of them. Here is a short list As a matter of interest I included that stuff about the field {1,0} because it is discrete and of tremendous use in truth tables and computing mathematics. Fields have many other use for instance they are part of the basc definition of a mathematical vector and vector space axioms. So abandoning them to allow division by zero would have unwanted rippled throughout applied maths.

Well I think the question is directly on topic since it directly address different models of light propagation and ties in with my spherical v plane wave comment. Like many complicated phenomena we have many models of the phenomena, partly as our knowledge has increased and partly because we only need our model to be able to provide answers to questions we are interested in. So the simplest form of optics is called 'geometrical optics' and is really the rules of 'light rays'. Next up on the list is the wave theory of light. Then we have relativistic theories. And finally quantum theories of behaviour. Each of these theories/models addresses more and more of the observed behaviour of light and must of necessity default to the simpler one in the list where they both address the same properties. So the wave theory must explain the tenets of geometrical optics 1) Light travels in straight lines 2) Rays originating from infinity are parallel It does so because it works on phase or phase difference of the light wave. If you can imagine a circular (spherical) wave emanating out from a source you should picture a series of concentric circles around the cource. Each of these circles is an isophase line - a line of constant phase or a (circular) line where the phase of the light is the same. Close to the source the curvature is large and the radius small. The radius is normal to all of these concentric circles and forms the ray. As the radius becomes very large the curvature of the circles flattens out and neighbouring lines normal to the circles become more and more nearly parallel Until at infinity they become mathematically parallel. We take the distance between the Sun and Earth as sufficient to count as condition (2) above then we can say that in wave theory the original spherical waves have become plane waves ny the timethey reach the Earth. In geometrical optics this condition strictly applies to on axis rays. However again we make the approximation that rays 'nearly parallel' to the axis are included. Rays which are substantially divergent from the axis will not be brought to the same image (eg the retina) surface.

Pity you didn't say this before Shows the wisdom to telling us your working. No it's not wrong, it's just not finished. So hold your nerve and keep going as HyperI says.

Yes this is true, have you seen any of the videos about the view of objects that are have relativistic magnitudes of relative motion? But that is off topic here, no? What did you or your 12 year old boy make of my contribution? What actually do you think a ray of light is, and how do you explain its existence?

This is fun but a small niggle here. How are these two statements consistent with each other? As a matter of interest, current approximations have the waves of light leaving points on the surface of the Sun as spherically expanding waves, but by the time they have reached Earth, we model them as plane waves. Plane waves have parallel rays, spherical waves do not.

I was going to start by asking Conjurer why he revived this old thread ? However there still seems to be interest in it so here my thoughts. That about sums up common or garden use of arithmetic. so +1 This is the first thread I have seen you post that is coherent and rational, even if it is partly flawed. However you have identified and highlighted the correct part of the OP which is that there is something different about division by zero. So +1 A small niggle, I would say that the simplest equations in a plane is the line y = k or x = h, where h and k are constants. The idea of proportionality is good but more restrictive since my two equations do not display proportionality. However we should always require general statements to cater for the most general case so I will continue with equations. Ghideon is correct here. The constant of proportionality is well constant, which means it is defined as having only one value. But as I said, employing it is restrictive. Employing the slope of a line is even more restrictive and I think both you and Ghideon are wrong to use it. Particularly as Ghideon's definition does not even include the more general case of y = mx, where the slope at a single point is defined. OK so what to do? Well we are dealing with the arithmetic of numbers and when faced with this situation Mathematicians turn to Set theory. The numbers come from a particular type of set called a Field. To qualify as a Field both the set and its elements must prossess certain properties. Importantly here the set must have at least two separate 'binary operation's defined on it. These can be defined by equations a + b = c and a * b = d where a, b, c and d are elements of the set and are commonly called addition and multiplication. Note there must be at least 2 operations, not or 1. Some fields have additional operations, but they are not used in arithmetic or required in the definition. The elements of a Field are all of the same type which means that c and d must be numbers (in our case) of the same type as a and b. There are several other requirements (to total 9 in all) collectively called the Field axioms, But the other important one to us is that no number can be missing. This is called closure and the set is a set of all numbers of the type of number we are using. This will, of course, include zero itself. So not all sets of numbers are Fields. This curious setup has many advantages which allowing division by zero would take away from us. But there is already a slight difficulty creeping in. The advantages are that this setup guarantees that every equation of the sort a + b = c and a * b = d will have a solution, with one exception. And also that whenever we perform these binary operations, we will always get a number and nothing but a number. and further we can do this for each and every pairing of numbers. The exception is that there is no solution to equations of the type 0 * a = 9. This is resolved by disallowing division by zero. The phrase division by zero is not defined. A small price to pay for the univesality and usefulness of the normal system of arithmetic. Three further notes. Firstly the smallest field is the field with just two numbers, 0 and 1. It is mathematically possible to define a mathematical structure (called an extended field) by adding special elements which will allow division by zero. But the price is that the extra elements are not numbers and we cannot guarantee what we will get if we use our equations. Finally division by zero and the fraction 0/0 are different and require different handling.

Yes HCl is officially a strong acid which means that it is fully dissociated at the concentrations to produce a pH of 2. pH is defined as the logarithm of the reciprocal hydrogen ion concentration. This also equals the negative of the log log the hydrogen ion concentration pH = -log[H+] (Some people like to use the hydroxinium ion H3O+, but I see little point for this purpose) So you need the hydrogen ion concetration, in moles per litre. Can you have a stab at it now? What is the dissociation reaction? Here is a tip if you are plotting something against pH in you experiment. pH conc of HCl to achieve that pH in M/litre 1 0.1 2 0.01 3 0.001 4 0.0001 5 0.00001 This is very easy. It is more complicated if you use a weak acid such as acetic, which often happens in biochemistry.

So let us start with the basics. Do you understand what a pH of 2 means? Do you understand the difference between a strong acid and a weak acid? Which do you think hydrochloric acid is?

Build your formulae in one of these and copy/paste into SF. https://latex.codecogs.com/ or http://www.sciweavers.org/free-online-latex-equation-editor

d(flux)/dt gives an induced voltage (with a sign) So putting this into mathematical form [math]d\Phi = - BdA[/math] divide both sides by dt [math]\frac{{d\Phi }}{{dt}} = - B\frac{{dA}}{{dt}}[/math] Where A is the area enclosed by the (triangular loop) Faraday's law. [math]E = - \frac{{d\Phi }}{{dt}}[/math] Where is is the voltage generated in a wire at right angles to the field Now draw some positions of the blue wire in at varous times. Also extend the velocity vector of the blue wire in both directions. What do you notice about the triangular areas so formed? Can you connect this to the above in terms of the velocity of the blue wire? The point of the similar triangles is that you don't need any actual values of area, ratios will do. One further note. E is generated only in the blue wire because it is the only wire moving. The black wire is stationary in the field so no voltage is generated in this one. The circulating current in the loop is entirely due to the motion of the blue wire. One final twist - is the blue the blue wire motion at right angles to the field, in accordance with Flemings rule?

https://byjus.com/maths/area-of-similar-triangles/https://byjus.com/maths/area-of-similar-triangles/ You will need both lengths and areas

I had thought this was not homework for a formal course you are doing, online or off. How are you getting on with the geometry? When you come to it how do you think the slant angle will affect Flemings generator rule ?

You obviously didn't read the book where they introduced hybridisation.

Please note the date of the OP.

So where did this question come from and why are you doing it?

My suggestion is to do the geometry first. Look up the properties of similar triangles if you don't already know them Use these properties to find out the rate of increase of the area of the triangle and the lengths of the 2 wires that make it up. Then worry about the induction.

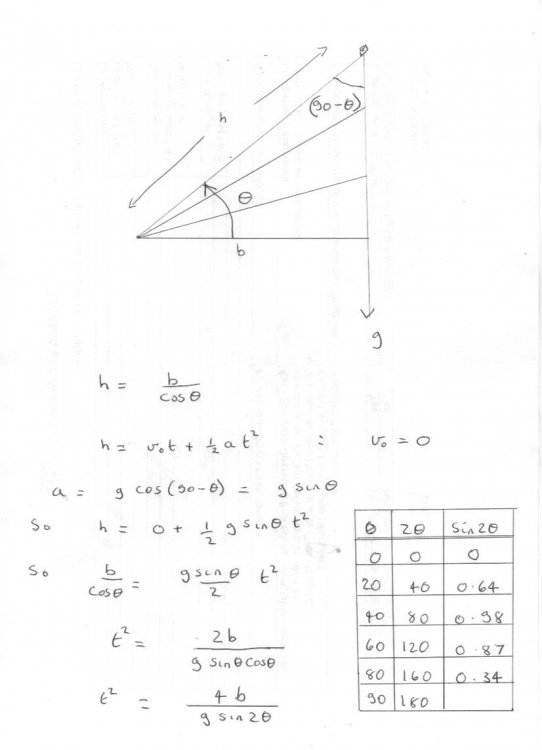
So here is one way to differentiate The rule for complicated tig expressions is "First the power, then the trig, then the angle" note this is the sine function raised to a power, not the use of sin-1 which means the inverse sine or arcsin. So taking the square root and separating the square root of the constant we have [math]t = \sqrt {\frac{{4b}}{g}} *\sqrt {\frac{1}{{\sin 2\theta }}} = \sqrt {\frac{{4b}}{g}} *{\left( {\sin 2\theta } \right)^{ - \frac{1}{2}}}[/math] using my rule above we can differentiate directly [math]\frac{{dt}}{{d\theta }} = \sqrt {\frac{{4b}}{g}} *\frac{{ - 1}}{2}*{\left( {\sin 2\theta } \right)^{ - \frac{3}{2}}}*\left( {\cos 2\theta } \right)*2[/math] Other ways involve using the reciprocals of the trig functions so 1/sin2θ = cosec2θ But we eventually end up with the same product. So looking at our derivative and setting it to zero this occurs when sin2θ = 0o or 90o or when cos2θ = 90o as the only values in range. Yes wheel out your extra ordinary problems, but one at a time please. A final question, Do you understand significant figures? We only know g to 3 s.f. So there is no point recording more than 4 sf in the calculations for the values of other quantities.

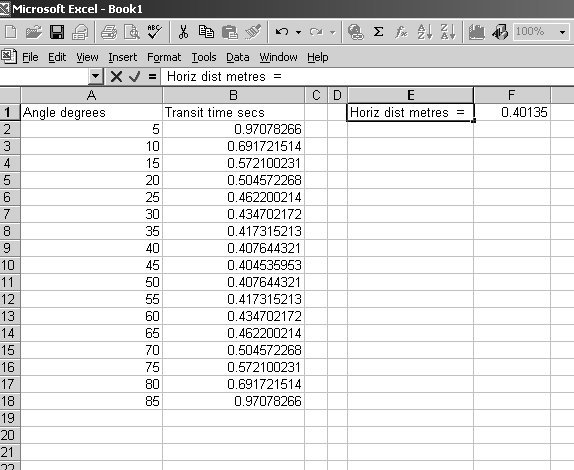
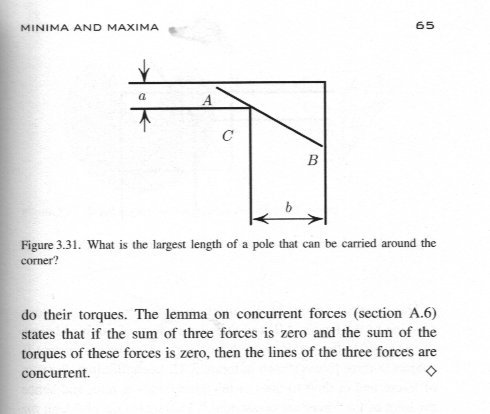
Here is an excel spreadsheet at 5o intervals Yes it gets a bit messy but not too much. Did you understand the use of the double angle formula? sin 2θ = 2sinθcosθ I was recommending the book to you as you can see from its fron cover, Levi sets out to do physics instead of maths and develops some fascinating and ingenious ways of connecting well known Maths theorems to the physical world. I though you would be interested. The only part of the extract is the picture moving the pole round the corner. The rest of the text is not relevant. I have uploaded the spreadsheet by adding .txt to it To return it to xls, remove the final .txt and you can play with other values The base distance, b, is input into box F1 so it can be changed for other distances. slope.xls.txt

Have you now ignored abandoned this thread ? If not, referring to the wagon wheel like diagram in the top right, Which colour is meant to represent the wet and which the dry ? You appear to like patterns and much interesting art has been derived from scientific use of drawing. Have you looked at Philip Ball's books, for instance The self made Tapestry ? https://www.google.co.uk/search?source=hp&ei=0rOZXZDGH6_5sAfr573oCQ&q=philip+ball+tapestry&oq=philip+ball+the+tapest&gs_l=psy-ab.1.0.0i22i30.176.5604..9600...0.0..0.540.2984.12j6j2j1j0j1......0....1..gws-wiz.......0i131j0.l6KipzJHdRw

Did I not mention at least a couple of times that an object with zero mass, such as the rod, has zero KE ?

Last night's response was rushed. Upon rereading your opening post I wonder if you are thinking that adding some acid phthalate to sodium hydoxide turns the sodium hydroxide into a new standard solution. That is not the case. What you are doing is 'standardising' by titrating a sample of it against a known (stable) standard viz the phthalate. Once you have made this measurement you know the concentration of the remaining sodium hydroxide almost as accurately as that of the calibrating phthalate. The solution of phthalate plus hydroxide that results from your titration is not the new standard solution. This new standard solution contains only sodium hydroxide (and water) and reacts with hdrochloric acid in its usual way.

I owe you a complete apology because I did not read your opening post properly and thereby misunderstood it. So I charged off in the wrong direction and in particular said there is no solution. Of course there is a solution. However the good news is that all was not wasted because my Physics approach was basically correct. As you said this is an interesting problem. +1 for that It is interesting because the Physics can help the Maths And the Maths can Help the Physics. Here is my revised analysis Going through it, First we establish the distance travelled down the hypotenuse, h , by simple trigonometry. (Maths) Then we establish that same distance from kinematic considerations. (Physics) Then we equate the two (Maths) Then we substitute values for the acceleration noting that the component of vector quantity a down the slope is given by g sinθ (Physics) A bit of mathematical manipulation leads us to the bottom equation for t2. (Maths) Now the answer of a Physicist who does not want to do calculus might look at this equation and say "If t2 is a minimum then t is a minimum at the same point or value of θ 4b/g is a constant so the minimum occurs when sin2θ is a maximum Drawing up a table of values of sin2θ as on the right tells me that this happens at around θ = 40o Or I can plot these and get a more accurate answer at 45o." (Physics) Our Mathematician on the other hand may well differentiate the equation to find that same minimum at dt/dθ or d(t2)/dθ. (Maths) We can plough through that maths if you like. This is not quite the brachistochrone problem since the curve is given as a straight line and so the acceleration is constant and we can use a simple kinematic equation. Finally since you like this sort of thing, have a look at the book by Mark Levi https://books.google.co.uk/books/about/The_Mathematical_Mechanic.html?id=lW5vQK6Tcu8C&printsec=frontcover&source=kp_read_button&redir_esc=y#v=onepage&q&f=false Here is an extract from his chapter on maxima and minima