studiot

There is a wealth of good useful information in your post, but I think you need to reconsider this bit. An ion is formed by the addition to or subtraction of one or more electrons from a neutral atom or another ion. This is more than just jumping from shell to shell this is a complete dissociation from or association into the atom or of the electrons. The moving elctron can be free or can be part of another atom or ion before the ionisation. Note since you can add to or subtract electrons from ions as well as atoms you can in fact start with a neutral atom and end with an ion or the other way round you can start with an ion and end with a neutral atom. Shell to shell transitions result on the absorption or emission of a photon of EM radiation.

This site draws better pictures than I do and answers a few more questions as well. https://byjus.com/chemistry/shapes-of-orbitals/

+1 for spotting that. You have just discovered 'modular numbers'. Also called 'clock numbers' https://en.wikipedia.org/wiki/Modular_arithmetic

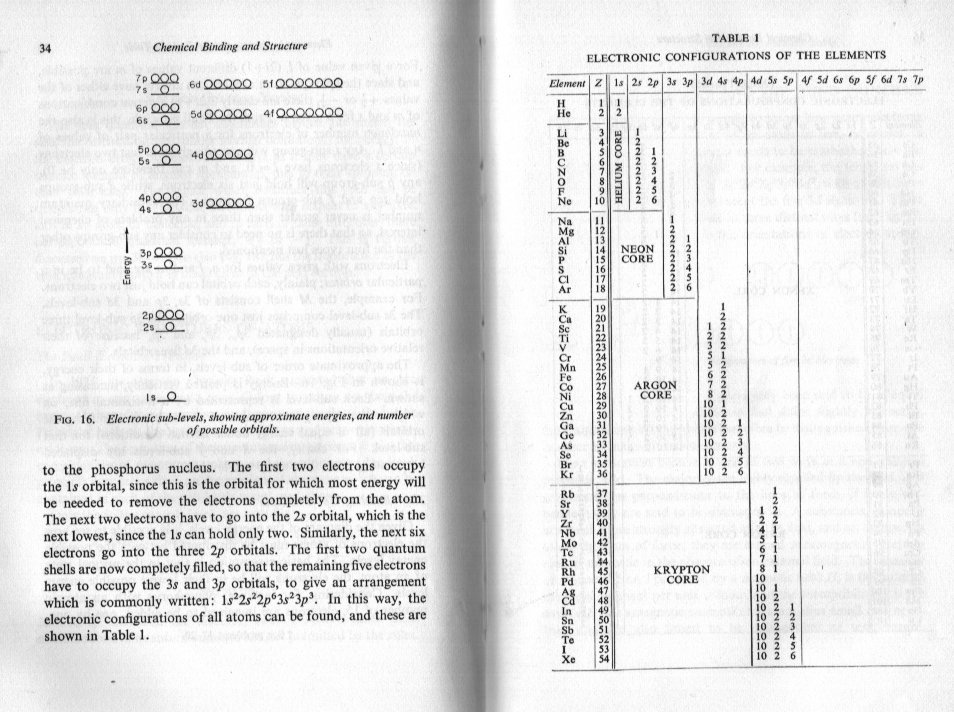
It's good that you are puzzling it. That is a step towards working a bit out for yourself which you have now done a couple of times. I try to leave some easy bit like that but I never object to you asking like this if you need more. The first shell (no 1) has only s one 's' subshell; no p, d e or f The second shell (no 2) has one 's' subshell and actually 3 'p' subshells; no d e or f The third shell (no3) has one s subshell, 3 'p' subshells and 5 'd' subshells; no e or f If you look at the left hand page - fig 16 - this is not only an energy diagram of the relative energies of these subshells it also shows you how many there are in each main shell (count the circles). The text also describes the standard method on writing these., where it syas 1s22s2 2p6 etc; the superscript is the number of electrons in the subshell eg there are 6 electrons in the 3 number p subshells in each main shell. Sorry I don't have time for pictures now as to how these numbers arise, other than to say it is because of the shape of the subshells, perhaps next time.

No, most definitely not. The nucleus is about protons (and neutrons) Ions, chemical reactions and bonding is about electrons. The nuclear structure does not change in the formation of ions or in other chemical reactions or or chemical bonding. The tables I posted are about the electron structure. The core is the electron structure of the inert gas. See the title of the table. Remember we mentioned these gases in a more simple way some posts back. So it works like this. Look at the top of the first table to the first 'block' There are just two elements in the 1s shell hydrogen and helium. This shell has only room for 2 electrons. We have already said that hydrogen has 1, and helium has 2 electrons. Helium is the first inert gas. The second block is Lithium (Li) to Neon (Ne) Neon is the second inert gas and note the core is labelled Helium core. That means that these 8 elements (yes including the inert neon) have a full 1 shell plus extra electrons in the 2 shell, but no electrons in 3 shell. Repeat Neon has a full 2 shell but not electrons in the 3 shell. The next block - sodium (Na) to Argon (Ar) works the same way populating the 3 shell (but not fully since there is now another subshell labelled 3d). This block is labelled to have a neon core Does this help ?

It is good to have another member of the staure of swansont making comments here. Just a few points to add. The electron has an electric charge of -1 and the proton has an electric charge of +1 Hydrogen has one electron and one proton; helium has two electrons and two protons. So the hydrogen ion (the atom with the electron removed) has a charge of +1 Helium has two electrons and two protons The the helium ion (alpha particle) with two electrons removed has an electric charge has a chrage of +2 As swansont noted the hydrogen ion (which is very common in chemistry and responsible for acid - alkali reactions) doesn't remain alone for very long before it is attached to something else. In water for instance it attaches to the nearest water molecule to form what is called the hydroxonium ion. This ion therefore has a +1 charge with a chemical symbol H3O+ As regards shells. There are two shell theories. There is an electron shell theory, which is what you have been discussing. And there is a nuclear (or proton) shell theory to explain how the nucleus fits together. As regards the electron shell theory, it is probably best to take a simpler approach as in the attachments. Chemical reactions occur between some of the electrons of the participating atoms and molecules. The atoms are regarded as trying to get to a configuration of a nearby noble or inert gas. This configuration is called the core configuration . The extra electrons are the one or ones that participate in chemical reactions and chemical bonding. But the wrinkle is that the 'shells' have a substructure, labelled s, p, d , e and f These are called orbitals. and the energy levels of these do not follow in a nice sequence because we now know that the shape of these subshells and indeed the shells themselves are not arranged in nice expanding spherical shells. Wiki has some nice pictures. There is some ovelap. Also I have been avoiding responding about Newton's cradle until you have finished wandering around the galaxy. It is rather complicated but an excellent introduction to several ideas we have yet to look at, including what is called the coefficient of restitution. Really the analysis depends upon this as to whether it is regarded a elastic or inelastic or something inbetween.

I think perhaps you are mixing up the three different meanings of the word inverse. The inverse is the result of the operation of inversion or the verb to invert. First definition:- to invert means to turn upside down. For example the inverse of [math]\frac{5}{{13}}[/math] is [math]\frac{{13}}{5}[/math] This definition has no meaning for simple numbers alone, you require a set of fractions or quotients to make it work. This definition has more importance when we use algebra rather than just number. For example the inverse of [math]\frac{{2a + b}}{{{b^2}}}[/math] is [math]\frac{{{b^2}}}{{2a + b}}[/math] Every fraction or quotient has an inverse in this sense. Second definition:- For any number or expression a the inverse is another number or expression a-1 from the same set such that a x a-1 = e Where e is the identity element of the set and a-1 is the multiplicative inverse of a. For example [math]\frac{13}{{5}}[/math] is the multiplicative inverse of [math]\frac{{13}}{5}[/math] and e = [math]\frac{{1}}{1}[/math] The inclusion of an identity element is important in defining a group, ring or other algebraic structure. But it does not guarantee the existence of a multiplicative inverse for all the elements. For example consider the set of 2 by 2 matrices. [math]\left[ {\begin{array}{*{20}{c}} 1 & 2 \\ 3 & 4 \\ \end{array}} \right][/math] Has a multiplicative inverse since [math]\left[ {\begin{array}{*{20}{c}} 1 & 2 \\ 3 & 4 \\ \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - 2} & 1 \\ {\frac{3}{2}} & { - \frac{1}{2}} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \\ \end{array}} \right][/math] So the multiplicative inverse is the matrix [math]\left[ {\begin{array}{*{20}{c}} { - 2} & 1 \\ {\frac{3}{2}} & { - \frac{1}{2}} \\ \end{array}} \right][/math] and the identity element is the matrix [math]\left[ {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \\ \end{array}} \right][/math] However not all sets have an identity element. And the identity element may not work with all members. The matrix [math]\left[ {\begin{array}{*{20}{c}} 1 & 2 \\ 3 & 6 \\ \end{array}} \right][/math] Has no multiplicative inverse. All the examples so far have been unary operations. That is operating on one single element of the set. We must now extend our definition to binary operations. Definition:- A binary operation takes two elements of a set and combines them to produce a single element of the set. Third definition :- The inverse of a binary operation means the reverse or undoing of the 'forward' operation. The example already given of 12 being the product of several different pairs of numbers that combine multiplicatively to yield the single element 12. for convenience 1 x 12 = 2 x 6 = 3 x 4 = 12 Now it can immediately be seen that this operation cannot be undone since there are three possible pairs that satisfy the forward operation so given the number 12 we cannot determine which pair was involved in the original operation. This lack of uniquness in the reverse direction means that 12 does not have a binary multiplicative inverse. This has importantance in prime number and factorisation theory. Genady's example only works backwards if we exclude 247 x 1 = 247. This is often done in elementary treatments.

Which comes back to my still ananswered point. What else is required to complete the analysis ? +1

If the government imposes an unfair Tea Tax ? 😀

'All' is too bold a statement, which if true would have precluded many discoveries in Physics. For instance the discovery of the nucleus by Rutherford. Or the discovery of the pattern of reversing magnetic stripes in the rocks at the bottom of the atlantic by Morley, Matthews and Vine. There have been many such breakthrough experiments and insights in scentific history.

Totally agree, but more to the point, what is this 'reality' ? Surely we can only offer our best effort to measure something and say If you do this in this particular way you will find the following happens.......

Trying to be a smart alec about this is really counterproductive as well as being somewhat insulting. You clearly haven't read many of my posts or you would know that I don't subscribe to the string hypothesis. As a mathematician I would ask if you have any real idea what a field is because my idea is very different from yours and furthermore there are many posts in many thread here where I have explained my pov. What is there to 'explain'. Theory and observation have coincided ever since the idea of a speed limit was first mooted and Maxwell suggested that light travels at this speed from his equations. Well since mathematically warping is the wrong word no I don't. This leaves only one question that of action at a distance, which I agree with you has yet to be explained by any hypothesis.

What make you so sure there is more fundamental physics to discover ?

Hasn't this thread wandered way off topic. What does it matter to the headline question how the next breakthrough arrives ? Surely the question is about when it will happen.

Incident means incoming as in artillery shells aimed at you by the enemy. Although this is not wrong, it is not the whole truth. A vibrating object posseses energy by virtue of vibration, regardless of any other energy it may also possess. In order to vibrate the object must accept energy from somewhere. That energy can be delivered in two ways. Firstly By a single impulse such as plucking a guitar string once. If this happens the body will respond by vibrating at its natural resonant frequency. Secondly By a continuous input of energy at the resonant frequency or by series of pulses timesd to arrive (be incident) at the resonant frequency. I tried to describe this in my previous two examples. This is something quite different. It is actually called 'phase locking' or 'pulling of an oscillator' in electrical circuits. A biological examole would be the synchronisation of periods within groups of women living closely together.

Well I see you haven't visited for more than a month so perhaps you are not really interesed in your subject. I was going to ask if you were thinking of applying for some sort of applied physics course but looking at the widely spread sunject range of your postings I really can't guess where you are going with this. Have you never been to the doctor or the pharmacist ? My local district hospital has a department of medical (applied) physics. You won't get very far with MRI or tomography or Chemistry in general without physics. How about the Earth Sciences - oceanography, geophysics, etc. Or the rapidly developing biophysics. What about physics in art? There is significant overlap between the sciences in general and even other subjects like art for applied physics to apply to all sorts of activities other than engineering. Ring wearing engineers ? I know of an (electronics) engineer at Marconi, who lost a finger in a radar beam, due to wearing a ring.

Ok so a set is just an imaginary container we use to collect together items/objects of interest. The simplest mathematical set is just a list of the (mathematical) objects in it. These are called the members or the elements of the set. Since some sets are very large indeed (even Infinite) the list can be very long or even never ending. The next step up (mathematically) is to collect together objects with some property to cope with this because if we can specify the property we only need this specification to specify the set. We can do without the list. For example { The set of all even numbers} We write the set in between curly brackets. But mathematicians prefer formulae to words so we write {x : x = 2n where n is an integer} To read this we say to ourselves (The colon means 'such that') "The set of all x such that x = 2n where n is an integer" In fact we can shorten this using the set of all integers which is given the symbol Z {x:x=2n,∈nZ} Note some authors use Note some authors use a vertical line instead of a colon. [math]\{ x|x = 2n, \in nZ\} [/math] It is worthwhile knowing that there are some standard sets such as N the set of Natural or counting numbers Z the set of all integers (positive and negative) Q the set of all fractions R the set of all real numbers (decimal fractions) OK so we have some sets. That is all you need to know about sets to start with. Don't worry about all the stuff about Union, Intersection and so on. Now we can do three things We can consider actions from one set to another ie between sets themselves. We can consider actions between individual members of a set. We can increase the value of the set by creating a (mathematical) structure. We do this by specifying particular useful properties of the transactions between members as in 2. Now if you think about school arithmetic we learn how to add, subtract, multiply and divide. This gives us four rules, called Paeno's Rules of Arithmetic. Three very useful additional rules are that Every possible sum or product between members of our set are also members of our set. There are no members which are not a sum or product of other members. Each sum or product refers to exactly one other member. When we have a set that conforms to not only the ordinary rules of arithmetic but also those three rules we call our set a group. Now going back to actions between sets themselves. Sometimes both the source and target set are the same or the target set is a copy of the source set. A mapping connects elements of one set to elements of another by means of some rule or process or formula. If every connection of the mapping connects to a unique (one and only one) element in the target set well call it a function. When this connection rule is satified we can also construct an inverse function. So for instance 1 x 12 = 12 3 x4 = 12 2 x 6 = 12 So given 12 we cannot determine which of these to claim as the inverse of the multiplication. That should be enough to start with.

Ok so a set is just an imaginary container we use to collect together itmes/objects of interest. The simplest mathematical set is just a list of the (mathematical objects in it. Since some sets are very large indeed (even Infinite) the list can be very long or even never ending. The next step up (mathematically) is to collect together objects with some property to cope with this because if we can specify the property we only need this specification to specify the set. We can do without the list. For example { The set of all even numbers} We write the set in between curly brackets. But mathematicians prefer formulae to words so we write {x : x = 2n where n is an integer} To read this we say to ourselves (The colon means 'such that') "The set of all x such that x = 2n where n is an integer" In fact we can shorten this using the set of all integers which is given the symbol Z {x:x=2n,∈nZ} Note some authors use Note some authors use a vertical line instead of a colon. [math]\{ x|x = 2n, \in nZ\} [/math]

Just a little bit of help here. Charmap Many of the symbols used, including the square root sign, are not available on the ordinary keyboard but can be obtained using charmap if you are using Windows (any version) In later versions just type charmap into the query box and press return. Boxes like these should open up. https://www.bing.com/search?q=charmap+symbols&form=WNSGPH&qs=SC&cvid=0f0cbd2b7805469e9dcdfe1e8cfc51c4&pq=cgarmap&cc=GB&setlang=en-GB&nclid=74D28496F4DE45C06BECB76344916980&ts=1731258460021&wsso=Moderate You can then scroll up and down. Select a particular character Copy it and paste it into your text. Extra hint It often pays to select several special characters and paste them in and add one more step Delete the ones you don't want at any one place.

Did you also catch the bit about the forcing function ? A vibration can 'bang between hard stops, for example a car bonnet or a door or other fixed panel can bang in the wind again its restraints, alternately hitting one then the other. On oscillation reached the end of its travel naturally as it runs out of one energy (the energy of motion or kinetic energy) because the oscillation is transferring the KE to potential energy. In a system with not losses that cycle is repeated endlessly PE → KE → PE → KE...... In a system with energy losses, often due to friction, (called damping) the energy gradually leaves the system. Newton's cradle is not relly a simple oscillation it is actually quite complicated as one side is free to go as far as it likes, but the other side has a nearly hard stop.

Please make up you mind and also revise your terminology. x, y and z are not parallel they are orthogonal variables. That is why they are independant.

I wasn't suggesting you go self study those subjects, I was offering help with that. However it is laudable that you took the interest to look these up and also to indicate where I should start. +1 I have some apple trees to prune this afternoon ,but I will make a start when I have done that.

I don't think either the untimely demise of either Galois or Abel stopped their genius flowering. They had both achieved much before that. There were plenty of Frenchmen who started well but lost in one of the many french wars. I agree with that, But not this Depending upon your POV, rampant poverty is still true today.

Actually (pun intended) both were 'low church' middle class and fairly well to do. De Morgan studied under hamilton and Airy from at Trinity College Cambridge from the age of 16 whose main interest was economics (though Wiki has not picked up on that) Bayes main interest as a church minister.

Or simply went on to other things than Science, as with Bayes or DeMorgan. Of course there have been evil geniuses in the past like Cardinal Richlieu or Rasputin.