studiot

Your words were So I offered you a source who did exactly that. Detailed discussion of the relationship between Maths and Physics is complicated and extensive and off topic in a subject about the direction of time. So I was brief. Similarly here is a note to Michel The Ancient Greeks had a Philosophy of "ideals" which linked the physical world to the theoretical world. This reappears in modern algebra a generalisation called the theory of ideals.

Read this https://books.google.co.uk/books/about/The_Mathematical_Mechanic.html?id=lW5vQK6Tcu8C&printsec=frontcover&source=kp_read_button&redir_esc=y#v=onepage&q&f=false

Only waves can diffract. As noted, diffraction of electrons is a manifestation of the wavelike characteristics of electrons. Changes of direction of an electron considered as a particle is called scattering. There are various forms of electron scattering. See here https://en.wikipedia.org/wiki/Electron_scattering

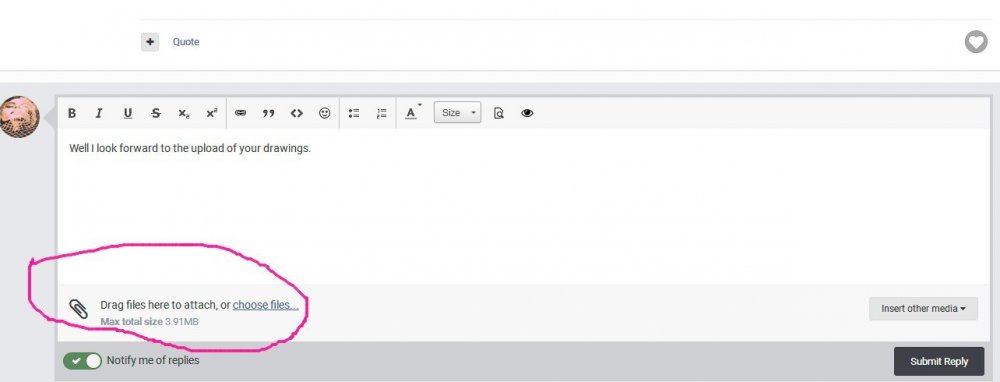
Well I look forward to the upload of your drawings. Since you are having trouble with this, look at my uploaded picture (screenshot) It's very easy - I have circled the place to look. Click on 'choose files' and follw the instructions - it will search your computer for your drawings. Once they are uploaded, place the cursor in your text where you want to insert them and just click on the assembled image at the bottom. As regards your idea of comparing gravity with electrical forces. This is already done in very elementary work. But this only gives us electrostatics. All the dynamic effects need an electric theory quite different from that of gravitation. Have you considered this?

Don't forget it is only a small part of a much wider system of (Newtonian) mechanics.

Well Bell is aware of the problem, as were Lawvere, Bishop and the authors of my extract, Hellman and Shapiro. As far as I am aware all use a scheme (with variations) that runs as follows Postulate an 'extended' set R (usually extended with infinitesimals of some sort) Postulate a suitable set of axioms to deduce the properties that are inheritable in R alone Show that the usual rules of calculus work in the extended set Use the axioms to transfer this to claculus in R. Unfortunately the notation and language employed is not universal - even the word Language is given a special meaning So this means that a new language needs to be learned to appreciate each one. Here are some references. Non Standard analysis - Martin Davis (book) SIA - pdf http://pi.math.cornell.edu/~oconnor/sia.pdf Classical continuum without Points -pdf https://pdfs.semanticscholar.org/af2b/ca15dafc01a38c7fe7a8142b9a407d57b244.pdf Bell of course you already have. This is remarkably similar to what I say to people about the application of Vector Spaces to physical problems. That it is not a matter of a simple map from one set to another, but that a third set needs to be involved. Perhaps this will be the way forward. Finally you shoud beware of the use of the following symbols Δx; δx; dx and D(x) These are used somewhat inconsistently to my way of thinking

I don't know since you haven't told me. But whether you use (x+dx) or (x+2x) or (x+anything that is not a real number) is irrelevant until you justify what arithmetic you are using that permits this and defines what the result is. Do you consider (x+dx) to be a real number or what? You are still missing the points of the questions I am asking. Since it is your proposition it is for you to state clearly the system of algebra (and its rules) in which you are working. SIA has problems of its own. Here is an extract from a recent paper. Mathematicians have struggled with the philosophic problem of dealing with this for centuries, but no one has yet come up with a watertight answer, or a better one that the limit process which has many other uses to boot.

Thank you for that bit of arithmetic. I was not enquiring about this. Sadly you have completely misunderstood my question and points. Perhaps this was my fault for not being detailed enough. You have used the arithmetic operation " + " (amongst others) My consideration concerns whether this is indeed legitimate and, if so, in what system of algebra? Consider this: If I work with the set of integers the axioms guarantee that use of the three operations, addition, subtraction and multiplication will result in another member of that set (ie another integer). eg 10+7 = 17; 10-7 = 3; 10 * 7 = 70 all work fine and are well defined. But 10/7 is not defined, and further, reciprocals do not exist in this algebra. Equally the sum (10 + 10/7) is not defined in this system Now you have the sum (x + 2dx) which begs two questions How is addition defined in your working? How is multiplication defined in your working? In other words which system of algebra (arithmetic) are you working? This is necessary since you cannot be using the standard axioms of arithmetic.

I was in two minds about continuing this discussion. However although you belatedly (second post) announced that you are considering dx as an 'infinitesimal', you still haven't clarified first opening post. What type of algebra are you using that allows you to write f(x + 2dx) ? What makes you think that this exists? Can you point to a theorem that supports this view?

Because by and large most scientists are resonable men and women, who are often concerned with the truth as best they can. But two questions Do you place your most reasonable men as linebackers in (american) football ? Are politicians noted for being truthful folks ?

I wasn't aware that there is currently an EU tariff of up to £60 per kilogramme on US cheese. I really would like to taste some of the good stuff- any recommendations? https://www.bbc.co.uk/news/world-us-canada-48915578

It is not clear to me why 3 more dimensions than the ordinary 3 are needed to describe this situation. So how does the need for 6 arise? I also note that conventionally reduction degrees of freedom reduces the number of dimensions. For instance the contraint x2 + y2 + z2 = r2 reduces a manifold from 3D to 2D. I also do not understand this relationship. What does "compacted dimensions leaving the string or transiting the string mean"?

Well first thoughts on your thread. I respectfully suggest you narrow the focus down some. As it stands the subject is enormous - far too big and diverse for one thread. You have concentrated on the Americans, but say you are moving to Europe. You will find matters quite different here. Europe has a long tradition of state sponsored scientific establishments, that have waxed and waned in importance over the centuries. The UK was the exception. Until the end of WWI, the main impetus was privately developed (sometimes will royal encouragement) and quite a different structure developed. The only real exception came from a military direction. The fifty years following WWI saw the establishment of state scientific undertakings such as the Road Research laboratory, The Building Research Establishment and many others. Sadly during the following fifty years governments of both 'right' and 'left' have steadily dismantled / privatised these operations as well as the ones with military beginnings such as the Hydrographic Office of the Admiralty and The Ordnance Survey. The histories of the Hydrographic offices of the UK and the US are interesting to compare. I once read a book about the sporadic history of the US version and how it suffered from political interference and being a politcal football. The UK HO by contrast enjoyed substantial government support from the 1690s to the 1990s. Significant also is the difference between the US, the UK and European systems of professional qualifications. Most former British Empire states more or less follow the UK pattern, Except India, where the state has stepped in.

Thanks for the translation. It is very useful. I think it would be good to bear in mind that this is an introduction to the subject and also intended to be a lead in to indirect methods e.g. using Hess's Law. The calorimeter offered is very basic. As I said there are several types of calorimeter including fast calorimeters. https://www.springer.com/gp/book/9783319313276 That said, your book makes good points that many chemical reactions are complicated by side reactions, or are multistep so that one step happens very fast and another relatively slowly. If you want the individual heats for each step this can be tricky to measure. Perhaps other members here can contribute soemthing as well ? +1 for the effort you have put in to holding a good discussion. Here are a couple of points about Chemical themodynamics teminology you might like to keep in mind for the future. 1) Be sure about the difference between forms of energy, heat and work. They are accounted separately in Thermo. 2) An endothermic reaction refers to heat absorbed not energy absorbed and an exothermic reaction to heat evolved, not energy evolved. 3) Be aware that there are different sign conventions for energy accounting. Chemists use the simplest and most logical. Engineers and some Physicists use an older convention from the days of steam engines which leads to different signs in some equations. The Chemists' convention is simple: All forms of energy evolved (heat, work etc) are counted as negative. All forms of energy absorbed (heat, work etc) are counted as positive. Using this convention the First Law says ΔE = q + w Where E is internal energy of the system q is heat absorbed by the system w is work done on the system = - (work done by the system) ie is negative if the sysem does work. Hope this helps.

You have posted this in the Physcis section, rather than the Philosophy section so I take it you are looking for a Physcs answer. The question is "nothing" even possible?" is really for the philosophers. A hard bitten Physicist will say that "'nothing' certainly exists." She will say "hey look I can use a chunk of "nothing" to complete my capacitor." "I have two charged plates so all I need is some "nothing" to keep them apart and I have a capacitor!" Empty space has properties, not least permittivity .

To help you make sense of things try this. (1) Consider f1(x) = mx where m is a constant. So f(x) (are you comfortable with this notation?) is directly proportional to x and the plot is a straight line through the origin. (2) Now consider f2(x) = mx + c where c is another constant. This plot is also a straight line, but not through the origin. Comparing For (1) if we multiply x by another constant say a then f1(ax) = a f1(x) for example, if m = 3 then at the point x = 2 f1(x) = mx = 3*2 = 6 and if we now double x so a = 2, at the point x = 4 f1(x) = mx = 3*4 = 12 So f1(2x) = 2f1(x) But compare this with f2(x) with c = 5 and m still = 3 at the point x = 2 f2(x) = f2(2) = 3x + 5 = 3*2 + 5 = 6 +5 = 11 and at the point x = 4 f2(2x) = f2(4) = 3*4 + 5 = 12 + 5 = 17 So f2(2x) is not equal to 2f2(x) Mathematically we say that So f1(x) is a linear function and So f1(2x) = 2f1(x) is the condition for it to be linear. The function f2(x) is called an affine function.

Remember I am trying to keep it simple to bring out the important points. So I am only going to consider frames that are not in relative motion with each other. So any frame has an origin. The the coordinates of the particles m1 and m2 are x1 and x2 in our original frame, call it the x frame. If we now refer to a second frame, call it the x' (x prime) frame, whose origin is at x0 in the original frame then x1 = x'1 +x0 and x2 = x'2 +x0 Now we have the force = mass x acceleration and acceleration is a function of the x coordinate So Force is proportional to the x coordinate in our original frame F = F(x1 , x2) Which is two equations [math]{m_1}\frac{{{d^2}x}}{{d{t^2}}} = F = F\left( {{x_1},{x_2}} \right)[/math] and [math]{m_2}\frac{{{d^2}x}}{{d{t^2}}} = - F = - F\left( {{x_1},{x_2}} \right)[/math] Which expresses the proportionality of force with acceleration in our original frame (the x frame) But if we substitute the transformations to cahnge to our second frame (the x' frame) we have [math]{m_1}\frac{{{d^2}x'}}{{d{t^2}}} = F = F\left( {x{'_1} + {x_0},x{'_2} + {x_0}} \right)[/math] and [math]{m_2}\frac{{{d^2}x'}}{{d{t^2}}} = - F = - F\left( {x{'_1} + {x_0},x{'_2} + {x_0}} \right)[/math] Now we see two things. 1) The equations now depend upon the origin of the coordinate system loosing homogenity along the x axis. 2) The equations violate the Principle of Relativity since this law of Physics no longer has the same form in both coordinate systems. And all we have done is transported (translated) the whole system along the x axis, nothing is actually in motion. How we fix this is the subject of the next installment. And yes, thus far we are still Newtonian mechanics. Even in his day they were aware of the problem, but sidestepped it. It was the second postulate of Einstein that was revolutionary.

Thank goodness your English is excellent. I can see from your page where is says that Enthalpy depends on temperature and pressure. And that some reactions may be 'incomplete' in that further reaction is possible such as the combustion of carbon to form carbon monoxide (partial or incomplete) or carbon dioxide (complete). of course the incomplete product is itself combustible. But I cannot see where is suggests that Enthapy depends on the speed of the reaction. Perhaps you can point this part out? There are several types of calorimeter. Perhaps the special type used to measure the Enthalpy of combustion was not invented in Hess's day. This type of calorimeter is called a 'bomb' calorimeter. These are fired by an electric element to complete the reaction quickly.

I would be interested to learn more of this, particularly the context. Can you post a scan or photo of the page ? What is the textbook please?

You haven't explained it to me once yet. That miscounting is taking lack of mathematics too far. Reported

@Edgard Neuman Are you proposing to address my questions?

Brownish?

Yes this is good stuff, but we need to do more. Since it is going to be raining all afternoon I will take the opportunity to expand on my equations. Whilst you are waiting I suggest you consider the idea that Force is a function of position, x. (rather than comparing two accelerations) So what happens if we choose different one-dimensional frames?

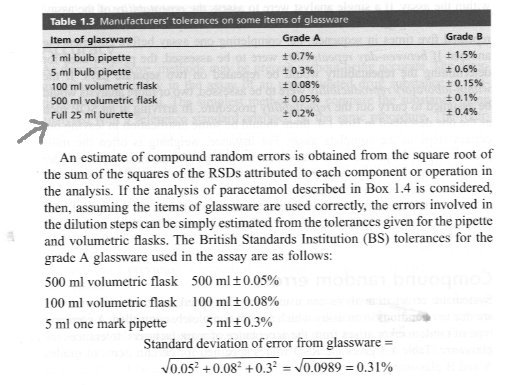
(1) Yes, see this extract from the latest version of 'Pharmaceutical Analysis' by Watson. Note the tolerance on the entry for the burette. As a matter of interest what tolerance would you ascribe when the buretter reads 0.00? Would you allow a negative volume?

What do you mean by interactions? Would you accept the action of a single particle e.g. (spontaneous) emission I offer this because it is the easiest to wrok out. If you must have multiple particles have you looked at scattering?