studiot

This is clear unadulterated rubbish. A single particle (you did say' an') or a single anything else cannot be in superposition with anything else, since there is nothing else to be in superposition with. It takes two to tango.

With a properly developed and nurtured ethic, that appears to have withered some in the last few decades, I consider blind reviewing should be unnecessary except in a minority of cases. One practice I noticed with papers has been the great increase in statistical methods employed by writers with insufficient statistical maturity to discuss or defend the results so obtained. I think this is because many place now have 'works statisticians' who do the actual analysis or supervise the entry into compute programs the writers cannot understand by themselves. This is then compounded by peer reviewers who may be the world's experts in the subject matter of the paper, but still not savvy staticians. We can't, after all be good at everything.

This is now the third time of asking my question about your view on superposition. Since you are in clear breach of the rules here by not offering any sort of reply, despite plenty of opportunity, I will be reporting this thread for closure.

For what it's worth, my understanding of the Zeroth law is that it introduces the three important equivalence relations into thermodynamics thus: Consider 3 separate thermodynamic systems, Z1, Z2,and Z3 (we use Z to avoid confucion with entropy) 1) Then if Z1is in equilibrium with Z2 and Z3 is also in equilibrium with Z3 then Z1 is in equilibrium with Z3 ( This is the transitive property). 2) Z1 is in equilibrium with itself (reflexive property). 2) Z1 in equilibrium with Z2 implies Z2 is in equilibrium with Z1 (symmetric property). These assertions can be used to show that thermodynamic temperature is a property of a system and was originally proposed by Maxwell under the title the Law of Equal temperatures (1872)

Yes, it's true that if you physically change the system, the new system can have greater entropy than the original. The original system can never gain entropy if isolated. Do you understand why this is and that this is why the old formulations were made in terms of cyclic processes?

Another first rate model, +1 keep them coming please.

This thread was inspired by the following comment in this query about air conditioning. But is that so ? The change in entropy going from state A to state B is always the same, irrespective of the path between A and B since entropy is a state variable and thus a function of the state of the system alone. It make no difference whether that path is reversible or irreversible. Only in the case of a reversible path is the entropy given by the expression [math]\Delta S = {S_B} - {S_A} = \int_A^B {\frac{{dq}}{T}} [/math] In order to calculate the entropy change for an irreversible path we must find an alternative reversible method of going from state A to state B and then use this to calculate the entropy change. For any completely isolated system we are restricted to adiabatic processes since no heat can either enter or leave the sytem. For a reversible process in any such system dq=0, hence ΔS is also zero, which means that S is a constant. Thus if one part of the system increases in entropy another part must decrease by the same amount.

Yes you were very polite, but how is your German ? Here is the original statement of the second law. I think that of its own accord is a very reasonable translation of von selbst, don't you? However this is really off topic here, as is your version of the Second Law. I did (politely) suggest that you offered your own answer to the topic. Since discussion of the issues surrounding the Four Laws is worthwhile in its own right I have started a separate topic for this, in the Engineering section, where I believe discussion of air conditioning systems also belongs.

By all means provide a better explanation of your own if you think mine was inadequate. (Note I threw the original post together in a hurry whilst the OP was still online.) The second was added later by way of further explanation. Is the average room an isolated system? Since the example you give is a non equilibrium system any heat transfer will soon cease, and is not applicable to the OP electrical generation reuqirments. Note the word I missed out was continuously so "heat will not flow continuously from a colder body to a warmer one" is more accurate. Why bring entropy into it at all? "of its own accord" Anthropomorphic? or just jolly and colloquial? Well more formally (an including the continuously) "without external effect" But your system is isolated so there are no external effects. It is very easy to get tripped up by all the ifs and buts in thermo.

So are you going to answer my question?

The zeroth laws says that to transfer heat you must have a temperature difference. The second law says that heat will not flow of its own accord from a colder body to a warmer one. And, of course, your walls are warmer than the air you are trying to cool.

I'm tempted to ask if you know what superposition means. The equation is simply that if 2 effects, call them A and B, act on something together then the combined effect (call it C) follows the equation C = aA + bB where a and b are simple constants. This technique is very heavily used in classical amd macroscopic Physics, Chemistry and Engineering.

John is quite right what you propose would breach the Laws of Thermodynamics. Additionally light energy is not the same as heat energy, which is why there is not an equivalent heat to chemical energy converter, as there are light to heat converters and light to chemical (potential) energy convertors. Thermodynamically energy comes in various grades or a heirarchy with heat energy the bottom of the heap. The use of energy requires converting energy from a higher form to a lower form and all forms eventually end up as heat. These facts are embodied in the zeroth and second laws of thermo.

"They don't cover each other 100%." So you actually agree with me. Why didn't you just say so instead of arguing the examples from where they do not overlap? To move on here is an interesting (mathematical) example (not of symmetry). Consider the sequence {1, 2, 4, 7, 11, 16 ...} This can be generated in a variety of ways, For instance by noting that the difference between succeeding terms increases by 1 each time Or by using the formula Pn = (n2 + n +2) /2 for n = 0,1,2,3.... Both use a 'rule' and so can you class them as regular? But the exact same sequence could be the output of a (perfect) random number generator. So would the output then still be regular? The whole question of regularity, symmetry, pattern is absolutely fascinating, both in abstract thought and Nature. A superb book that discusses this in lots of different ways is The Self Made Tapestry - patthern formation in Nature. by Philip Ball

I will put this down to a momentary lapse of memory, because actually you said exactly that in so many words. I further gave you a simple example of something (in mathematics) that is irregular but symmetrical. So can we stop this dancing around and pursue a proper discussion?

In particular, if I draw something on a sheet of paper is that "in Nature" or not, setting aside whether it is regular or irregular?

This whole argument over definitions is fruitless as such arguments tend to turn out. The whole beauty of the English language is that it has so many words with similar meanings and even substantial overlap of meaning. This is because there is so many subtle variations of meaning available. So arguing that one such word is identical to another leads to such fruitless discussion. That is why it is important in analytical discussion and (since you want to remain in Maths) exactitude, it is important for the promoter of the discussion to be clear as the his exact usage of language. You have used three such words Regular, irregular and Nature. We are all still waiting for your input on these. I note that wtf has used a different meaning for Nature than swansont.

+1 I believe the forum uses the same counting app that a certain politician uses to count his votes and discount his opposition's.

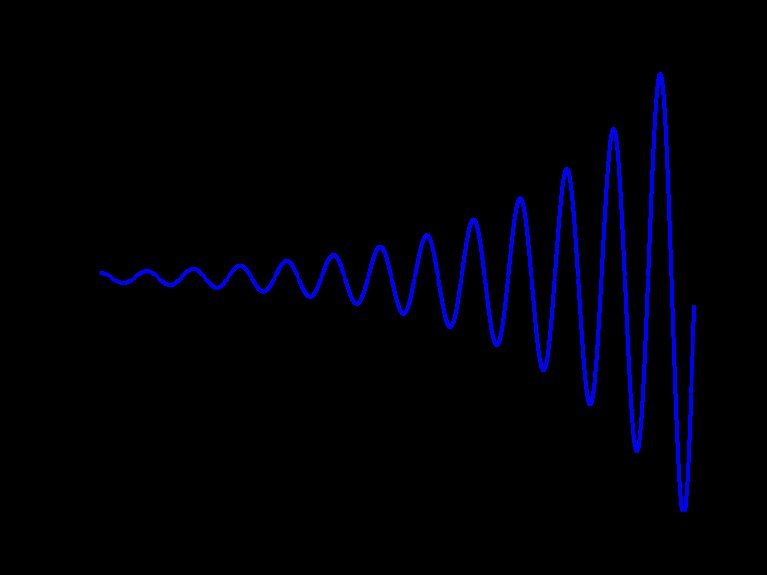
You are wriggling. If this is true then you can state what those functions might be. Not that this is relevant since what I am showing you is complete in itself. I will tell you that every single one of those oscillations is unique and not one of them is symmetrical since the scale is continuously changing on both axes. That is both the period and amplitude of the oscillation is continuously varying. A full isosceles triangle is symmetrical but can be decomposed into two smaller triangles, neither of which is. So what.?

Can you do two things? Put the numbers in order, writing them in two columns like this Number Instances 3 1 4 1 5 3 6 1 8 1 Now you must have been given definitions of median and mode Compare these with the data in the columns.

Better to type in "methanol and cupric oxide" https://www.google.com/search?client=firefox-b&ei=NwvcXPe7AbHzxgOs8obgBA&q=methanol+and+cupric+oxide+&oq=methanol+and+cupric+oxide+&gs_l=psy-ab.3..0i22i30.152328.177874..181186...0.0..0.146.3558.37j6......0....1..gws-wiz.....0..0i67i70i251j0i67j0i131i67j0j0i131j0i10i67j0i13j0i8i7i30j0i13i30j33i22i29i30.9Pr9Xyq7Wh4 This gives lots of stuff including the comaprison of copper and chrome oxides as catalysts https://www.researchgate.net/publication/231366160_Complete_oxidation_of_ethanol_acetaldehyde_and_ethanolmethanol_mixtures_over_copper_oxide_and_copper-chromium_oxide_catalysts It does seem you have to heat the methanol over the oxide. Unfortunately so many sites these days want to collect personal data an put up a barrier until you agree. So I leave and never return.

To emphasise the difference between symmetry and regularity and to further link this to your new question about rules, here is a graph. I think it is regular because it follows a define formula, equation or rule (note rule and regular come from the same Latin root). Do you think it is symmetric?

Have you considered the solubilities (not necessarily in water) of cuprous v cupric oxides? eg in Fehling's solution/test.

Firstly it should be pointed out that different disciplines use different words for the concept of 'laws'. So we have rules, principles, axioms, laws, and so on and so forth. But what is important is that none of these apply to all matters at all times. They all come with the small print 'domain of applicability' which, like all small print, is far to often ignored. So for instance logic circuits in electronics are binary right? That is they operate on being in one or other of two electric states, commonly called 1 and 0. But whilst there is an enormous welter of circuit matters and theory, the plain fact is that electronics engineers have thought is necessary to invent a whole new area, outside the binary domain. This can be seen by looking in a catalogue of logic chips and discovering that there are many 'tristate' chips. So my answer is something may be 'more fundamental' if it is relevent but maybe totally irrelevent. So tell me, Is Fermat's principle more or less fundamental than Kepler's laws?

Saved me the bother of another disregarded reply. +1 Instead I will vote to draw the veil on this thread please, moderators.