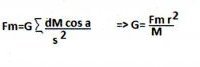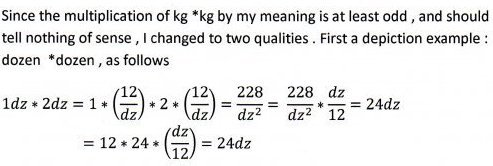studiot

Have you learned nothing in the last 10 years here? You must, for instance have seen the long thread debunking the lake Balaton nonsense. You started here harping on about gravity in 2009 and you still appear to be promoting unsupported nonsense about it. You seem only to have found a way to tweak sirswan's beak, or did you not read the red moderator notice closing your last thread?

Hey you are correct, I was wrong, but you don't need to go to the trouble of calculating N. you can use [math]\frac{{{P_1}{V_1}}}{{{T_1}}} = \frac{{{P_2}{V_2}}}{{{T_2}}}[/math] to obtain [math]{P_2} = \frac{{{T_2}{P_1}{V_2}}}{{{T_1}{V_2}}}[/math] directly. Well done both of you, +1 each.

Not really. Addition and multiplication are both closed in the complex plane. Neither form of 'vector' multiplication is closed in the plane. In fact there is no axiom at all in the vector space space list for multiplication of a vector by a vector. This is why you can say that C is a vector space, and a field, but the planar space spanned by a pair of non parallel coplanar geometric vectors is not. Note I also said geometric vectors. However what I said stands I think that geometric (pointy) vectors are confusing enough here, without going to the full complexity

No this is wrong. What did you use for N?

Your physical analyis is correct (I haven't checked the arithmetic) provided that beta is the volume coefficient of expansion, not the linear coefficient. https://opentextbc.ca/physicstestbook2/chapter/thermal-expansion-of-solids-and-liquids/ Also provided that it is permissible to ignore the expansion of the steel box (steel has a significant expansion coefficient). I agree that the oil can be regarded as incompressible so the air 'takes up' all the volume loss due to expansion. So now you can calculate the volume of air by subtraction in both the cold and heated conditions. Then you need Boyles law Pressureoriginal x Volumeoriginal = Pressurecompressed x Volumecompressed It is probably easiest to work in Bars which makes the expanded pressure equal to Pressurecompressed = Volumeoriginal / Volumecompressed since you started with 1 bar of pressure. Does this help?

Firstly I would avoid using vectors as analogies. The geometric vectors Eise is talking about are not the same as complex numbers. The two possess some common features but there are also differences. If the goal is to model one with the other, obviously this can only be done for models only concerned with the common features. However the differences are important here. In particular there is only one rule of multiplication for complex numbers, but there are two quite different forms of multiplication with vectors and neither correspond to the multiplication of complex numbers. This, of course, is why we have both of these. As regards the second question. Map, yes, tabulation, yes. Let us just use the integers for a minute. Using these we can construct 'pigeonholes' There is even a theorem called 'the pigeonhole principle'. https://en.wikipedia.org/wiki/Pigeonhole_principle (For once the Wiki article is accessible to those without a triple Phd in maths.) We can regard the coordinates as identifying a particular pigeonhole, rather than a length. It does not matter what 'size' each pigeonhole has or even that they are square. One pigeonhole is one pigeonhole. And we can put anything we like into it. So we could put the product of the x and y coordinate in there. This does not mean that this product equals an area. In fact in this model there is no such quantity as 'area'. However our pigeonhole array forms the multiplication table or tabulation I referred to earlier. Note also that Wiki goes further and discusses the case where some pigeonsholes have multiple occupancy. We want to specify for our purposes that each pigeonhole has exactly one thing in it. This can be developed further to give meaning to your idea of crossed imaginary axes.

I was going to say that electric cars with no battery have been around a long time. Even the late victorians/edwardians had them. But Carrock beat me to it. +1

Stubbornness is not a problem. Oranges and apples are as they cloud the issue.

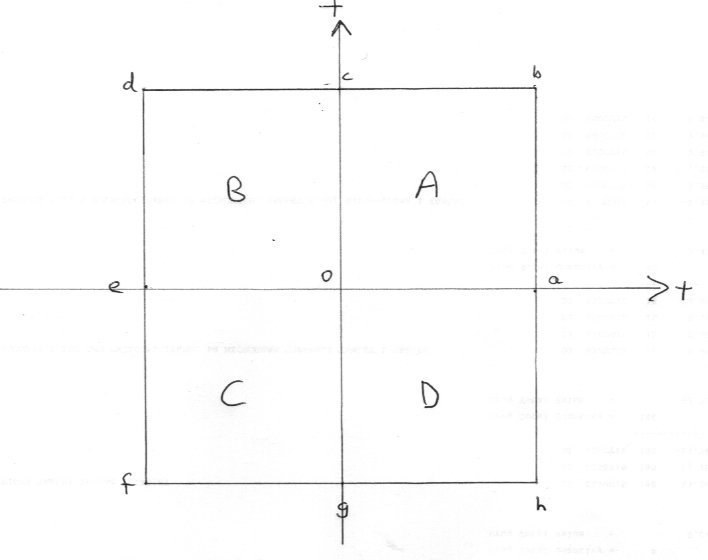
I hoped you would spot my non deliberate error here Very sorry for this I was rushing again. Those in zone A are of the form +x + iy Those in zone B are of the form -x + iy Those in zone C are of the form -x - iy Those in zone D are of the form +x - iy Bloody editor just cancelled my previous edit What do negative oranges look like? And what useful properties do positive and negative oranges have , mathematically? And what does an area of 3 x 2oranges mean? Perhaps the graph or plane is not the right way to look at counting oranges? The point of introducing the symbol i is that is is just one extra symbol that has very desirable properties. There is another way of looking at this plot, that I wasn't yet ready to introduce, lest it confuse the issue. The plot is then not a graph but a tabulation. It then makes sense. Do you wish to digress to explore this option?

By the two graphs I assume you mean your original pair, one with both axes real and the other with both axes imaginary. The short answer is that since ,as you rightly point out, you have no common axes the only way to make a new graph is to draw a four dimensional one. No so good huh? Now in drawing this one you have a standard graphical representation of a complex number (not not an imaginary one) with one real axis (the x axis) and one imaginary axis (the y axis) To answer the other questions, 1) Zone A is now neither positive nor negative. Complex numbers can not be positive or negative. The only use of + and - is to denote direction along the axes. 3) Points in all four 'zones' are complex numbers. Thos in zones A and B are of the form x + iy Those in zones C and D are of the form x - iy This is the form we use to perform arithmetic with a complex number. (It is called complex because it is made of more than one part - 2 parts) There are other forms of presenting or representing the any given complex number. Your second is used for plotting on diagrams (graphs) and is of conventional plotting representation (x,iy) The whole plane is called the complex plane. 4) Answered at the beginning of my answer to question 3 I feel we are making definite progress. Note there are several other ways of representing a complex number, each with its own special points. They are all equivalent. I will not confuse things by introducing them at this time.

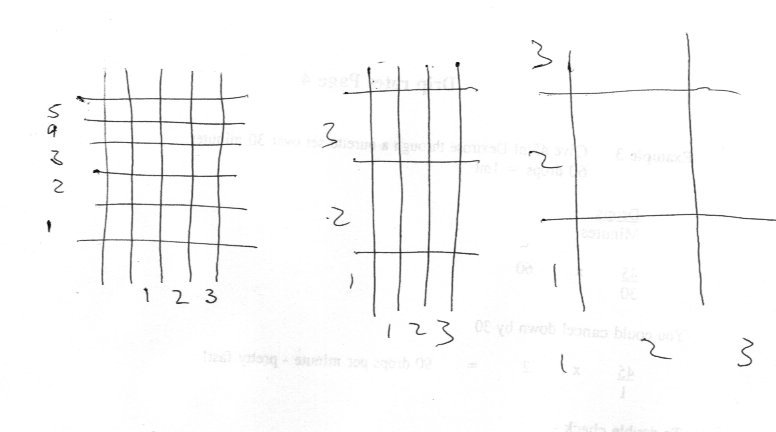
Eureka ! The world is saved and we do not need to reinvent the wheel or redefine i and arithmetic works. It works like this. Michel both your diagrams are correct. But your interpretation needs a little help. They are not multiplication diagrams. To start with your green and yellow squares using real numbers. The area of the square is the length of one side times the length of the other. It is not the product of two coordinates. You are mixing up corordinates and lengths. In you opening you have correctly introduced directions showing a positive and negative direction. length is defined as the difference of two coordinates, taken in a consistent (positive) direction. length = most positive coordinate minus the least positive coordinate. So the length of both sides of the green square is (+1 - 0) = +1 So the area of the green square = (1-0)(1-0) = +1 The length of side of the yellow square is [0 - (-1)] = +1 So the area of the yellow square = [0 - (-1)] [0 - (-1)] = (+1) (+1) = +1 Exactly as in your diagram. So the arithmetic for the real numbers follows the rules of arithmetic for the real numbers. No suprise. On to your second diagram. So the length of both sides of the green square is (+i - 0) = +i So the area of the blue square = (i-0)(i-0) = i2 = -1 The length of both sides of side of the yellow square is [0 - (-i)] = +i So the area of the yellow square = [0 - (-i)] [0 - (-i)] = (+i) (+i) = -1 Exactly as in your diagram. So the arithmetic for the real numbers follows the rules of arithmetic for the real numbers, provided that i2 = -1. What you have done wrong is to say that the length of side the yellow square is -1 and of the the red square is -i. This effectively reverses the direection of measurement, making your working inconsistent. This can be even more dramatically brought home by the following diagram. Clearly the area of the large square bdfh is equal to the combined areas of the four smaller squares, A,B,C and D. But if you count these areas as positive and negative you will find the Area of the large square is exactly zero ! You can confirm this by comparing the measurement of side lengths by your method and by my proper one. I have not put numbers along the axes, as you can work this out for both 1 and i in order to convice yourself.

That doesn't work since the product of two imaginary numbers is not an imaginary number. You can't make (1i *1i) = -1 without the i by that system. Prefixing an undefined label to every real number certainly retains the field struture of the Reals. But would be just a pointles as prefixing the label 'real' to every number in the field. You have not created the extension field gained by adding the special properties available in adding one special symbol with the properties of being the square root of negative 1. This particular extension field is of course called the complex numbers. A few posts back, I gave another example adding a less controversial number - the square root of 2. That creates a proper field.

Can't see how that is compatible with the vector space axioms. Further in all the treatments I have seen, ix an behaves as if it is a perfectly respectable product. How can ix be 'only a name' ? How can you do mathematics with 3 * (only a name) or 3i * (only a name) or (only a name)* (a+ib) ? What on earth does the field set look like?

Thank you for your answer. So this mains electricity runs your appliances and aircon and so on, and you would certainly notice the effect if you stuck your finger in the socket. yet the average voltage in an AC supply is zero. This curious fact is a real world example of a phenomenon similar to what you are seeing on your plots. The area under the power curve is also exactly zero over one complete cycle. Don't worry I wasn't looking for you to post the answer, just discover for yourself that the second is the square of the first and the first is the square of the second. There are many strange things in Maths, which has led some to the occult.

Thank you evrybody for your thoughts. I didn't realise there were so many money making scams masquerading under the banner of Science. It saddens me that there is one more thing to beware of. In the days when I wrote papers, I trusted the hosting organisations not to do this.

There is no conflict. nor is the underlined bit always true. What do you think 0i * 0i makes? This might help. Humour me and answer this question please. What is the mains voltage in your house? You might also like to try the following What is the square of [math]\frac{{ - 1 + i\sqrt 3 }}{2}[/math] and now the square of [math]\frac{{ - 1 - i\sqrt 3 }}{2}[/math] Do both and see if you notice something very interesting. (Note I have put the i before the [math]{\sqrt 3 }[/math] to make it clear that the square root sign does not apply to the i. If I put is after as in 3i it can be confusing as to whether the i is inside or outside the square root.) But if you really don't like complex numbers you can try another similar type of compound number, but using only real numbers, of the form [math]\left( {a + b\sqrt 2 } \right)[/math] I await your answer with interest.

Can anyone comment on the provenance of this 'journal' ? It promotes this rubbish for instance (Aug 2018) https://www.scitechnol.com/peer-review/gravity-is-a-myth-CHpy.php?article_id=8027

But Michel doesn't want to do this. He want to use only imaginary numbers and that is where his problems start. Technically by themselves imaginary numbers do not form an 'algebra'. Of course, both the real numbers and the complex numbers do. This issue is so fundamental that we normally take it for granted and don't bother to mention it or state it. We just so used to cracking on with appropriate mathematical object we don't even realise we are automatically selecting them. Using only only imaginary numbers doesn't lead to mathematical nonsense, it is just a helluva lot more restrictive than the alternatives - as you rightly observe Michel is finding out.

The eco (furniture) factory described in the book is still going strong. https://grimshaw.global/projects/herman-miller-factory/

Which Lagrange theorem would that be? The one in Number theory? or The one in Group theory?

No work is done unless a force moves its point of application.

I think this argument about point masses is a red herring. Whether a body is a sphere or not, it has a centre of mass. Mechanics requires we use this centre in our formulae. The (solid) sphere is just one of the easiest for calculation.

The fact that the Earth is spinning affects both the magnitude and the direction of the attraction experienced by any body in the Earth's gravitational field.

This is just plain bad mathematics. This definition and argument is circular This is only true if G is constant, something you are trying to disprove ! You are relying on the constancy of G or T in any summation or integral where you take G or T outside the summation or integral. If they are not constant, then your calculation would be different. It is very difficult to separate out calculations involving G and T from your pictures, since you have mixed them intimately.

I agree with this, unfortunately those promoting these shifts tend to be less well resourced and less articulate than the establishment. For example the small book 'Cradle to Cradle' by Braungart and McDonough Is very well reasearched, and contains some excellent examples of actual (successful) cases. However it is very hard to read as its style is not coherent or progressive. When our back have been to the wall (eg WW II) coherent (joined up) Government did indeed lead and direct a successful collective response to an emergency. But real and imminent emergencies do appear to be the only drver for such action. In the Netherlands (Holland) last year the banned the use of gas in new homes. The UK government is considering a similar ban. But another part of the UK government is still offering grant suport and promoting gas boilers. Worse the UK government has fragmented its policy to provide a relaible and stable electricity alternative.