studiot

Surely a definition is only of worth for the purpose for which it is made? Clearly it must be fit for that purpose. It surely cannot be guaranteed for any other purpose. So here, a definition of mass must be made fit for purpose by posing it in a way that can be included in mathematical derivations employing it. Any other theoretical considerations are irrelevant.

+1 (I like the rest as well )

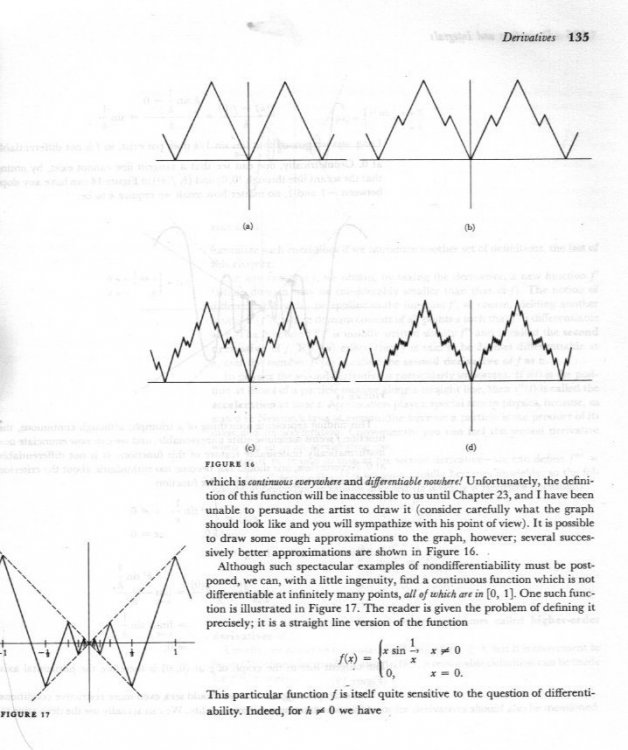
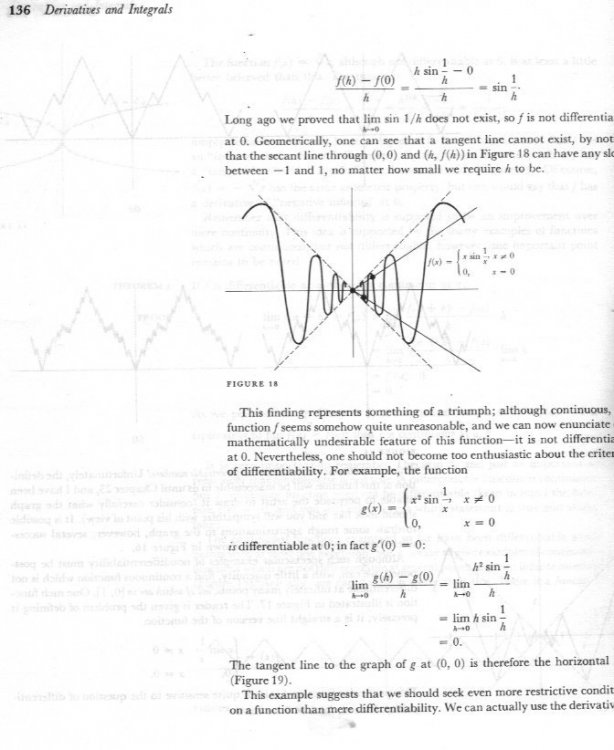
Read these three pages from the gold standard in the subject at this level (Calculus by Spivak) Better still, buy the book and read the whole of it several times.

What does that mean?

That is for you to show, it's your presentation. How does it lead to the derivative for say the modulus function y = |x| Or perhaps for a cusp?

Thank you , I take it this was a yes to my question? To do this you need to show that infinitesimals (which is the mathematical name for what you are describing) can be summed as you show. There is nothing in the normal rules of algebra to allow this. This is just about the stage reached by the ancient Greeks, and it led them to Zeno's paradoxes.

Or are you actually referring to the meniscus line?

I am not (yet) arguing anything. I am simply seeking clarification by asking a question or two. I may be barking up entirely the wrong tangent. A diagram or three from the OP would help the presentation and probably shorten it considerably.

Do you mean something like this?

I couldn't make your algebra consistent. What for instance happened to r2 in your equation 1? Please demonstrate a proper algebraic chain of reasoning.

Thanks.

Of course learning is easier in your native language. I will try to remember that English is not yours. I have said that the images are plots or graphs of functions. You said, quite forcefully, that you wanted to discuss the wave function. I do not know why it is so important to you to classify phenomena as waves or particles. Can you tell me? To be so definite you have to know what a wave is and what a particle is. How would I know if I met something in the street whether it was a wave or a particle or something else entirely?

The wave function itself is not a probability; calling the square of the wave function a probability is an interpretation. So the next important thing to understand is this. All the probabilities about something must add up to 1. So the probability of heads plus the probability of tails for a coin toss is 0.5 + 0.5 = 1. So when we interpret the square of the wave function as the sum of all the probabilities about it must add up to 1. For a wave function, interpreted as a probability plot, this means that we take add up all the values of the raw calculated wave function (squared) from Schrodinger over the whole domain and scale the total to 1 to make this so. This process is called normalisation. The value of the normalised wave function (squared) in any small region within the domain is then the probability of finding the energy or particle in that small space in any one measurement. I do not know if you understand this adding up process - it is called integration?

Of course they do. If you shine a light on something is gets slightly warmer as it absorbs photons. In turn that something warms the air in contact with its outer casing.

I'm sorry I calculated the wrong dimension. I should have calculated your dimension as 43 feet minus 16 feet 9 and a half inches (rounding the 9-sixteenths). So your rectangular box is 8 feet by 26 feet 2 and a half inches.

1) Your chain of reasoning was limited to a binary choice. Why? There are multiple postulable origins and multiple postulable processes of selection. 2) Why would I refer to the supernatural, since JC had already done so and I don't agree with him, especially on a Science site? 3) We have only recently gained the means of modification by genetic manipulation but, as others have also pointed out, selective breeding has been practised for a long time. Further consider the taboos "Thou shalt not marry thy sister/mother etc" Do herds or packs of wild animals obey this maxim? 4) Selection is also about 'deselection' ; survival of the fittest implies perishing of the weakest. 5) You posted a general statement about style in English to which the answer is no, even if the qualifier is actually redundant, which it is not in your example. 6) On The Origin of Species is reckoned to be one of the most readable, if not the most readable, scientific treatises of all time. I understand this was by Darwin's design. Have you read it? Chapter 1 is all about selection under domestication Chapter 2 is all about selection under Nature (The environment) Chapter 4 is all about natural Selection and its comparison with So can you tell me where Darwin discusses the supernatural? It is always useful to avoid the trap of misquoting this wonderful document, either in its Title (as is often done) or in its body text.

Well I think some qualifier is useful, if not essential in the phrase "Natural Selection". I fear you have fallen into the old trap of assuming binary choices (either ...or...) If it is not 'this' it must be 'that'. What about "self selection" for instance ? As I understand the theory, "Natural" refers to selection during the to the normal everyday environment and the selection it produces. It does not refer to unusual or special environments (accidents) that may only occur once or to specially arranged environments such as human crop selection etc. In any event, in my view, it is worthwhile to distinguish between different filters.

[math]16ft\;9\;and\;\frac{9}{{16}}of\;an\;inch[/math]

A neat way to put it, do you have any references to follow up? +1

Thank you for this reply. I have been putting my time here into a couple of other threads, but I need to push on here as well so I had crack on. I fear you are still looking at things in the order N1, N2, N3. You also worried about circularity of the definition of mass, which is why I included the opening paragraph in the Stanford discussion on Principia post in the now defunct thread. I have underlined why they think no circularity arises from mass = volume times density. Density in those days (like other mathematics) was comparative. They really meant the density compared to a standard (water) i.e. specific gravity. This was because they wrote in terms of ratios and proportionality. When you make the comparison you end up with a ratio of ratios and the standard cancels out. This exactly the same process to move on from ratios of accelerations to atios of masses. This is achieved by introducing a third body to the other two already noted, and comparing the acceleration ratios agains each of the original two. That is all I have time for tonight, the (still simple) maths follows next.

Goodnight then. Perhaps tomorrow we can see what it means that the Schrodinger wave function "extends over the whole domain".

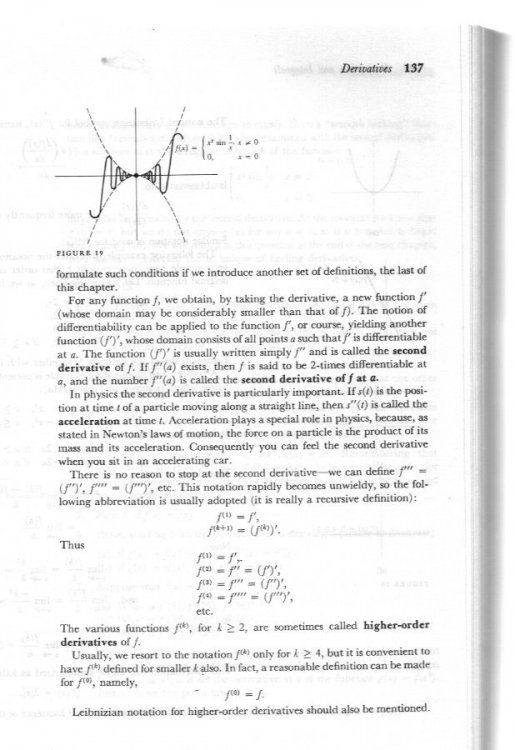
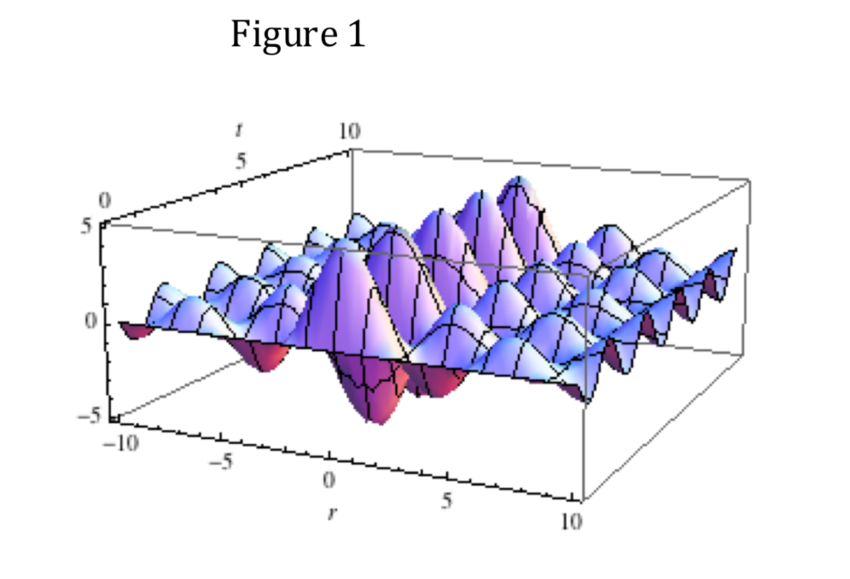
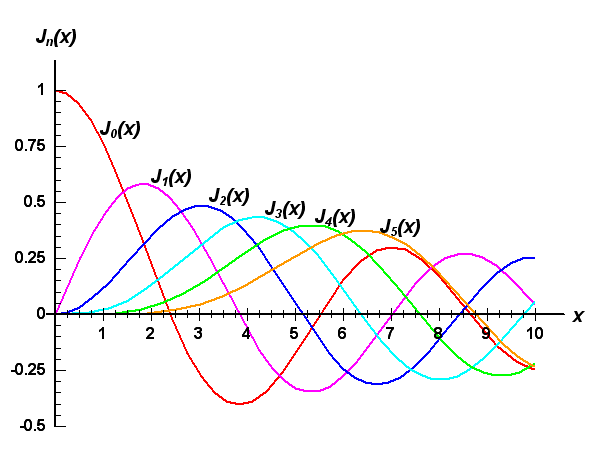
Yes indeed so to look into it further: A function uses a mathematical rule to process values of one or more input variables (perhaps in combination) to generate values of an output variable. The collection or set of all the possible values the input variables may take on is called the domain. This rule applies to every value in the domain, even if the result is a null (zero) value of output. The function itself includes every input and output value and may be plotted as a graph. The foregoing images are graphs of functions chosen to illustrate particular points. In the the first one the domain is the whole of the positive x axis (although only part is shown). The image shows a whole family of functions called 'Bessel functions' shown in different colours and labelled J0(x), J1(x) etc. Each one is different and the difference depends upon circumstances. These circumstances are reflected in the form of the rule for calculating the output. So the Bessel function J0(x) is the red curve. And the function is the whole of the red curve. I cannot stress enough how important this is. These are one dimensional functions. The second plot are also Bessel functions but are two dimensional because there are two input variables. And the 'curve' is now a surface. A wave function (Schrodinger or classical wave) is essentially no different. The wave function extends over the whole domain. But there is not one wave function it is a whole family of curves, each different depending upon circumstances. Armed with this knowledge it is possible to proceed to examine them and their properties.

Has this question now been answered? Do you understand what a function is? Here are a couple of images

How can anyone tell if you are right or wrong when your posts are so lacking in specificity. There have been many different double slit experiments, studying many different properties and phenomena.

You should ask a magician , not a mathematician such a wide open question.