studiot

Thanks to all those who replied and tried to help. I mean the Belling-Lee connector. https://en.wikipedia.org/wiki/Belling-Lee_connector

Does anyone know when and if the bog standard TV coax plug has changed its specification or better can provide any dimensioned drawings? It a long time since did any wiring of coax aerial cable but I have a box of coax plugs and other fittings from the mid 1970s (new). Needing to wire up a new TV and aerial I fitted these to new cable and plugged in the aerial. The TV steadfastly refused to acknowledge the aerial and I noticed some trouble plugging in. Sourcing some modern new coax plugs and fitting one of these resulted in immediate life in the TV. So I inspected the older plugs and compared them with the newer ones. Average centre pin diameter for older ones 2.9 mm Average centre pin diameter for newer ones 2.21mm Both measured with the same micrometer. Small wonder I was haveing trouble plugging in. Looking on the net I can't find any reference to coax plug sizesor standards and no longer have any trade datasheets or other sources available.

Thanks, but you haven't explained the area question. Further suppose we consider the path ABACADAEA. This encloses zero area, althoug it is not the shortest. Again suppose we remove C, D and E so we only have AB. How much area does the optimal solution enclose? And since n now = 2, your formula becomes No of paths = 2!/2*2 = one half. What is one half of a path? My formula, by contrast reads number of paths = (2 - 1)! = 1! = 1 path, which I think to be correct.

I still don't understand you reference to area. Particularly if minimum time is required. Can you please demonstrate it with reference to the following diagram. Can you also show any difference between starting at A,B,C,D or E? Just list the node sequence will do.

No, parallel transport refers to translation, not rotation. I mean the connection of vectors (leading on to tensors) to 'hyperspace', that I am reluctant to expand on here

I can't find it either, but I have given up finding old threads on this 'new improved' Scienceforums. Yes that thread does contain a hint before that long exposition from Xerxes, but is not the one I was thinking of. I think it would be too far off topic to reproduce the presentation here, but if you would like to start a new thread to discuss what happens when you place a vector at some point in a vector field and then try to rotate it we could try again there.

My understanding of the distinction between ductile and brittle materials is that a ductile material has a significant plastic region in its stress / strain curve, whereas a brittle material does not. This means that a brittle material is unable to redistribute its maximum stress plastically and so cracks at the point of maximum tensile stress. This can lead to what is known as fast fracture or just standard brittle fracture depending upon the nature of the load and the material. This behaviour is important in structural engineering and strongly temperature dependent, which is important in geology and metallurgy.

I suppose that depends how you define evolution. I see no maths in your proposition. Further you are talking about a more general usage of 'evolution' than the specific theory mentioned in your title. So which is it?

Yes complex numbers could be so classed, though they would not normally be referred to in this way. Multiplication by 'i 'can be regarded as a rotation through 90o, to 'somewhere' Bthe out of the original domain (in this case the real numbers) This is where the classification scheme becomes a bit murky because it has grown up from disparate sources. Because the complex numbers are numbers in their own right. But also generalised coordinates are a linear construct, which is why they are favoured for computer implementation. We have for variables X1, X2, X3.......Xn. which fully describe a system The generalised coordinates are aX1 + bX2 +cX3 +...... Where a, b, c... are coefficients (numbers real or complex) This is linear and can easily be handled in computer form. If a, b, c... are allowed to become functions in their own right then the construct becomes non linear and we have a sort of generalised 'generalised coordinates' I do believe I have tried to explain (to you) before how this applies to cartesian vectors ( in Euclidian space), perhaps you are ready for it now?

What do you mean by area? I thought you had come from a programming background. There is a certain method known as Little's algorithm https://www.google.co.uk/search?q=little's+algorithm&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&dcr=0&ei=k6hQWozZI4X98weZ_oXIBA But it may be "expensive computationally". There are (n-1)! possible paths in a network with n nodes. There are also methods that may well produce the correct path, since the minimum is often (but not always) Hamiltonian. Since there are also allied network tour 'problems' such as the 'postman problem', it would also be good if you would clarify your question.

No and yes. The method is known as the method of generalised coordinates, and is tied up with 'degrees of freedom'. No because it does not, of itself, introduce any method that is the only way of doing the calculations. Yes because it is sometimes the most practicable method, especially with a computer since it is basically an array (matrix) method. However we have become very cunning in reducing the calculation burden by the clever use of physical knowledge. For instance with my skater we can remove an entire (vertical) dimension if we do no allow her to jump. As regards classical spin generalised coordinates, the full works would introduce moment of inertia and products of inertia and an axis of spin that can point anywhere in 3D. Happy googling on those terms.

The method basically means (in this case since a version is used in many branches of Science) Compute the time for every possible path. Identify the minimum. Two points. I said the algorithm can be refined. There may be more than one path with the minimum time. There may be no minimum (all paths have the same length)

Since you have posted this in computer science, There is a valid mathematical method know as 'the method of exhaustion' The method can even be refined to shorten it. Which will completely satisfy your question.

The moderator suggested we limit the discussion to classical phenomena. I usually use classical phenomena because I try to find examples the OP may have personal experience of and are simple to compass. Remember also that analogies are never exact.

The point was about the observer, not the frame. Classical observer observe different wave speeds depending upon their own speed. But once an emitter has launched the classical wave into the medium, it looses all control.

Are you sure? I thought the innovation was that the speed of light was the same for all observers. This is what distinguishes it from previous knowledge since in classical wave theory the wave speed depends upon the medium and is independent of the emitter.

Rob, you misunderstand me. Which surprises me because I have said enough times in this thread, that a dimension reuqires a scale, not a point number and that a point has zero dimensions. So 1 and 0 or 1 and -1 or 1/2 and -1/2 or the more complicated spins that Mordred mentioned don't cut it as a dimension in their own right. What I am saying is that there are more complicated objects that act at / interface with the 3D real word at one point that have many parts. A vector has two, but I doubt if the OP understands vectors so should I introduce them or worse cartesian tensors, the simplest of which have 9 parts (getting up towards strings there). Perhaps you would like to discuss spin in terms of the inertia tensor?

Glad we are getting somewhere. Physics is fun. So back to the skater. There is a difference between the spin and the position on the ice. We have a scale metres or whatever of across the ice and along the ice and a height scale when she jumps in the air. The important thing is that, like the length, breadth and height of the brick stack, along and across each require only one number on a scale. (Just like the thermometer scale I posted earlier) But spin does not take up any of these and further Whilst it is true that there is a scale of spin speed which only needs one number, Spin cannot be described in only one number. As the song goes, "it takes two baby" Because spin can be either clockwise or anticlockwise. So this is not even on scale. Further sometimes the skater doesn't spin about a vertical axis, but swings her legs about an inclined axis as she hops from one leg to the other. This is the simplest example I can think of of what I mean by something more complicated. So spin can only be completely described by an abstract concept, which has dimensions of its own that do not take up any space in the 'real 3D world of up, across and forward yet still interface with that 'real' world. Such dimensions are called sometimes phase dimensions and the space they occupy is called phase space. Because they are all made up abstract ideas there is not limit to the number of dimensions in phase space - it is just limited to you imagination and ingenuity. Hyperspace just literally means beyond (real) space. I have added the real in brackets because that is its usual meaning but some (such as string theorists) include abstract dimensions from phase space. As to the extension of 3D real space to 4D or 5D or more. Scientists have looked but can find no evidence for the existence of hyperspaces greater than 3D (ignoring time). One simple test is that just as 3D objects can obstruct the view of each other and reveal each other as they move in 3D space and also cast shadows on each other, so we would expect to observe the 3D equivalent if we were 3D beings embedded (note that word embedded) in a 4D real space. The lack of shadows is particularly telling since 2D beings could observe shadows cast by say the Moon or clouds on the 2D surface of our 3D Earth.

Excellent. OK so let's think of a stack of bricks. This has 3 dimensions in what we call ordinary 3D space. Length, breadth and height. I can choose to make my pile any combination of length, breadth and height I like. So if you tell me to make a stack of bricks I will ask, how tall, how wide and how long boss. 3 numbers, quite independent. And that is all that is needed to completely describe the stack. But Physics is more complicated than this. Some properties cannot be decribed by a single number and the activity of the skater is one such. As the skater moves about the rink, just skating along, 3 numbers will do to say exactly what the skater is doing. But as soon as she starts to spin, another property comes into play. No only can she spin but she can vary the spin by extending her arms or drawing them in. So we need additional data to specify her activity, including the extension of her arms. This type of data is a form of hyperspace that is superimposed upon normal 3D space, but does not use up one of the existing dimensions. The dimensions in String theory are similar. They refer to additional information to describe the 'strings'. I have to leave now but please ask away an I, or someone else will try to answer later.

Woah indeed, I'm trying to build up to hyperspace but I need to get the ducks in a row first. Please look at the question in my last edit as it leads directly to explaining the difference between string theory space, other hyperspaces and ordinary space. Here it is again. One question for you for next time. Have you watched skating demonstrations or competitions on TV or wherever? In particular have you watched the skater skating around, then spinning on the spot?

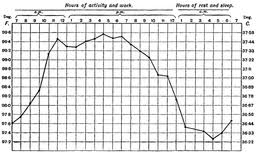
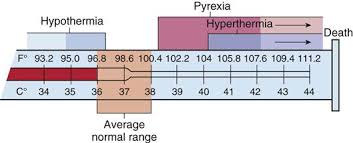
OK that's a useful reply. Science moved forward tremendously when the number zero was invented. A dimension is a scale against which we can measure some property of interest. (Sometimes we can measure several properties against the same scale.) So a single point is not a scale it cannot vary. We say it is of zero dimension. A line has one dimension. A sheet of paper has two dimensions, because we can show two independent scales on it. Note the word independent. This means we can choose any value from each scale, whatever the value of the other scale may happen to be. A sheet of paper with two scales is a graph or plot. Here are a couple of examples, of the same thing the range of temperatures for a normal human adult. Notice that we only need one number to specify an actual temperature so the plots can be one dimensional or two dimensional. We call the collection of scales we use the 'space' . One particular space is the one we live in which has dimensions of length or position. This is the one you are referring to, but it is not the one String Theory uses. That is enough to digest in one go so I will pause for questions. Edit One question for you for next time. Have you watched skating demonstrations or competitions on TV or wherever? In particular have you watched the skaterskating around, then spinning on the spot?

Good morning Pandothemic and welcome. Gosh string theory is heavy going and not for the faint hearted. As an amateur you need to be aware that scientists use ordinary words in very special ways and this can easily lead someone trying to misunderstand something a scientist has said so be careful. Here you need to understand what is meant by a dimension and a space in general as well as 'space' and dimension in particular. Do you understand the idea of graphs or plots?

Nobody has mentioned the difference between serial and parallel. We reached the technical limits of parallel over ten years ago hence, SATA etc.

It is interesting to contrast natural evolution with human development as processes that result in a more viable syste. Nature appears to use the scattergun approach. Try every possible variation and discard the failures (in large quantities). Human try to be more cunning and only try those variations with the greatest assessed chance of success (and not all of those either).

An excellent summary with a worthwhile comment at the end (underlined) +1 I can only add the observation that there were two Bacons dealing in Philosophy and Rob is referring to the second, as the contemporary of Galileo. Roger Bacon 1214 - 1292 Francis Bacon 1561 - 1626