studiot

Both have specific status amd meanings in Science, which are different from general usage. I hypothesis is a (hopefully) well thought out 'guess' or proposal. That is is is made for good scientific reasons. Once made the hypothesis is tested, preferably in many ways. If the predictions of the hypothesis conform to observation then it may be elevated to the status of Theory. If not it is rejected. Usually a Theory actually contains more than one hypothesis along with some development of their interactions and implications. Newcomers here sometimes fail to make this distinction and are marked down as a result. Does this help?

And use wolfram alpha to provide some known example results to test your program.

Do you know this website? Wolfram http://mathworld.wolfram.com/AckermannFunction.html By the way (BTW) since this is coursework we can't do it for you but we can hint and guide. However you must play your part and show some working. Also this should be in homework help.

The analysis commits the classic error of division by zero. Both the cosine and the cotangent are zero for angles equal to [math]\left( {2n - 1} \right)\pi \quad :n = 1,2,3...[/math] leading to division by zero in both the defining equations.

Some very good kitchen table descriptions here to take note of. I particularly liked the two above +1

Have you seen this? http://demonstrations.wolfram.com/ParametricEquationOfACircleIn3D/

Thank you for this, I will print it out to look at tomorrow. On first sight it appear more rigorous than this comment in your previous diagram/post There are no tangent planes in your diagram. A sphere has tangent planes, a circle has tangent lines.

Even with a much simpler shorter post you didn't read it properly. Like you my post mentioned four angles. Further it didn't say you didn't read my post it said you didn't read it properly. I didn't say it was. So what? I also asked a question about (the mathematics of) your diagram but instead of answering you accuse me of not reading your post. Considering I am not accusing you of being a crank but actually seeking to find out if you genuinely have a useful viewpoint to offer and trying to help you with it, despite your mathematical failings, this just extreme arrogance and disregard for others.

Keep probing. +1

Well I tried, even though I'm a bit sorry I bothered since you clearly didn't read my post properly. What do you think the black loop curve is in your diagram? Do you think that it could be used for spherical trigonometry?

Thank you for posting the asymptotic curve. Yes I often make this point that SR is undefined or unknown above c. Though I do not go as far as refuting SR. +1 There are other more prosaic phenomena in Nature and mathematics which show this behaviour (such as the specific energy line in fluids). These have more than one type of recovery once the critical value is passed.

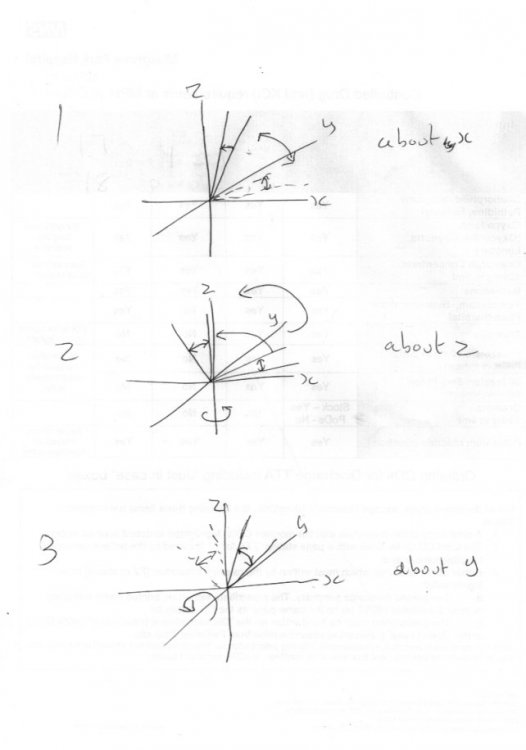
I wonder if this is a key to your difficulty. I have hastily dashed of some sketches as I had to sneak onto the scanner. Sorry for the lack of quality. Each of the three shows an angle as described between two straight lines in different orientations relative to ayz coordinate axes. Each sketch shows what happens as you move the pair of lines and their included angle relative to each axis, but wihtout changing the angle itself or the relationship between the pair of lines. I wondered if this had any bearing on what you are trying to describe.

rIsn't this veering off topic? A surface is a two dimensional object, insofar as it may or may not be embedded in a space of higher dimension. You have referred to projective geometry. One of the aspects of PG is that it is indifferent to distance. That is why a diagram of Desargues Theorem works. http://mathworld.wolfram.com/DesarguesTheorem.html

So far no one has ridiculed you, though you have been asked for more detail. A short answer is that yes in some circumstance there are (serious) applications of probability to the physics of time. For instance given the probability of the radioactive decay of an atom in a bunch of atoms, you can calculate the probability of simultaneous decay of 2,3 or more atoms. You can also discuss the meaning of simultaneous in terms of the time taken and the uncertainty principle. For a longer answer you need to propose a less flippant example.

Why is it so important to you that your expression be an identity? It may well be an expression that correctly models some phenomenon. But an identity relationship does not depend upon the use you put the expression to. Either the expression always equal one, whatever you use it for and it is then an identity. Or the expression doesn't always equal one, in which case it is not an identity. I am not sure what you are trying to achieve with this projective stuff. Can you elaborate?

Actually it doesn't. The equation actually shows that the relativistic mass v speed curve becomes asymptotic to infinity at the speed of light so is not determinable from that equation.

1) Why unfortunately? Is this personal? 2) No 3) Neither pzkpfw's nor Kodak's image formation on a screen show the screen at the focal distance from the lens optical centre. 4) I didn't suggest it did, I was going to post some very excellent pictures from Nikon about that. 5) If Kodak's calculation is correct (suprise suprise) why are you bitching about it? 6) It's basic that you can start a fire by focusing the Sun's rays onto an imflammable substance with a converging lens. That is what happens if you put the substance at the focus of the lens. A project wants to make the image (much) larger, a camera wants to make it (much) smaller 7) The focal distance is determined by the lens not the light approaching it. If Kodak say their lens has a focal distance of 86 mm I would rather believe them than you, without much stronger evidence than personal attack. I particularly liked this +1 and +1 tp pzkpfw for all the hard (and good) work put in on this thread.

Very smart. However, it's not how a lens forms an image, and it explains why this thread is getting nowhere. I think you misunderstand both Dalo and pzkpfw's diagram. Here is a kodak carousel projector calculator which shows the truth. For instance the focal length of a lens to project a 2m image on a screen 5 metres away is 86mm Kodak projector lenses are in the range 75mm to 200mm focal length, and zoom between these values to focus at a fixed screen. Note that projectors usually achieve Dalo's parallel ray requirement with a collimator between the light source and the slide. Note that projector greatly magnify the object in the mage, whereas cameras greatly reduce the object size in the image on film or sensor. Damm I lost all my text again https://www.digitalslides.co.uk/wp-2013/faq-items/what-focal-length-lens-do-i-need-for-my-slide-projector/

With respect, there's room for theory speculation? hypotheses?

Because Dalo want's to display an image on the screen, not burn a hole in it ??

Do not be modest about your diagram,. It is not only better than no diagram, it is perfectly fit for purpose ie adequate. So +1

[math]{\sin ^2}\nu + {\cos ^2}\nu = 1[/math] Is a trigonometric identity since there are no values of nu that do not satisfy the equality. So is [math]\sin (\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta [/math] again since there are no (pairs of) values of alpha and beta that fail to satisfy the equality. But there are still values of (triples of) alpha, phi and lambda that fail to satisfy your equation 6. So it is still not an identity. For instance put [math]\alpha = \frac{\pi }{4}\quad \varphi = \frac{\pi }{2}\quad \lambda = \frac{\pi }{2}[/math] Then your expression 6 becomes [math]{\left( {\sqrt {\frac{2}{4}} *\sqrt {\frac{2}{4}} } \right)^2} + {\left( {1*\sqrt {\frac{2}{4}} } \right)^2} = \frac{3}{4} \ne 1[/math]

What better place to start then the two books from the man who did the original experiments? The Mathematical Theory of Relativity Space Time and Gravitation. Both by Eddington Cambridge University Press.

You made an assertion concerning three numeric variables. You gave them Greek letters which makes writing about them more difficult, they could just as easily be called a, b and c or x1, x2 and x3. Whatever, fixing the first two has a greater impact than you think on the third variable, you call alpha. Fixing phi and lambda to the values I gave reduces alpha to numbers which make [math]\cos \alpha [/math] zero or the contents of the second brakcet cannot reduce to the square root of 1. There is only one value of alpha that satisfies this (along with its cyclic values). Dimensions have no bearing upon identities. Perhaps you should look up the meaning of the term in mathematics. Your formula is an equation not an identity. As such it has solutions for some phi, lambda and alpha, but not all.

Grease and oils form a barrier that is more easily removed by hot (soapy) water.