-
Posts
18486 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
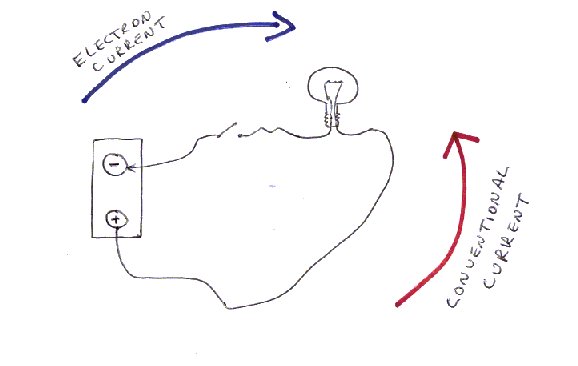
If you really want to look into electric sign conventions, then we should have a new thread. It would be a diversion here. So I will just put up one diagram and ask you to consider the terminals of a battery, particularly the negative one. When the switch is closed conventional current is said to flow around the circuit in the direction of the red arrow. No actual discussion of charge carriers is needed. The Disney fairy tale about electrons runs like Nellie the Elephant who packed her bags and said goodbye to the circus. So the tale goes that the electrons pack their bags and say goodbye to the negative terminal and go on their holidays around the circuit, arriving at the positive terminal. Question one As each electron leaves the negative terminal does that terminal become slightly less negative ? If not that must mean new electrons arrive frome somewhere to take their place. So Question two Where do all these electrons come from (that is how do they get to the negative terminal?) ? Question three Why is the positive terminal positive?
-
The thing is they don't have to be big and scary. I have been trying to teach leprechaun who does my washing up to write my posts for Scienceforums.
-
Perhaps these responses are a bit harsh and some humility is in order. I have been frankly amazed (along with many others) at the fantastic creatures shown on Blue Planet II by David Attenborough. Remember more people have walked on the Moon than the very bottom of the Pacific Ocean.
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
As I said, but you didn't acknowledge, when you start using words for the purpose for which they were intended, rational discussion can move forward. You have the germ of an idea which lies somewhere between the Thompson 1904 'plum pudding' model of the atom and the Bohr 1913 orbital model. Probably quite close to the Rutherford 1911 model. However, they all called Helium, Helium and Hydrogen, Hydrogen. That enabled discussion. There was a great deal of head scratching in those days to come up with these three models and the history is quite interesting and pertineent to your ideas. -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
When you get to the moon, remember to bring me back a pound of green cheese. -
Yes the excellent Khan Academy video makes no unsupportable claims and is entirely within mainstream physics. And yes it make good use of the tried and tested Huygen's Principle to do this. I have reported Dalo's two fingers to my question so I will wait for the outcome before I answer your comment Geordie.
-
In your post#2 you describe Al Khalilli's lecture, But you fail to observe what he hasn't told you about this presentation. Can you see what is missing from this screenshot?
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
I am not going to waste any more time on your redefining the wheel as a cog. I will be happy to help when you are ready to use well established words conventionally. -
I don't know if you are talking about the ill fated attempt to replace 'conventional current' with 'electron current' in electric threory. That was a really bad idea and lead to much confusion in the 1990s. The plain fact is that currents can be the flow of either positive or negative charges or both. It is difficult to say which is more common. The issue was resolved by choosing a convention many years ago, now called 'conventional current'. This was neither the right nor wrong way round, but it did allow the whole of electric theory to develop to what we have today. Whatever convention you choose you have to actually choose not one but two sign conventions and you cannot avoid the situation where some quantity seems 'the wrong way round'. Therefore there is no point changing current direction conventions and I strongly recommend you stick with conventional current. Thanks for the vote of confidence expressed about my posts.
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
The only atom with two protons is called helium. Deuterium has one proton and one neutron. This is basic chemistry that I will leave you to look up as I bid you good night. -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
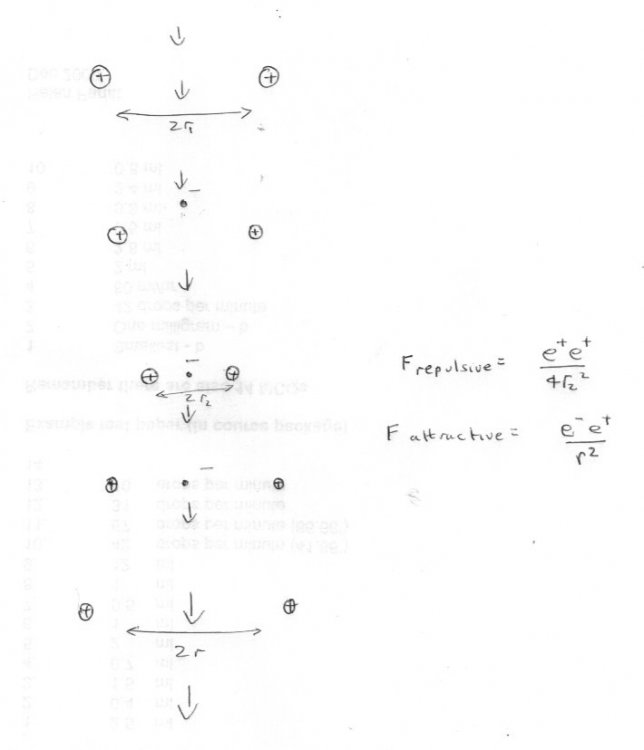
Then it is not deuterium, it is helium. So let us model helium with two protons and consider your model of the passage of one of the electrons through the gap. Classically, as you say, the electron will exert a pulling together force on both protons. At some point when it is close enough this force will be greater than the mutual repulsive force of the two positive charges, depending upon the dimensions of the gap. This effect will be greatest when the electron is centered between the two protons. After this point the effect will diminish as the electrons passes the centre. So the passage of the electron will cause the protons to oscillate closer and further in position. Have I understood your model correctly? -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
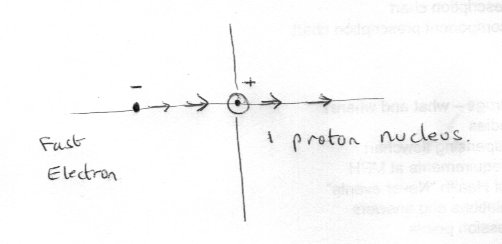
Note deuterium has only one electron. Here is my problem. Take the simplest atom, that of hydrogen with exactly one proton and one electron. You say that the electron passes through the nucleus, and the centre of the hydrogen nucleus is smack bang in the centre of its only proton. So the electron must pass clean through the proton. -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
I don't follow this. You say the protons are pulled back. Why or what do you think pulls the proton(s)? Pulled back from where to where? -
Many thanks to Butch for appearing in this timewarp photo. It clearly shows that the new software upgrade has made no inroads in fixing time paradoxes/anomalies in the forum presentation.
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
Although my question was rhetorical and addressed to swansont, thank you for attempting an answer. I would be more than interested for you to expand on the mechanics of a positive proton hurling a negative electron away as well as electrons herding protons. -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
Then why is this thread in Modern and Theoretical Physics, not Classical Physics, if we can't use all available to explain/describe something? How, for instance, do purely mechanical charged balls lead to chemical bonding? And why does a classical nucleus, with all that positive charge, not violently tear itself apart? -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
Nor is the electron a point. In fact it could be regarded as a smeared out comet like something with a dense head and a long tail that it drags through/past the nucleus. In this view the nucleus is much closer to a point than an electron in an atom. The electron could be said to gather itself together in a more pointlike fashion in an electron beam, when it is free of the atom. -
Yes we all agree this, but it should be remembered that both particles and waves are idealisations. We can use them in analysis because one characteristic or another has a dominant role, so we can ignore others. But in the real world I don't think there is an perfect example of either.
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
Are you sending them to dancing class? -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
Molecules are fine too, they work the same (at least in principle). OK so for (1) you require solutions to the Schrodinger equation. This is full on quantum mechanics. Have you seen any plots of electron densities/probabilities? These are commonly called atomic/molecular orbitals. The point about these is that they answer the age old question: Why does the orbiting electron not spiral down into the nucleus? If you look at an atomic orbital (there ae plenty of images on Google) you will notice that the probability of finding the electron at the origin is essentially zero. So this is saying that bound electron won't fall into or through the nucleus. For completeness, when an external electron approaches an atom (whether it belongs to another atom or not) it 'sees' the atom's cloud of circling electrons shielding the nucleus. Of course this cloud is negatively charged, like the electron so the approaching electron is repelled ever more strongly, the closer it gets. The equation in this case is called Lennard-Jones potential theory. Again this means that the electron will never fall into the nucleus. So we are left with firing incredibly energetic beta particles (electrons) in an atom smasher to find out what happens. Here I look forward to one of Sensei's posts. -

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
No I mean this. There are two types of electron. 1) Those that belong to the same atom/molecule as the nucleus. 2) Those that are exterior to this atom/molecule. -

Differential equation solution when RHS is abstract
studiot replied to random_soldier1337's topic in Homework Help
Since f(x) is unknown, have you thought about examining the direction field, and the orthogonal trajectories to it, to find out what form it must have? -
Well, if I turn on a light switch the light will flood out in all directions and fill up all available space. It doesn't need pushing it just goes there. In particular, no further apparatus is needed, though additional apparatus is sometimes used for particular purposes. Further it will flood through any gaps in obstructions and try to fill the space beyond. In (your) previous threads about the double slit there was a demonstration of water waves approaching and passing a double slit. They are the same. Once generated they just keep going and spreading. They are also the same in another respect. The generated wave is a plane wave and the waves emerging from the slits are circular or spherical. Finally neither the water nor the light carries a charge. But the electron does. This is fortuitous since a free electrons does not readily jump through gaps. It wanders about randomly until it is snapped up by nearby matter particles. The fact that it is charged allows us to accelerate and direct it so that we can send it through the slit. But this requires extra apparatus which is normally ignored when discussing the slits. So the electron has to be forced through. The photon just wanders through naturally. As you with me thus far?
-

If an electron falls through the nucleus of an atom...
studiot replied to Butch's topic in Speculations
What sort of electron? -
So why is it technically difficult? That is what my comments are about.