studiot

In a perfect world rotation about any of the three Euler axes is stable, an governed by three non linear coupled differential equations. [math]A\frac{{d{\omega _1}}}{{dt}} = \left( {B - C} \right){\omega _2}{\omega _3}[/math] [math]B\frac{{d{\omega _2}}}{{dt}} = \left( {C - A} \right){\omega _3}{\omega _1}[/math] [math]C\frac{{d{\omega _3}}}{{dt}} = \left( {A - B} \right){\omega _1}{\omega _2}[/math] Where constants A < B < C Because of the couping the slightest perturbation of [math]{\omega _2}[/math] will lead to regenerative instability of rotation about the intermediate axis as your vids show. The equation set can be linearised and the linearised equations set still exhibits this instability. Would you like to explain how your animations improve on this? Also the above calculations show what happens if you introduce the perturbation into either [math]{\omega _1}[/math] or [math]{\omega _3}[/math] Can you animations show this?

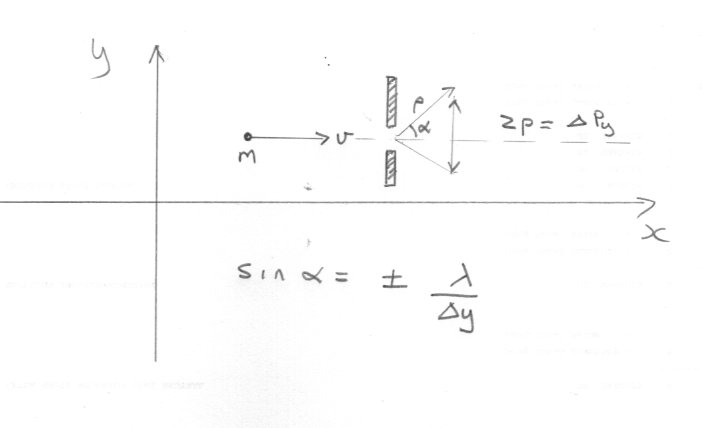
So suppose a stream of quantum particles of mass m moves along the x axis with speed v as shown. Let us try to determine the y coordinate of the particle by placing a slit of height [math]\Delta y[/math] in its path. The De Broglie wavelength, lambda, is [math]\lambda = \frac{h}{{mv}}[/math] It is an observed fact that diffraction will occur as the particles passes through the slit (this is a single slit and not the double slit experiment) causing a new direction and momentum to the aprticles, within an angular spread[math] \pm \alpha [/math] where [math]\sin \alpha = \frac{{ \pm \lambda }}{{\Delta y}}[/math] The attempt to determine the y positionof the particle has led to an uncertainty [math]\Delta {p_y}[/math] in the y componeent of the momentum. [math]\Delta {p_y} = 2p\sin \alpha [/math] Thus [math]\Delta y\Delta {p_y} = 2p\lambda [/math] or of the order of 2h However the particle may be considered anywhere within that range so it only provides the outer limits. This boils down to the greater than or equals sign [math]\Delta y\Delta {p_y} \ge \frac{h}{{4\pi }}[/math] Some years alter it was found convenient to introduce a revided version of Plank's constant and add the bar to the h. So [math]\hbar = \frac{h}{{2\pi }}[/math] In this format the HUP becomes [math]\Delta y\Delta {p_y} \ge \frac{\hbar }{2}[/math]

When I've complete my sketch in about 5 minutes, I will post a nice easy derivation, without the difficult maths. Meanwhile look again and check if your sources use an inequality. The Uncertainty Principle is not an equation.

Since neither are correct what is the book? And what are X and P ?

I'm trying very hard to be heard here, without shouting. Your plots are titled "Buildup of gravity in a sphere" Perhaps this is where your difficulty lies? I (and I believe the rest of the members responding) have been talking about gravity outside a sphere. The distribution of gravity inside that same sphere can be quite complicated. The study of gravity inside the sphere (or other shape) is known as Geodesy (Greek for the shape of the Earth) and the world standard textbook for this, which I used as my postgrad text in that subject is Geodesy by Bomford. Oxford University Press. You need to be aware that the 'sphere' reaches to its highest point - Mount Everest in the case of the Earth. The existence of the Himalaya was originally deduced by the deflection of survey plumb bobs due to increased gravity on one side. Today satellites and aircraft routinely conduct gravimetric surveys which reveal all sorts of local variations in the strength and direction of gravity and thus tell us about the underlying rocks. But these effects are all 'within the sphere'. Gauss' Law still holds

Well it can in New Zealand. https://www.theguardian.com/world/2017/mar/16/new-zealand-river-granted-same-legal-rights-as-human-being

Distribution is not the same as composition. We have an old saying in English ( a trick question) Which weighs more a pound of lead or a pound of feathers?

You can't draw power that isn't there. That's called - yes you guessed it - conservation of energy. Now please tell us why you haven't commented on the Elihu Thomson stuff swansont introduced and I gave you more about. That really is the fun part of basic electromagnetics.

The composition of the matter have no effect on gravity , I only claim that the number (amount) of protons +neutrons is proportional to gravity . This (p+n ) is the same we put on the scale every day , and only reserve I have is that speed of light stays the same for Ti . NA because mol is the only quantity with weight(known by the grams /NA (that I know ) , in this case 1kmol =kg = 1000 NA (p+n). Since kg*kg =kg2 *N2 division by 1000NA give kgNA , I divided by kg and NA have no quality . Your question on conversion factors I do not find. Timo, look carefully where you are copy/pasting from or you will be attributing quotes to the wrong person as you have done here. I didn't say that and have not been discussing composition or Avogadro with you. I came back to this thread to add something to my last post but you got here before me, so please consider this as further explanation of the attachment in my last post. No doubt you will notice the derivation uses the Normal component. This is because the normal (and outward normal at that - are you aware there are two normals?) is the only part of the flux that can pass through the enclosing surface without being balanced out by a corresponding oppositely directed contribution from another part of the enclosed mass. In other words for every component at a point on the surface perpendicular to the normal there is an equal an opposite component somewhere else on that surface. Thank you for taking notice about my comment on chemistry, did you notice I had responded in that thread?

You missed my point. The total flux through a closed surface is independent of the angle of incidence on that surface or how smooth or wrinkly that surface is. It is rather like that old theorem from Euclid that all parallelograms on the same base have the same area, no matter how skewed they are. Notice that the derivation refers to the total mass enclosed, the distribution of that mass is unimportant ouside the surface.

Gauss's Law refers to the integral of flux through a closed surface. The only directional effect is (for 3D) in or out.

Thanks for participating in the community. +1

Nor am I sure, but if you don't thinks solitons are matter, try standing in the way of the Severn Bore. I have heard of people modelling sub atomic particles and photons as solitons. There is some stuff about this is the University of Cambridge Applied Maths series books. Solitons an Introduction Drazin and Johnson, but they understandably concentrate of calculation methods. I don't have Drazin's other book to check.

Doesn't the sun shine out of your President's _ _ _ ? So perhaps you could dispense with the satellites if you placed your solar panels in the right location.

Clearly put sirs. +1

Try this https://www.google.co.uk/search?q=knot+theory+and+solitons&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&dcr=0&ei=5crrWcH8BoKh4gSm8b4I

Well you have successfully contradicted yourself. No wonder everyone is confused. I was only trying to help you employ the correct terminology that everyone else uses so they they will understand you.

Yes, there is no 'end' to put it at. But we can still handle the totality of the unending sequence mathematically (consistently), if we follow the rules. +1 John, I liked your 'proof' because it follows the same path that is used in standard derivations of sum to infinity of several standard series, although doubling is more usual than multiplying by 10.

Amplitude, with the greates respect, I don't think you have properly looked at the replies offered here. I agree that at school level few proofs are offered, which is why John Cuthber's idea was so neat. But you haven't replied to it. Yes there are many things we have to take on trust at a lower level, which then become explained as we progress in education. I have always thought it to be a sort of 'spiral process' whereby each year we look back at what we simply accepted last year in the light of the new stuff we have now learned. You are bringing in concepts from higher levels and frankly, you do not understand all of these yet so are making basic but fundamental errors. The first and worst is not listening when someone points these out. Successors, do not apply to real numbers. Integers do not have a 'number line', they are a discontinuous or discrete set of disconnected or isolated points. Real number are not and we can properly talk of a number line for them. But these are all material from more advanced (university ) mathematics. Why is it Not OK for the answer to your question to be couched in the terms of higher maths, but OK for you to introduce it in your attempts to refute a proposition?

Edit Very Important The following is correct for 1kg sized objects, but it does not apply to electron sized objects. It sounds like you are asing about what we call 'Contact Mechanics' in Materials Science and related sciences. There are Elastic formula to this problem for the stress distribution in. The original developer of these stresses was Hertz, https://www.google.co.uk/search?q=hertzian+stress&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&dcr=0&ei=FTbrWeXhAc7A8geP6JrgDg although Coulomb previously offered solutions in Geology, Soil Mechanics and foundation engineering. https://www.google.co.uk/search?client=firefox-b&dcr=0&q=Coulomb+stress&oq=Coulomb+stress&gs_l=psy-ab.3..0i7i30k1l5j0l2j0i30k1l3.102840.105177.0.105721.7.7.0.0.0.0.124.756.2j5.7.0....0...1.1.64.psy-ab..0.7.749...0i7i10i30k1.0.DzRQlnNYh8c Development of this subject can be found in books on advanced elasticity, strength of materials, or mechnicas of materials. Most of these formula can be found in Roark: Formulae for stress and strain. https://www.google.co.uk/search?client=firefox-b&dcr=0&q=roark's+formulas+for+stress+and+strain&oq=Roark&gs_l=psy-ab.1.0.0i67k1l2j0l8.181493.182626.0.184564.5.5.0.0.0.0.123.567.1j4.5.0....0...1.1.64.psy-ab..0.5.560...46j0i131k1j0i46k1.0.dBx-cyoCbEU The subject also provides elastic solutions to the problems of contact area and max/min stresses and their location. https://www.google.co.uk/search?client=firefox-b&dcr=0&q=Fracture+Mechanics&oq=Fracture+Mechanics&gs_l=psy-ab.3..0l10.118752.122435.0.124577.18.18.0.0.0.0.173.2333.0j18.18.0....0...1.1.64.psy-ab..0.18.2322...0i131k1j0i67k1.0.DQugxEgc3v4 Here is the relevant page from Roark Modern treatments also include non elastic solutions from the subject of Fracture Mechanics. https://www.google.co.uk/search?client=firefox-b&dcr=0&q=Fracture+Mechanics&oq=Fracture+Mechanics&gs_l=psy-ab.3..0l10.118752.122435.0.124577.18.18.0.0.0.0.173.2333.0j18.18.0....0...1.1.64.psy-ab..0.18.2322...0i131k1j0i67k1.0.DQugxEgc3v4

Nor have you answered my question about the conversion factors you use, despite making several references to Cavendish's experiment.

Bignose and pzkpfw, +1 for more than one good posts apiece.

Since you have qualifications and bags of experience in Chemistry, it would be nice if you would help answer one or two of the questions posed here. for the benefit of others. After all, you are benefitting from discussions in Physics. Interestingly, just an unscientific observation, but the posts in Chemistry seem to attract considerably fewr cranks than the ones in Physics. by and large the Chemistry threads are genuine.

Don't know what this was all about, (and don't really want to) but +1 for openness and honesty. Cooperation beats confrontation any day!