studiot

Magnetic focusing was traditionally used in cathode ray tubes (CRTS) for televisions, unlike CRTs for oscilloscopes which use electrostatic focusing.

I'm afraid that the Wiki article is one of the easiest I have seen, which is why I chose it. Keep at it and hopefully enough will come clear. Very quickly affine is what happens when we add a constant to linear and arises from the difference between linear and straight line. The definition of linear is that for any function f(x) multiplied by a constant af(x) = f(ax) If we add another constant to x this is not satisfied. My sketch shows this is equivalent to moving the origin to a point C Look at my diagram and try a few straight lines and sketching in the effect of y = a(mx + c) and y = m(ax) + c When we move the origin to a new point c it is an affine transformation

No there is nothing wrong with the question, it is a good one. Further I do have you intended goal as the ultimate destination (hopefully over the weekend). Topology is concerned with the next step connectedness and also the continuity of mappings. However not all are differentiable and we need to select manifolds that are differentiable. That is why topology is too wide as it includes those. I hope you liked the method of studying the simpler lower dimensions and extending both the results and differences to higher ones. Meanwhile this Wikipedia article is more accessible than most on the subject. https://en.wikipedia.org/wiki/Real_coordinate_space

What sort of doctor did you say you were? Are you pulling my leg or pulling my teeth?

Thank you for the clarification. I understand you to be saying that Since there is no current standardisation of the tumour delineation I (we?) have compared (the region? volume? described by? ) the 50% of SUVmax isosurface the 41% of SUVmax isosurface etc etc to measure the MTV. I don't see the use of threshold as quite appropriate?

Perhaps I should make it clear I have merely addressed the headline question in the thread title. That is 4 spatial dimensions. Strange has already done an admirable job of addressing Dan's subsequent ramblings about Time and pointing out that the term he should use is space-time.

Well I don't like the word 'isocontour', since that is saying the same thing twice. I suppose the choice will depend upon the purpose of the procedure. Is this for standardisation or to set a baseline for future measurements/treatments?

A long time back (ha ha ) I posted a method of marking time that does not involve a clock, in a thread about the existence/nonexistence of time. So no I have not said (I hope) that time is not observable.

A friendly well thought out response, Prometheus. +1

Nice point. +1

Was this question aimed at my post? We are working towards an answer to this in geordief's thread here Feel free to contribute.

Definitely snappier. Solution:- Replace IPB with a Dave.

This is Engineering not Physics or Chemistry?

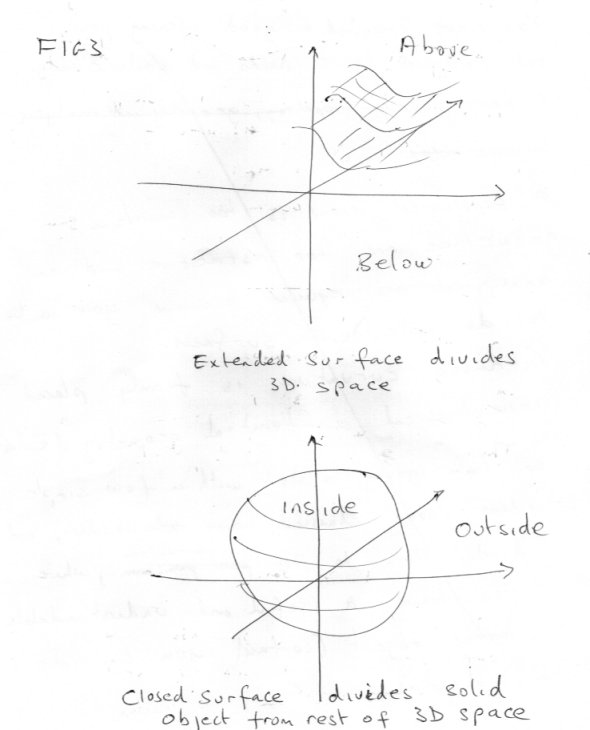
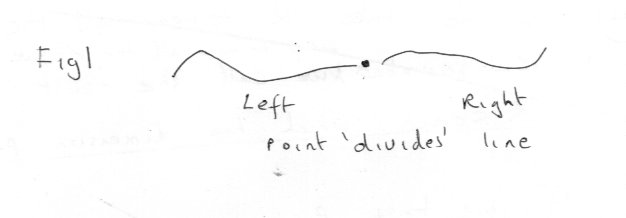
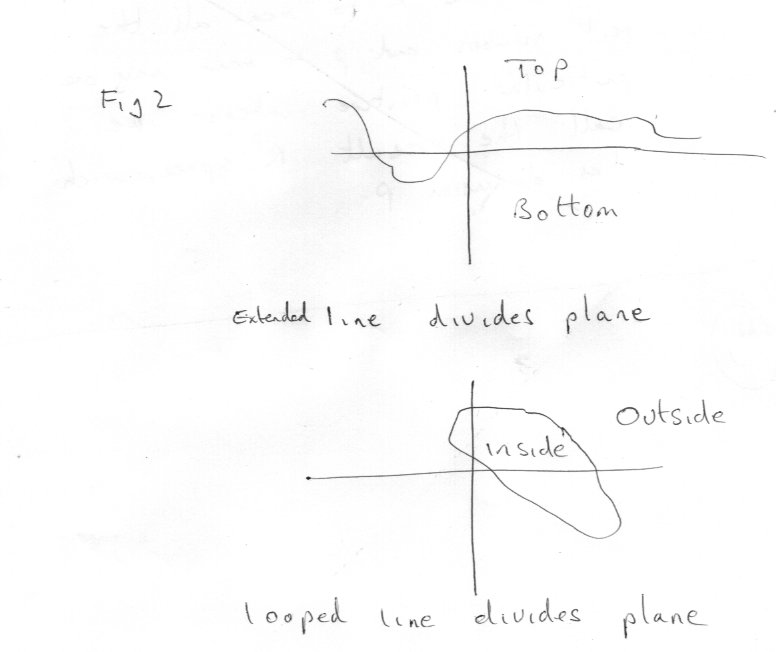
Sorry I haven’t done any significant posting for a while, but the crap new forum software doesn’t play nice with my style of posting and I’ve been too busy to cope with that recently. I’m an applied mathematician which means I concentrate on getting results and leave the burdensome task of making sure the theory is ship shape and watertight to the pure mathematicians and trust them to do that. So here’s the deal. I’m offering a unique mix of geometry, topology and mathematical analysis, blended to serve a particular purpose. After al these are branches of the same subject, not separate subjects on their own. You have presented a good opening post and explained your need and goals clearly. A topological view is too general; a geometric one to restrictive and analysis is required because you want to do calculus on surfaces. Intrinsic curvature is firmly placed in the classical differential geometry of Euler. So I am going to start with a few simple ideas, some classical, some modern, and develop them to a situation where you have a useful and understandable object (surface) you can do calculus on. Euclid said By which we mean today that 0) A point is of zero dimensions or is a 0 dimensional space. 1) A line of one dimension or is a 1 dimensional space. 2) A surface is of two dimensions or is a 2 dimensional space. 3) A solid is of three dimensions or is a 3 dimensional space. I will return to this (0) (1) (2) (3) theme a few times from different points of view., but first a theorem. If we take R to mean all the real numbers and p to mean any one particular positive integer we call the result Rp space, which has dimension p. R0 has exactly one point For any p > 0, Rp has equal numbers of points Thus Rm has the same number of points as Rn Or we can establish a one-to-one mapping between any Rm and any Rn This is the underlying reason that allows us to write down (and sometimes solve) functions and equations in Mathematical Physics and do ‘calculus' on them to find and compare properties like curvature. So 0) R0, a zero dimensional space is a point 1) R1, a one dimensional space is a line Notes A line in this sense has no ends and may be straight or curved, looped or open and extended. Parts of a line have ends and are called a line segment or just a segment. 2) R2, a two dimensional space has no boundaries, just as a one dimensional line has no ends 3) R3, a three dimensional space, is the normal everyday space we live and do Physics in and again has no boundaries. Back again to my 0,1,2,3 from a different point of view. 0) A point is indivisible. 1) A point divides a line into two parts. Note the line is considered to extend indefinitely in both directions. 2) A line divides a surface into two parts 3) A surface divides 3 dimensional space into two parts. Summary an (n-1) dimensional space divides an n dimensional space into two parts. We call an (n-1) dimensional space an (n-1) dimensional hypersurface. But can an (n-2) space divide an n dimensional space? Well a single point can’t divide a plane – you can always go around it A line can exist in 3 dimensional space, but you can always go around it. So no, spaces of lower order than (n-1) can’t divide n space and the reason why we single out (n-1) space for special treatment. This last bit introduced some new ideas, That we can embed a lower dimensional space in one of higher dimension, Or equivalently we can select a part of a space to create a complete space of lower dimension. This selection is then called a subspace. So The point in FIG1 is a zero dimensional space embedded in a one dimensional space The line in FIG2 is a one dimensional subspace embedded in a two dimensional space The surface in FIG3 is a two dimensional subspace embedded in a three dimensional space But There is also something different between FIGs 2 and 3 and FIG 1. FIG2 contains a looped line as well as an extended one and FIG3 a closed surface, as well as an extended one. This brings us to the topological definition of a surface. “A surface is a two dimensional boundary between a solid object in a 3 dimensional space” As this is a work in progress We shall see in the next instalment that this is too general for our purposes, and find out that what we need to retain from topology is connectness and compactness to enable continuity and therefore calculus We will also revisit the 0,1,2,3 again to introduce parameters.

A word about your technique. Please don't react the wrong way to this, it is meant to help you progress whatever your goal actually is. The most important thing to learn here would be to stop using terms and notation that already have very well and tightly defined meanings for something entirely different. I'm sure the moderators do not expect this when they said Such presentation makes your posts impenetrable to even the most intelligent members and leads to comments like this So start with your basic object and give it a name. It is not a number so how about duplet or couplet since it appears to be formed of two simpler objects joined together in some way. Then you can explain how the joining process works and what you can do with your object. If you must use the term 'binary expression' (which establishes a connection between two objects) you (and others) will then be in a position to distinguish between your object (see why it needs a name of its own?) and objects already named and defined by you or anybody else. I really hope this helps you progress.

I have been unsure as to your position on the topic, since your comments have all been rather cryptic. But thinking about it, you are right that at many discontinuities some physical, measurable quantity has multiple values (the imperfection of our equipment aside). The hydraulic jump is one such which has a discontinuity with duplicate values in the specific energy line. Other examples would be the electrical output v time of a square wave generator or a staircase generator.

So can you show this for the mathematics of the hydraulic jump since that was one of my OP examples?

Who said anything about Physics? Did you read the thread title or the OP? Here is an example from mathematics that is as clear cut as I can make it The integer line is discontinuous The real number line is continuous But I don't see any multiple values in either.

Yeah, I like it.

Stating there Surely that is a contradiction, (hence Bell's paradox) not a discontinuity ?

Let me try to cool this discussion off a bit. Cladking, can you tell us the purpose of the thermal imaging and the timescale over which it was conducted? I ask because one of the projects I was once associated with occurred when the builders of two 400+ metre bridge girders made them over 120mm too short. The solution involved measuring the thermal profile of that bridge, which was a very tricky operation.

Thank you for replying, but I don't see a discontinuity. Can you pinpoint it ? The endpoint of a load extension graph is not a discontinuity since the graph does not go beyond that point.

Have you lost interest here?

Yes, http://scienceworld.wolfram.com/physics/SpeedofLight.html

Hello geordie, Yes there is more than one definition of a surface in Mathematics, and yes they exist in high dimensions and are called hypersurfaces. To best understand this start with 2 dimensions. A surface is a two dimensional plot or graph in three dimensions, of the function z = f(x,y) or f(x,y,z) = 0 Another definition is that a surface is a connected set of locally flat points. Such a set can be a subset or subspace of any number of higher dimensions, but is still a two dimensional manifold. I will draw some (hopefully helpful) diagrams when I have time.