studiot

This maths starts with an elementary mistake. The forces are not balanced yet the author writes an equilibrium equation as though the ball and wheel were in equilibrium. They cannot be in equilibrium since they are in motion, suffering accelerations and decelerations. So can we have a correct analysis please?

A video from 1823?

Not quite I think. Check the geometry very carfully for the position of the centre of gravity.

Maybe it is your English, but you made a statement about Newtonian mechanics that was only partly true. Perhaps you should try to improve your English, then your Newtonian Mechanics before doing any more relativity? I thjought you might like to try the Newtonian puzzle I posted in the puzzles section (about Alice) The result is quite suprising.

Force = time rate of change of momentum. But Newton's first Law also considers the situation where there is motion, but no force. Where there is motion, but no force, there is still momentum. There is just no change of momentum.

Be aware that the previous Ransomwares later versions (cryptolocker type) could access cloud remotely stored data, on your server or the cloud. This would be locked as well.

Or sometimes not, as dictated by Newton's First Law.

And I'm sure that same motor will be much more difficult to start after standing still for 5 years in adverse weather conditions, poor starting due to seizing of bearings etc. Motors run in journals, lubricated or self lubricated. These are designed to be self optimising under running conditions, but gravity etc will redistribute the lubricant I see no difficulty with a short period after stopping where the bearing remains close to the optimum.

The way to teat momentum, velocity, etc relativistically is to use the 4D versions That is use 4-momentum, 4-velocity and so on. These physical quantities are much better behaved, just as you would be with two arms and two legs, rather than one chopped off. If you must use 3-velocity then you have been told several times now that there are no two velocities v and v' that add to c. The process of addition (or subtraction) is not one of simple adding two plain numbers together.

As always, Wiki is not quite up to high school maths The value of gravity at distance a = (R - d) from the centre is [math]g' = g\frac{a}{R}[/math] Where R is the radius of the Earth, a is the distance from the centre, g is the usual surface acceleration and d is the depth. edited to improve formula.

But why would you and how is that germane to the OP? I have already said I thought you did pretty well on your first post#2.

Hint I posted this partly because we have had lots of arguments about clocks lately and this forms an unusual clock I wondered if our resident Dr Clock had heard of.

We have all seen the news of the recent cyberattacks. I would just like to remind members of the urgent need for keeping their data backups bang up to date. These attacks can reach individuals as well as large organisations.

Pity you are getting closer.

A little mechanical analysis (you only need high school mechanics for this) will answer these side questions en route to the answer to the original question.

1) 42.5 minutes actually, Douglas Adams got it slightly wrong. 2) That is the question of the puzzle.

Sorry I didn't explain it very well but now you also make me feel ashamed as your picture is sooo much better than mine. Interestingly the answer is the same as the key question in the Hitchikers Guide to the Galaxy.

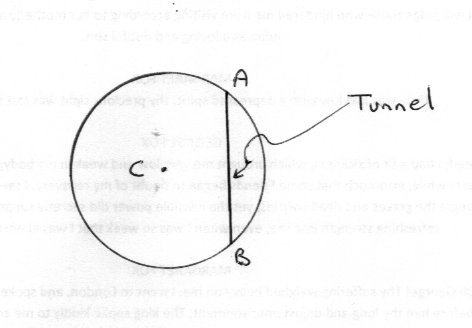
This one is a version of a problem due to Lewis Carrol, hence the thread title. A and B are two points on the surface of the Earth which are connected by a straight tunnel. Both A and B are on the same side of the centre of the Earth. Alice rolls a ball into the tunnel at A. How long will it take the ball to reach B, neglecting frictional resistances? Take the radius of the Earth as 4000miles and g = 32 ft/sc2

Since I don't know who you are or where you are or what level this is how about Temporary or permanent road construction on unstable (soft or inadequate) ground eg a bog? This should be applicable the world over.

I think itoero has deduced the link to the nature v nurture argument and presented it very well. +1 Because of this argument we just don't know is the short answer. Certainly, even in a finite universe, there is room for theoretical replication eg the roots of the equation x2 + 4x + 4 = 0.

OK, I'm glad you understand limits and that you have found Paul's Maths Pages. Paul's Pages are to be recommended. The page you link to is all about manipulation of limits as algebraic entities and a pretty comprehensive list of possible aglebraic operations on one, two or more limits and some constants. You should note something he says at the top of his excellent table. The important bit is 'assume the limits exist'. So here he sets out the conditions when the statements are true. This is very important and often forgotten in applications. It is up to the user to make sure that the usage is suitable for the application. So yes, they are true, subject to that restriction. Two important things you should remember from your understanding of limits. Firstly the fact that a limit of a fucntion at x=a exists does not mean that the function has this value at x=a. Secondly discontinuous functions may have different limits 'from the left' and 'from the right', depending upon which direction you approach the set point.

You say you are not a maths student and I'm sure uncool can put you right on the maths. But I am a little concerned by the phrase I'm looking for some identities regarding the 'tends to' part of the limit. A limit is a process and the result of that process. You need both parts of the definition to understand limits. This is simlar to the comment that a function is a process and the result of that process and also includes the 'working material' of the function, called the domain. Hilbert spaces are rather esoteric and advanced for someone who is not a maths student, if you would like to explain you interest it would help couch replies in suitable language.

Actually corner reflectors are used, not mirrors, if you want strong reflections.

Well yes and no. The Abel-Ruffini theorem refers to polynomials; these are a type of linear equations in linear algebra. In the same way a fourth or nth order linear differential equation can be written in a (linear) polynomial in the D operator eg (aD4 + bD3 + cD2 + dD + e)(x) = 0 : a, b c, d, e are constants; D is the D operator. Has a general solution related to the solution of the fourth order polynomial. Here are lots of pdfs and youtubes on solving linear differential equations by the D operator. https://www.google.co.uk/?gws_rd=ssl#q=operator+method+for+linear+differential+equations But general fourth order differential equations may contain terms that preclude this or may be nonlinear in which case the answer is no.

We used to have two phrases Common sense and Engineering commonsense. and Economics and Engineering economics. Both of these suffer from the same difference.