-
Posts
18483 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
Steiner is very good and very clear to help you with the maths you need rather than the detail the mathematicains want you to know. Takes a student through advanced high school maths and chemists through at least two years of chemistry maths at university. General Chemistry - Petrucci Chemistry - Lewis and Evans Both excellent modern reading at your level, both cover all branches of the subject at introductory level Organic, Inorganic, Analytical, environmental and radiochemistry. A fun book is Molecules - Atkins Go well in your studies and come back here with any questions, there are some good to great chemists on this site.
-
No, as imatfaal says you can't just add the percentages. You need to create a new population with either stomach or a liver complaint, by adding the individual populations of each, just as you have done above. A small correction to the wording here. Hence Total % change in stomach and liver patients within a year is: should be Hence Total % change in stomach or liver patients within a year is: Further you have to make the assumption that none of the 300 stomach aptients are also counted in the 200 liver patients. Otherwise you do not have enough information. That is no patient has both a stomach and a liver complaint.
-

Why do cathode ray tubes have to contain a gas at LOW PRESSURE?
studiot replied to mahela007's topic in Classical Physics
Of course the interesting thing is that before the PC came along (monochrome version) we had the Compucolor II with graphics, inbuilt drive, and an inbuilt cathode ray tube that was a pig to align properly oh and I nearly forgot , virus immunity. That was built on an 8080 processor. -

Why do cathode ray tubes have to contain a gas at LOW PRESSURE?
studiot replied to mahela007's topic in Classical Physics
Lol indeed You youngsters have it so easy these days. When I did my thesis ( A complete hydrographic survey of Plymouth Sound), just after this thread was started, The most common computer commetn was !Runtime Error.in line 35 We did our computing by manually puching a set of cards, putting an elastic band arond them an puttinf them into the 'in' wire basket in the computer dept hatch. Some days later (next day if we were very lucky) the cards would beappear in the 'out', folded in the output printout on that famous 'music paper.. It took me a smester to design and program a least squares analysis of the survey control net. -
Don't you think both methods of assessment have their place, along with others that you haven't mentioned? Why does it have to be one or the other in an all or nothing manner? I couldn't make head nor tail of your last paragraph, perhaps because it was so wan besides the bright lights of the first four. Could you please explain what you are trying to say?
-
Einstein's field equations have been found to have many different solutions. Just to increase the complications the equations themselves developed and changed over half a century. Here is an extract from Eddington : The Mathematical Theory of Relativity that contrasts a solution by De Sitter with Einstein's own. Note the paragraph under the equations that considers rest and motion. A later more bizarre solution was due to Godel (1949) This one allows time travel. The equations themselves are non-linear, so it is not necessarily so that combinations of solutions are also solutions, though this possibility is not ruled out either.
-
You can be a Dr. with or without a Ph.D. simply by being a medical doctor, anywhere.
-

Why do cathode ray tubes have to contain a gas at LOW PRESSURE?
studiot replied to mahela007's topic in Classical Physics
Didn't cathode ray tubes go out of date shortly after 2009? -
You know you are completely right about one thing and it was a very good question. The model proposed by MigL does indeed require motion in order to develop an apparent force and offers no answer as to why there might be one between objects with zero relative motion. Interestingly Einstein in his paper submitted in 1915 to the Prussian academy says at greater length than this shortened translation: "What we perceive as gravity is nothing more than objects moving in the geometry of spacetime" I was rather concentrating on the geometry of spacetime part, which is in some ways much easier for me. It is good to have separated this into two questions, one about motion and the other about geometry. I am therefore searching for a model to demonstrate the attraction. I would be grateful for help from anyone who knows more about the Einstein Field Eqautions than I do (not difficult). Perhaps MigL has another, better model up his sleeve cigar?
-

possibility to send a message to Future?
studiot replied to Roger Dynamic Motion's topic in Speculations
This message post can only be read in the future. -
What, no technical questions at all? Well I will ask one then. Under what conditions is angular momentum conserved for a particle proceeding along a straight line as shown in post#99? There is enough information in post#99 to fully answer this. However it is only true in 2 dimensions. So a second question Why is it not true then in a general 3 dimensional case?
-
This is off topic here so I shall not refer to it again, just refer you to this article in Poinsot's Theorem and Wrenches in Mechanics. If you wish to pursue the difference between 2D and 3D please start another thread where it can be discussed at leisure. http://www.cs.cmu.edu/afs/cs/academic/class/16741-s07/www/lecture14.pdf Yet other French Mathematicians associated with differences between 2D and 3D are Varignon and Poincarre. You have already accepted movement is available in the OP. I know of nothing in General Relativity to suggest that movement is necessary to establish the apparent force of gravity. If there is I would be very grateful if you would point it out.
-
Now that we have agreed the conditions which the OP set, we can move on to the question he actually asked, and MigL offered an analogy in a simplified situation. The question that was asked boils down to Why do objects subject to gravity experience an apparent force if gravity is due to (some form of) curvature? Well Migl offered a situation where objects would indeed experience an apparent attractive force, although none really exists, due to the curvature of the 2D manifold and not due to any gravity. You come from the land of imaginary forces (D'Alambert) so you should not be so suprised at this. As to your last line, we are discussing the classical mechanics of angular momentum in another thread here and are approaching the point we we can deduce that even the simplest multidimensional system (3D) have properties that do not exist in 2D, so perhaps you would like to reconsider or rephrase this?
-
Actually he doesn't say anything of the sort, however since I know that neither you nor he have English as a first language I will explain a best I can. He actually said He did not say the system was at rest, just that any motion of the large mass is follwed by a comparable motion of the small one. One of the tenets of Relativity is that there is no such thing as absolute rest. I'm quite sure MigL can answer for himself but just remember he was trying to reduce an extremely difficult problem (visualisation in 4 dimensions) to a simpler one to promote understanding. Yes his model is not perfect, but it is very clear.
-
Welcome to Science Forums. You should definitely start by reading this here. http://www.scienceforums.net/topic/75772-read-this-before-posting-in-homework-help/ and then following the instructions. What have you done so far towards the problem?
-
Avoid marble or concrete (I think you call it cement). They are not acid resistant. Natural stone can't usually be finished to a sufficiently fine surface. Artificial stone is usually fabulously expensive, but can be effective as others have said. Epoxy or polyester resin with ground silica / mica / corundum filler. Corian is very good and relatively lightweight. A cheap alternative for the home might be resin faced shuttering ply, which is pretty hardwearing.
-
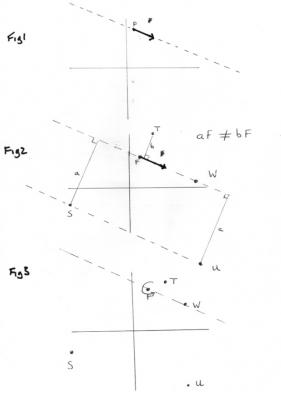
To move on to angular momentum and examine the question ‘what is angular momentum?’ I am going to go back to statics and my post#64 So consider a general force vector as in Fig 1. Like all vectors, F acts only along straight lines, shown dashed in the figure. F is both the force and its point of application. Introduce some general points, S, T, U and W in Fig 2. The moment of F about a general point is defined as the product of the perpendicular distance from the line of action to the point, as shown. Note that there does not have to be any physical object at any of these points. If there is a physical connection between F and the point (say S) about which the moment is taken then that moment is applied at S. Otherwise the moment is notional, but still exists mathematically. Fig 2 also shows some particular points. 1. The magnitude of the moment is, in general, different for every point. So the inequality shows that the moment about S is numerically different from the moment about T 2. The direction of the moment is clockwise or anticlockwise depends upon which side of the line the point lies. 3. The moment at U has the same magnitude and direction as the moment at S and U lies on a line parallel to F. So moments are only the same if they lie on a line parallel to the line of action of F 4. The moment at W is zero or does not exist and W lies on the line of action of F. Fig 3 shows that if, instead of a force we apply a couple at F we find that 1. The couple exerts the same turning effect about every point (including S, T, W and U). 2. The couple has the same direction about every point. 3. There are no points with zero moment. Quite different from the turning effect (moment) of a single force, as promised. I will not prove these unless you specifically ask, although it is an easy proof to demonstrate. A real world physics demonstration of this can be had by loosely nailing a plywood lamina to a post and comparing the turning effects of a single force via a spring balance with the turning effect of a large screwdriver, both applied at various points. A further important difference is that a single force acts asymmetrically, a couple can only be realised by a pair of forces or multiple pairs of forces, which then act symmetrically. The ultimate being an infinite number of pairs or a ring force as found in a rope round a capstan or windlass. I have mentioned symmetry because it connects directly with Noether’s theorem that Mordred referred to. Noether was a very theoretical Mathematician and it is pleasing that her theorem (1918) manifests itself in physical reality but there is no reason to expect physical reality to follow modern theoretical mathematics. There is plenty of such modern mathematics that has no physical counterpart. Earlier Mathematics was structured to follow physical reality. Force is a vector and if we now replace this vector with another one, either velocity or linear momentum we find what is known as ‘moment of momentum’. This is an instantaneous quantity and the point it is taken about is called the instantaneous centre. For a general motion this will change with the motion of the body at F. It is unsymmetrical, like the moment described above and in the same way that the moment changes, the moment of momentum changes. But I mentioned two modes of turning motion and the second is called spin. This corresponds to the couple in statics and is a symmetrical mode. A spinning body possesses angular momentum S, by virtue of its spin as well as moment of momentum by virtue of its translational motion. Its total angular momentum is then the (vector) sum of these. Hence my previous comment that there is an extra term in the equation. We can explore a simplified version of this in the next instalment and find out the conditions that lead to conservation of total angular momentum and also the complete muddle that modern presentations have got themselves into. We can also explore why adding couples and the moments of forces in the first part is simpler and easier that adding moment of momentum and spin. Now that we are on better speaking terms I'm sure there must be questions, don't hesitate to ask.
-
Thanks Moontanman, I've not seen the first one before. Don't forget that this sort of effect has been put to good use in things like the impellers driving sealed pumps. +1
- 1 reply
-
1
-
No. In the first place the radiation of an EM filed is a classic wave effect, and only occurs when the charge is accelerating. In the second place the emission of a photon is a quantum effect and in this case there is no emission dues to acceleration. For instance the electron does not spiral into the nucleus, loosing energy by emitting photons. The emission of EM waves is typified by the X rays emitted by a cathode ray stream, accelerated in a vacuum tube. The re is obviously a relationship between the X rays and the elctron stream, but it is not quantised. Here is a nice gif of the emission of EM by a moving charge, courtesy NASA.
-
But maglev requires a dedicated track. That is the whole point. No one system is perfect and the best one deopends upon a tradeoff of benefits and disbenefits.
-
Both your statement "where it was before" and Eise's It will deviate from the time axis imply an absolute axis. In Eise's case the phrase 'the time axis' In your case where 'it was before' give the game away. Ignoring the fact that you cannot simply 'add a mass' think of it this way There are two different situations being compared and measurements in one system cannot be subtracted from measurements in the other to say 'it moved'. The system with one mass has a different coordinate system from the system with two masses, they can never be the same. There will be a third system to which you can reduce both the original scenarios, and in which you can say 'it moved' But then again there will be many others in which 'it moved differently' is appropriately and finally possibly one in which 'it did not move at all' All these systems are equally valid, that is the point of relativity. Gauss' Theorema Egrerium says that the measure of the projection of the comparison is invariant in all manifolds.
-
Once again this analogy is fatally flawed as is implies there is some absolute reference underlying both the gridlines and the object's 'true ' position. There is no absolute reference to say that 'it moved'.