studiot

Do you think this also applies to non-conservative fields, sources or sinks? How do you describe the situation if I introduce an object eg a piece of wood or plastic into a magnetic or electric field?

No detection is not a prerequisite. No he gave a mathematical explanation (but see below) so they are mathematical objects ie objects recognised by mathematics. Yes they can be potential objects - the most famous would be potential energy - and a PE field could conform to your if question, but it doesn't have to. I think this definition is a tad too wide since all the 'objects' of the field must be of the same type. OK so here is my take. A field as defined in mathematics is not quite the same as a field as defined in physics. Since this is a Physics question here is a Physics answer. A field has (at least) two parts. The field variable, which may, as Srinam says be a Force or it may be quite another quantity. The type or name of the field is usually named after the field variable so we have magnetic fields, velocity fields, temperature fields and so on. The field is just a catalog of the values of the field variable in some region of space at a particular point in time. It may be a static field in which case the values do not change with time or it may be a dynamic field in which case the values change with time. The values in a constant field do not change with position in the region. This is important for vector fields. The coordinate system of position in the region is separate from the coordinate system describing the values of the field variable. Note I said the field variable may have more than one value. Field variables with only one value at any point are called scalars and their own coordinate system is called a scale. All the values of a field variable in a scalar field must have be of the same type eg evrey value in a temperature field must be a temperature. Field variables with more than one value may be called vectors or tensors depending upon the number of type of the values. If a field variable has more than one value the different values need not be of the same type eg a vector field variable has two values, magnitude and direction which are different types of quantity.

Unfortunately I get error 404 when I try your latest link. I assume that link was to somewhere that defines the factorisation of infinity? Here is a good discussion about the properties of infinity, including good background on the issues from my post#29 you keep avoiding. https://www.quora.com/What-is-infinity-raised-to-the-power-infinity I note you are also avoiding the difficult bits of my post#38 as well.

Well said Xerxes. +1 SFNrtc, I recommend drawing diagrams to help understand Xerxes comments.

One thing to be careful of is the way the metric system handles the relationship between mass and force. There are two units called the kilogramme. Kilogramme of mass Kilogramme of Force - this is not used much and not part of Systeme Internationale (SI). Remembering that weight is a force and using the previous two posts we have 1 kilogramme (mass) weighs 1 x 10 = 10 Newtons ie the force of gravity on 1 kg is 10N. 10 is a good enough factor for most things but use 9.81 if you prefer. This is a reversal of the situation with imperial units where pounds usually refers to pounds force or pounds weight, not pounds mass. Pounds, mass gives a force in poundals.

Nice to see folks cooperatively working through the possibilities with open minds. +1Acme and Mman

I'm sorry, where was factorisation of an infinity defined either in your mathpages link or in the Wikipedia reference from wtf? I note you haven't addressed my post#29 about mathpages

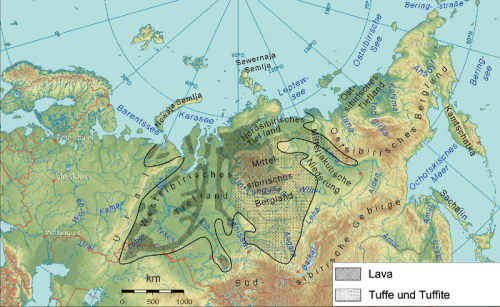
If you read the translated russian pdf I linked to it tells us that the lava flows were basaltic, not granitic

Well go ahead and do the evaluation please. As written you run straight into the issue that [math]\infty - \infty [/math] is undefined. If you manipulate the expression algebraically to avoid this, you run into the issue that you have to use different rules of algebra for [math]n = \infty [/math] and for [math]n \ne \infty [/math] This is OK if you can guarantee that n is one or the other, but what if you don't know? Here is a more difficult example, where ill considered manipulation can get you into a great deal of trouble. Consider the sum to infinity of the following two series similar to those before. [math]{S_c} = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}}.....[/math] [math]2{S_c} = 2 + 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{{16}} + \frac{1}{{32}}.... = 2 + {S_c}[/math] Which implies [math]{S_c} = 2[/math] since [math]2{S_c} - {S_c} = 2[/math] But if you try to substitute infinity for Sc and 2Sc you get [math]\infty - \infty [/math] Worse, trying this manipulation with [math]{S_d} = 1 + 2 + 4 + 8 + 16 + 32.......[/math] leads to [math]{S_d} = - 1[/math] Of course the former series is convergent and the latter divergent. You cannot treat the results of the limiting process the same on a convergent and divergent series etc.

It's the old story of the Teacher coming into the playground and saying "I don't care who started the fight, but I'm finishing it" I gave phi +1 for doing this before it got out of hand.

Well the definition of range sounds like what you are describing since it defines 'how far you can go'. It comes from the oldest stats book I have Statistical Methods by F.C Mills, Professor of Economics and Statistics at Columbia. (1924)

Some expansion of this would help understand what you are referring to?

Only 10 years? Perhaps your memory has slipped? There was a time when they used to distinguish between 'absolute variation' and 'relative variation' Perhaps you are referring to this? Relative variation is the fore runner of the modern approach. Absolute variation was renamed to range about 1920.

I see no point discussing further, considering your response to myself and others when we try to help.

Of course there is but you need to distinguish between expressions, formulae, equations, identities, variables etc. For instance the general quadratic equation in two variables is Ax2 + Bx + Cxy+ Dy2 + Ey + F = 0 You should write your expressions in this form for as many variables as you have.

I have found some useful further information but need help posting to comply with the wikimedia licence attributing the sources. Please help. http://www.mantleplumes.org/WebpagePDFs/Siberia.pdf https://commons.wikimedia.org/wiki/File:Extent_of_Siberian_traps_german.png https://commons.wikimedia.org/wiki/File:Extent_of_Siberian_traps_german.png#/media/File:Extent_of_Siberian_traps-ru.svg

Hey fellas, I count two questions marks in the OP which makes two questions. So both are right in the question they choose to answer, if they are only going to address one. And both are wrong if they dismiss the other question.

Note Swansont also said entropy can remain the same. That is not the same as entropy increases unconditionally with time.

According to my admittedly coarse scale geology map, this area of the Central Siberian Plateau is a tongue of Qaternery material extending from a much larger area comprising the Yenisei-Irtysh basins., to the west. This is shown in yellow on the map. This tongue is sandwiched between much older formations to the north and south, first Palaeozoic rocks shown blue and purple followed by some Pre-Cambrian, shown brown. This is suggestive of a former syncline. (Youngest rocks in the middle) on a much larger scale than the 10km feature in the OP. http://web.arc.losrios.edu/~borougt/GeologicStructuresDiagrams.htm The rivers run through the Quaternary material, which must be softer than the older rocks and Imatfaal has show to be lower. Not only lower but the Google pictures show that the rivers have cut quite deeply into the plains with the older rocks forming background peaks. The Google maps also show much meandering, typical of low gradients. https://www.google.co.uk/search?q=river+kotuy&biw=1366&bih=679&source=lnms&tbm=isch&sa=X&ved=0ahUKEwiA89Sfn-LRAhUkLMAKHf09DigQ_AUICCgD The point about the ages is that known igneous activity preceded the Quaternary deposition, so the feature in question may be a remnant intrusive dome the radial lines could be old dykes, although the river seems to have cut straight through one (perhaps following an earlier glaciation). I bet there are some lovely rapids there.

A screenshot would be useful to those of us without your special equipment.

No Please read my post#20 very carefully. I am not saying you are right or wrong nor am I proposing alternatives. I am examining it for logical self consistency and consequences. I think this is a good thing to do because there is a danger of 'running away with oneself' when proposing a hypothesis. You have made contradictory statements that the particle and wave are at the same point at the same time and that the wave arrives before the particle. Please clarify this as they cannot both be right. Incidentally your description of wave-particle sounds something like the wavelet or wavicle models. Incidentally it is a mistake to fall into the trap of thinking that light has to be either a wave or a particle. It has some characteristics (but not all) of each, but is actually more complicated than either. Another example of such a physical phenomenon is that of (ordinary) glass. Glass has some characteristics of a solid and some of a liquid but not all of either and is in fact more complicated than either.

My thanks to both wtf and Nedcim for holding an adult discussion about this subject. +1 NedCim, your mathpage link was vastly superior to your previous one and offers some very well presented examples. I note they said exactly what I did That a limit is a number and infinity is not a number. and [math]\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \tan x[/math] does not exist They do offer something of an explanation but Oh dear. Firstly they say that when we say some limit = infinity we mean something other than conventional 'equals' and the reader needs to know the new conventions. Better, I say, to avoid such confusion. They then compound the confusion by introducing two different 'infinities'. (via Gauss' reference to the potential and actual infinities of Archimedes and Eudoxus) Whoops, what's that ? We are only allowed one in the extended real number system. We do not have any rules for two types of infinity. They also discuss something 'becoming infinite or infinity' What's that? Do the rules suddenly change when this happens and what are the rules to know how, if and when it occurs? In particular if you are going to do some algebra on my question you need to prove which set of rules the n's involved obey and when since n 'becomes infinity' in the limiting process. Finally they make the classic mistake of claiming that we never reach a limit. This cannot be true since the definition of continuity at some point, xo requires that the value of a function equals its limit at xo. So to say we can never reach a limit (or that the limit is never included in the set) is stating that we can never reach, say the value of f(x) = x2, a x=2. Sorry I didn't make my last explanation very clear. I will post some background starting from what my sources say was the first formal definition of a limit (Wallis : Arithmetica Infinitorum 1655) going right up to the material you say is hard to find ( Thurston has some vary good pages similar to your Wikipedia article, but without the gloss over the difficult or missing bits)

Not sure why you are replying to me, Mike? I don't recall ever discussing grad, div & curl with you.

Thank you for replying to my question. Do you then agree that the particles arrive after the waves in your hypothesis, not simultaneously as you originally stated? How does this affect your hypothesis?

Isn't referring to 'fluid dynamics' a bit limiting? How about Continuum Mechanics which includes FD and much more besides? I say this because there are many texts at many levels including this in the title.