-
Posts
18483 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
http://www.bbc.co.uk/news/health-39518580 This seems to be a highly significant breakthrough, if verified. Further references welcome.
-
Strange, see my post#10 ref
-
I posted a comments on the twins in this recent thread, now closed. No one seems to have taken up on as a way of avoiding the acceleration question. I don't know if I may refer directly to the thread but the post was #109.
-
Do you really mean 'infinity' or perhaps 'somehow all inclusive or all exclusive within the context of the proposition' Rule1) There are no rules. Buy Johnston's biodegradable, indestructible socks. A self-effacing process.
-
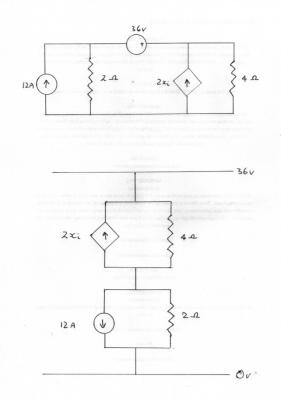
This whole question is rather puzzling. It is puzzling because the material is not taught until a specialised course in electronic engineering at University or College. It is not even always taught in similar level electrical engineering course. Previously you struggled with some much simpler problems that might have been offered in Physics at A level in secondary education. You have said that you are preparing for imminent exams, so what are you studying? We want to help but it would be really useful to know where you are coming from. Back to the question. You have a circuit with 5 elements, three of which do not obey Ohm's law and two of which do. In the circles you have a fixed current source of 12A and a fixed voltage source of 36V. You seem to have added 12 amps to 36 volts at some stage in your figuring? In the diamond you have a current controlled current source of value 2xi where xi is a circuit variable from somewhere else in the circuit. Unfortunately you have not told us what the question says about xi There are 6 loops in the arrangement, but not all of them represent independent equations. I have said to you before you should redraw a circuit into the most convenient form (teachers like to obfuscate to exercise the mind) and that you should get used to recognising small series and parallel arrangements. I have done this below, the second diagram shows your circuit in standard form. Note the current sources are working in opposing directions.
-
Well yes I did find some pills but I can't remember what I'm supposed to do with them, perhaps a glass of your instant water might be useful. Don't worry about the debt, phi, I've just made an amazing discovery - negative numbers. I will pay you -1000% interest so If I could just remember my bank account number I could tell you where to pay it in.
-

How does a body "know" how to move??!!
studiot replied to Rasher Null's topic in Modern and Theoretical Physics
I can't for the life of me see how what I said could have given you that impression, but I am sorry if it misled you. Read inertial frame for coordinate system if you will. Personally I don't like the term (inertial) frame as it means something quite different to me, but it is well used. -
Oh drat I remember now it was the memory pills I was looking for.
-
When you have helped JC (+1) perhaps you can help find that £50,000 note I lost last week.
-

How does a body "know" how to move??!!
studiot replied to Rasher Null's topic in Modern and Theoretical Physics
Points are observer dependent, ie they depend on the coordinate system. Events are agreed by all eg the twins meet again or they don't. But different observers will differ as to the point at which this happens just as with my cigar example the observers differ as to the point when the cigar burns out. Another 'point' about points and events. We are treating all bodies as 'point particles' when discussing events concerning them. This may or may not be appropriate, just as in classical mechanics. @steveupson. I introduced a particular example to answer someone else's question about whether we can observe length or time contraction or not, not to discuss your pet direction obsession. -
There is still something missing. You say 2ix is defined in the problem as I suspected, but you haven't told us what it is. I did ask for more explanation. A tip about the node Law. At least one of the currents at any node must be of opposite direction to the others, unless they are all zero. The sign that comes out of solving the equations tells you whether you have guessed the direction correctly or not.
-

How does a body "know" how to move??!!
studiot replied to Rasher Null's topic in Modern and Theoretical Physics
Now we have a response from someone who actually knows what they are talking about. Steve you should listen to ZZtop. The purpose of the ruler was to avoid the complication of a 3D object such as a cube and all the arguments that will ensue. The planet observer will not view the cube as a cube, only the rocket observer will do this. The ruler will appear to to the planet observer to grow in length when the rocker observer turns it vertical or horizontal but perpendicular to the direction of motion. Thus the planet observer will be able to witness the effect of length contraction. Because lengths perpendicular to the motion are not contracted but those parallel are directions are affected in a measurable or calculable way. -

How does a body "know" how to move??!!
studiot replied to Rasher Null's topic in Modern and Theoretical Physics
Three replies (I think) to my post#126 so far. One poster realised that length contraction alone can give direction information. One poster was realised that something would happen on turning the ruler from parallel to the direction of motion to being perpendicular to it, but was unsure what. (The guess was incorrect) One poster completely missed the point that my post was a response to the issue of difficulty in observing length contraction. No it was not a trick question. -
I don't understand your labeling in the diagram. You have written 2ix in blue against the controlled current source, which suggests it is defined in the problem. But you have written ix in red as though it was your naming of the branch currents at the nodes. Please explain.
-

How does a body "know" how to move??!!
studiot replied to Rasher Null's topic in Modern and Theoretical Physics
An interesting propositional experiment is as follows: A planet bound observer watches an astronaut approach and fly past in a spaceship at 0.8c relative velocity. The astronaut is holding straight out in front of her a 6 foot ruler, marked in feet. What will the planet observer see? Will he see all 6 foot markings? How long will he think the ruler is? If the astronaut rotates the ruler through a right angle as she passes What will the planet observer see happen to the ruler? -
Since you now deny your own words, there is nothing more to be said. Perhaps you would like to posit a relationship between space and time, consistent with your claimed properties. Meanwhile Strange +1 for an excellent set of nits.
-
So you now partially agree with my comment, in the first part of your reply. Progress. But are you asserting that space alone somehow incorporates the time property of 'the present' ? Does it also therefore incorporate the property of that which is not 'the present' ? Or are you saying there was no space in the past and there will be no space in the future? Your overshort assertions need more detailed explanation. Finally please stop the insults and discuss the subject.
-
The diagram size was fine for its purpose. You are correct in saying that the collector current is almost completely controlled by the (collector) load resistor in saturation. Your question gives you the collector emitter voltage as 0.2 which makes the voltage across the load as (5 - 0.2) or 4.8 volts, by your own (correct) equation. So you have simply done this sum incorrectly. You know the base voltage and you know the supply voltage, this is dropped across the base resistor and you know the gain since the transistor is just at the onset of saturation, ie just leaving the linear amplifier condition. So you can calculate the base current by dividing the collector current by the gain. Ohm's Law will then give you base the resistor value.
-
Which was rude because you lectured me about reading a post properly, whilst totally ignoring mine in your alleged reply. I had stated clearly that There is no universal present and implied that there is therefore no 'The present', as you had been calling it. Nevertheless you quoted my words and then carried on as if I had not posted anything. I would be happy to explain or expand on my assertion if asked about it, but I was not. It was not even graced with a denial or refutation. It was simply ignored.
-
1) Rudeness is counterproductive. I am well satisfied that, although I sometimes make grammatical or spelling errors my standard of English compares favourably to that you have shown in posts here. All I am trying to do is find out what you really mean when you make those outrageous claims such as space is time, then disown them 2) I did not say you did make that implication, I was addressing String Junky when I made that assertion.
-
This is even more incomprehensible than your previous statement.
-
OK so what exactly does the statement isn't space itself not a universal present mean and does it matter whether it changes or not? Are you asking if space is time? SJ +1 for a correct and nicely short comment. But it also implies something more, it implies instantaneous action at a distance.
-
Do you not read your own thread? This one is not quite 2 days old. There were references in both my posts, which were quite recent. I could feel quite insulted.
-
@John Lesser I see you are quite unable to address my comments.
-
I am not interested in your squabble with others here, but I am disappointed in your total disinterest in my (only) post#109 before this one. Eddington was the first man to articulate that there is no 'Universal Present', even if he was not the first man to realise this. (Faraday was the originator in his famous letter deposited with the Royal Society March 12th, 1832 An observer at one point in the universe will record a different 'present' from the 'present' recorded by an observer at any other point. Einstinian relativity is not necessary to understand this. I am trying to dig out the Eddington reference for you, where he develops this idea very clearly.