studiot

Do you not read your own thread? This one is not quite 2 days old. There were references in both my posts, which were quite recent. I could feel quite insulted.

@John Lesser I see you are quite unable to address my comments.

I am not interested in your squabble with others here, but I am disappointed in your total disinterest in my (only) post#109 before this one. Eddington was the first man to articulate that there is no 'Universal Present', even if he was not the first man to realise this. (Faraday was the originator in his famous letter deposited with the Royal Society March 12th, 1832 An observer at one point in the universe will record a different 'present' from the 'present' recorded by an observer at any other point. Einstinian relativity is not necessary to understand this. I am trying to dig out the Eddington reference for you, where he develops this idea very clearly.

I like Eddington's story of the cigars as a way of avoiding the acceleration in the twin's 'paradox'.

I'm glad to see strange mentiones manifolds, though I haven't looked into his references. This is because you can't have an everywhere smooth vector field on a spherical shell. (The Hairy Ball Theorem) This is important for instance in applying the NS equations to the Atmosphere. The reason for the ban on divergent (and convergent) fields is that there must be a singularity at the point of divergence (convergence) ie a sink or source

Yes I know the mass starts off in its initial position. That is a definition of initial position. But where is this initial position? And what of the spring? What is its condition? Come on, all the equations on earth are useless without the proper boundary conditions as well. I suggest you leave the location of the zero point (origin) until after the boundary conditions are fully specified, there is much to be said for measuring from the charged plate. Usually when analysing a system either The system is in a neutral condition in which case an outside agent acting once only is invoked to provide an initial displacement and the system then follows its trajectory controlled by the system forces. or The system is held at some point in the trajectory and released at time t = 0 and the system again follows its trajectory. A linear system will repeat the same trajectory over and over. But this system is non linear and I think there is the possibility that the neutral point will be displaced along the horizontal axis with each cycleand that each cyle will be different. So what I think you are saying is. The mass is attached to the unstretched spring (although you have not said if the spring can work in compression. Before t=0 no forces are acting The charge is somehow 'switched on' at t=0. The electric attractive force E causes the mass to move towards the plate, stretching the spring which provides a restraining force S. Now E increases as a second order quantity of displacement, whilst S increases as first order. So even if E starts from a lower base than S (depending upon the constants involved in the boundary conditions) it will eventually overtake S and from that point S will not be able to return the mass towards its original position.

Upon rereading all the posts and the title, I owe you an apology, Sriman. Nowhere have you mentioned simple harmonic motion, just harmonic motion which is different. However as I already indicated you have not convinced me that the mass will move at all, let alone oscillate. You should start by considering the Physics, before throwing in equations of any sort. I think this applies to some other posts as well. For example the nature of charged plate is important, certainly the distance dependence of the electric force is not as anyone has as yet stated. If the plate is large enough to be considered 'infinite', then the force is independent of distance, ie it is a constant. If the plate is of finite dimensions then at a large enough distance from it the attraction does indeed approach Qq/z2, but the true relationship is subject to [math]\left[ {\frac{z}{{\sqrt {\left( {{a^2} + {z^2}} \right)} }} - 1} \right][/math] Where z is the distance from the plate and a is the radius of a circular plate. Then we must consider the spring. Is the spring able to be compressed or not? If so then the spring force may reverse in direction at some point in any motion. Finally there is the starting position. Are we starting from an unstretched spring and, holding the mass in position and then releasing it, or somehow suddenly switching on the electricity? Or are we starting from a position (if one exists) where the restraining force of the spring exactly equals the electric force of attraction. If so why will the mass move at all? It is clear that there could be different equations in operation at different points along the axis connecting the spring foundation and the charged plate and that some of them may depend upon the dimensions of the system. So this is the last time I will ask you to specify properly.

I think a big problem for students is relating theory to practice. A few practical examples can bring out the important principles and provide a lot of fun. A hammer, nails, a wooden post and a lamina to nail to the post can demonstrate the difference between what happens when you apply a moment, (via a single force) and when you apply a couple. A more sophisticate experiment is as follows. Consider sharpening a chisel of thickness 4mm. The chisel is applied tangentially to a rotating grindstone of diameter 200mm and coefficient of friction 0.6. The chisel is pressed against the surface of the stone with a force of 10N and the frictional force is resisted by axial support at the other end of the chisel. Now the normal force pressing against the grindstone produces a normal 10N reaction on the chisel blade. Neither produce moments in the stone or chisel. The frictional force of the blade against the stone is 6N and acts tangentially so it applies a moment of 6*0.2 = 1.2 N-m, opposing the rotation of the stone. The counter frictional force acting on the chisel blade, also 6N, is balanced tangentially by the axial support force supplied to the other end of the chisel. But these two forces are not coaxial. The support acts along the centreline 2mm from the contact surface. The friction acts in the opposite direction along the contact surface. These two forces form a couple about the tending equal to 6*.002 = .012 N-m So the turning effects are not equal by a long margin.

Jamsmith wisely asked about "the turning effect of forces" and it is quite true that there are several different and distinct mechanical effects associated with turning. So it would seem to me highly sensible and desirable to identify each of these effects with a unique name. Unfortunately too many mix up the available different terms to create the general confusion, particularly for beginners, that holds today. So Perhaps a little history might help? Ca 250 BC The mechanics of turning effects was known to the ancient world for example the principle of levers attributed to Archimedes. 1725 The term moment was introduced and formally defined by Varignon in his book 'Nouvelle Mechanique.' “The moment of a force, P, about a point O is defined as the product of that force into the perpendicular OM drawn to its line of action from O, this perpendicular being reckoned positive or negative according as it lies to the left or right of the of the direction of P." Varignon's theorem holds to this day and may be found on Wikipedia. 1750 – 1804 St Vennant investigated the torsion of prismatic bars and posed St Vennant’s Problem. He did not however introduce new concepts in turning. 1804 -1806 Poinsot published his book 'Elements de Statique' and the theorem that bears his name. This introduced two things. He defined and introduced the term ‘couple’ and the theorem which states that in 3 dimensions any system of forces may be reduced to a single force plus a couple, in a plane perpendicular to the line of action of the force. He clearly defined his couple to exist in a plane. 1912 Lamb, one of the most prominent applied mathematicians of his time, proposed that the term ‘torque’ be introduced to replace ‘couple’ Lamb 'Statics' p52. “Since a couple in a given plane is for the purposes of pure statics sufficiently defined by its moment, it has been proposed to introduce a name torque or twisting effect which shall be free from the irrelevant suggestion of two particular forces.” This suggestion was not, however generally adopted. Indeed the three most influential texts ( in this subject) of that era and since carried on as before. 1926 Love ‘A Treatise on the Mathematical Theory of Elasticity’ 1936 Southwell ‘Theory of Elasticity’ These both refer to ‘Torsional Couples’ for the 3D effects described in St Vennant’s Problem. 1934 Timoshenko published the third standard text, ‘Theory of Elasticity’ and clearly establish torque in this 3D role. In fact most authors in the second part of the 20th century have followed the notation set by Timoshenko in elasticity. I haven't ventured beyond the first half of the 20th century because nothing new has been added since. It does bring out one other source of confusion. The difference between twist and turn, which is even less often correctly stated. I usually try to associate the Ts Torque, Torsion and Twist.

And I thought perhaps you were using the European convention, not the American one, which is confusing. A couple has the property stated in your last line. The moment of a single force is the different about nearly every point in a plane containing the line of action of the force. It is zero at every point along the line of action. A couple is the same about every point in the plane in which it acts. There does not have to be any material body at the point of action of a moment or couple.

In the water sprinkler, the water exits tangentially to the spin circle of the spinner. Consequently object A (the water) exerts a moment on object B (the spinner) , about its central mounting. However, as you have just observed, the spinner exerts no moment on the exiting water. Normally the spinner incorporates balanced pairs of nozzles so actually generating a couple rather than a simple moment. In the catherine wheel, there may be only one exhaust and therefore a simple moment, rather than a couple, is generated.

Go on?

I am guessing that you are referring to the resonant frequencies of pipes due to standing waves in the pipe. A closed end must have a node of the standing wave An open end must have an antinode. So for your question the fundamental occurs when you have one node in the middle and two antinodes, one at each end. The distance between adjacent antinodes (or nodes) is one wavelength, so the length of the pipe corresponds to one wavelength of the fundamental. Obviously the first harmonic you can have has two nodes and so on. Can you work out the relationship between the length of the pipe and the wavelength of the harmonics now?

Jamsmith Oh ok, I am grateful to you for your more precise discussion. Does it work like this? How does it apply to a catherine wheel or a lawn sprinkler?

I think you are trying to make this too complicated and should go back to the basics of SHM. You have too many terms in your equations for SHM. Further you have not responded to my hints in post#3. Your equations are overcomplicated because you conditions are inappropriate. You have yet to place the mass at the beginning of then process or establish what is meant by 'the mean position'. Bender asked you to state the original question you are trying to solve as written. Please do so as I wonder if you are not missing something out? Quite separately, I have started a thread in Feedback to try to get some help with placing images here.

This extract is from a recent thread; it refers to an issue that is by no means unique to that thread. I don't know how incorrect orientation could arise and was obviously not the poster's intention. Whether it was due to the origin of the pic being a mobile phone or tablet or something here at the forum. When the issue is resolved perhaps it could be flagged up in some way to help others in future?

Well spotted, thanks, +1. That was an embarrassingly silly slip.

Good evening Kevin, and welcome to SF. You certainly seem to have got into a tangle with this one,despite a lot of correct thinking. Is it homework? We have special rules about homework help. http://www.scienceforums.net/topic/75772-read-this-before-posting-in-homework-help/ Anyway Yes the first step is to convert all to the same units and 104 picofarads equals 104 * 10-12 = 10-8 = .01*10-6 farads or 0.01 microfarads. I laboured this because you seemed uncertain. All four capacitors are actually in parallel. If you look carefully, you can see that each capacitor has one connection directly to each terminal. A good way to see this is to delete three of the capacitors, but leave all the wiring intact. It is then easy to see that the remaining capacitor is directly connected across the terminals. So you need to simply add up their values as you correctly surmised. So, working in microfarads, we have 0.1 + 0.01 + 0.001 + 0.01 = 0.121 microfarads as your lecturer said. As another tip for a more complicated circuit. The right hand two capacitors form an easily recognisable parallel pair So combine these first to one equivalent capacitor before dealing with the crossed over ones. Then you can see that this equivalent capacitance is connected across (ie in parallel with) whatever the net result of the crossed over capacitors is. In this case they are also in parallel but they may not be for a more complex circuit. So you work your way through in simple steps, reducing the complexity wherever you can. It takes some practice to sort out when something is in series and when it is in parallel. Two further tips. Label your diagrams clearly and unambiguously so C1, C2, C3 and C4. This makes it so much easier to refer to the elements when someone is discussing them. Secondly this site allows you to write exponents directly using the superscipt and subscript icons in the entry box toolbar. That is such a boon.

Can you please post your pics the right way up? It is a nuisance to turn them round. You have not made it clear why there should be any oscillation at all. In other words why will the spring not simply stretch until there is a balance between the electrostatic attraction and the spring force? Note I am not saying there will be no oscillation, just that you haven't established the conditions for it to occur.

So are you only referring to gravitational mass or did you miss my post?

Are you sure you do not mean negative effective mass? This is a well documented and respected concept that can be used to explain some results for example in the Hall Effect.

There is another misconception that underlies this (OP) question and is evident in many of the replies. This is forgetting that the centre of mass of a rocket system does not move or that a body cannot spontaneously propel itself through a void.

Good morning, Nancy and thank you for your contribution. Since you haven't asked a question I will ask one. Entropy may change in the formation of a snowflake, but what about symmetry? Does it change and if so, does it increase or decrease? The reason for the correct answer to this stems from the same reason that a snowflake is more 'ordered'.

In which case surely your X and X' and the flatlines beyond them should be on the zero line? Initially said said that the acceleration was initially positive up to O and then negative afterwards, so I would expect to see your triangle part above and part below the line. A word about English and terminology. In ordinary English massive means having very large mass, which is as you seem to have used it for M1 and M2. In scientific English massive means possessing any mass at all, however small, so a neutron or a spaceship is massive, a photon is not. In circumstances like these the neutron or spaceship are called the 'test mass' in scientific English. Finally you have (correctly) posted in the classical section and refer to Newtonian mechanics. But even in Newtonian mechanics you need to consider the motion of M1 and M2 as well. Why would m pass along line XX? By the time m has reached the midpoint between M1 and M2, they will have, in general, moved somewhere else unless all three objects are tied to some other (larger) one. This is rather like the Earth, the Moon and a spaceship all possess a common motion about the Sun so we can make the motion assumption you have made as the spaceship moves across between Earth and the Moon.

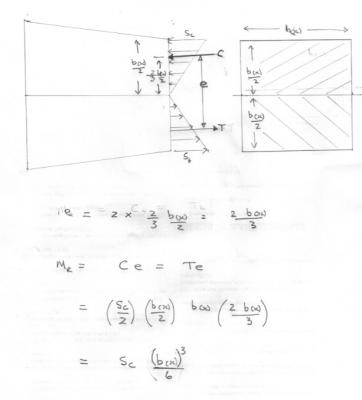
I am going to start this again to correct some errors you have made right at the beginning. Is this homework or are you trying to understand something you copied (wrongly) in class? Or are you struggling with English? These questions are meant to help since your first equation is impossible. If W is the moment of resistance then it does not have the dimensions of L3, which the equation you have written does. I will derive the correct equation, using the attachment which shows a section taken through the body at . The moment of resistance is defined as the moment resisting the couple generated by the compression © and tension (T) forces acting longitudinally within the body, due to applied stresses (Sc and St). By horizontal equilibrium C = T and the couple = MR = Ce = Te where E is the distance between the forces C and T. Since the stresses increase linearly with distance from the neutral axis C and T act through the centroid of the stress triangle as shown. This is at a distance 2/3 of the way from the neutral axis to the outside edge in each case. That is 2/3 of b(x)/2 since the neutral axis is halfway between the edges. So e is twice this distance. Now Sc and St are the maximum stresses, found at the edges. The average stress over the whole area is half of this ie (0 + Sc)/2 and (0 + St)/2 The Forces, C and T are found by multiplying the average stress by the area, which is shown in the right hand diagram as b(x)/2 *b(x) in each case. Thus we correctly find that the moment of resistance equals the max stress times (b(x))3/6. Please confirm you have understood this so that we can continue.