studiot

See how easy it is for misunderstandings to arise? I'm not Gary - he is a Professor formerly at Yale now at Pomona. and the author of the Applied Statistics book I referred to.

This is the first time I have looked at this thread as it concerns a subject area I am not usually interested in, but seems to have generated a deal of activity. I have two things to observe. 1) The issue of cutting / pasting and links. The settings on this and some other sites interact adversely with the settings on some windows computers so that the quote button and the paste function do not work. We have more than one thread (including one of my own) involving attempted help from the administrators, moderators and others but despite all the suggestions I still have one Toshiba Satellite Pro laptop that originally sported Windows 7 (now 10) that always suffered from this issue, which has never been resolved. I did resolve it on a Dell Vista machine by reluctantly using a different browser and this may be your only option as it presents a barrier to effective communication and is a bloody nuisance as well. Alternatively perhaps you can make one (trial) post from a different machine just for the links? 2) After 5 pages of squabbling where everyone retreated to isolated fortifications and pulled up their respective drawbridges I have learned that the OP wants to discuss alleged indications that large scale drug trials are somehow becoming less effective. This is straightforward applied maths that does interest me and there has been significant level of publication over the last 10 years or so about this. Both by Doctors https://en.wikipedia.org/wiki/John_Ioannidis https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1182327/ and by other acedemics Standard Deviations - Flawed assumptions, tortured data, and other ways to lie with statistics. Gary Smith I look forward to the OP response, including references to some real material to discuss. Dave, if you are still having trouble pasting in then I will see what I can do to help, though not with vague invocations to perform searches.

You need to provide sufficient information such as the relationship between l and b, and the loading conditions. Short stubby beams behave differently from long thin ones. Since the beam is tapering the loadings also play their part.

It's best not to argue with the referee. I understand your technical point and it's wrong. Have you never played 'tug of war'? There is no reason why a 'pull' can't be the resultant of two or more 'pulls'.

I don't think anyone will mind now, the question was so long ago that the OP cannot claim credit at school for it. There have been 163 views so we are addressing others who may like to know.

That's correct, Sriman. So can you complete the proof? Can you also complete this second one? http://www.scienceforums.net/topic/103844-circles/#entry975863

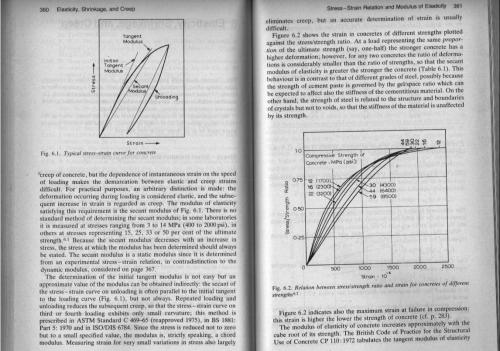
The chord modulus - also called the secant modulus. Last time I looked there was no standard method - which is why this extract says you should always state the points it is taken from.

Yes but it depends what you (and the OP) mean by "The Rocket". I am simply trying to point out that this is not a fixed object but is continually changing throughout the flight, unless you include the exhaust. Which I suppose is another way of say the same thing.

Reconstruction of past events and periods can be difficult and complex. Sometimes different indicators point in different or even opposed direction. First here is an extract about Chicxulub from a book that is a masterpiece of balancing all the conflicting evidence. This suggests that there is definite geophysical evidence for the activity reaching and affecting the mantle, though there is no suggestion that the meteorite survived even partially intact, like a bullet. Now to suggest that shock waves from this event which was effectively instantaneous somehow initiated up to a million years of successive lava flows require that it occurred before the lava. These recent references suggest otherwise. The impact http://www.livescience.com/26933-chicxulub-cosmic-impact-dinosaurs.html The Deccan https://www.princeton.edu/geosciences/people/schoene/pdf/Schoene_Deccan-Traps_Science2015.pdf Returning to the book I referred to unfortunately it is mainly about the Permian/Triassic boundary extinction but does provide an unbiased examination of the available evidence at its time of writing for other significant extinction effects, including the KT one in question. The techniques and trains of thought are worthy of examination. Paleontological, paleobotanical and so on evidence should be examined in both land, sea and air enviroments as well as evidence from inert matter both in type, disposition and mechanical, chemical and or thermal disruptions. Any proposed mechanism should be tested against the known geographical distributions of the land masses at the time of invocation of that mechanism. Are you talking an S or P wave? I can see the idea of an S wave temporarily opening a preexisting weakness to allow the exudation of magma, which then forced a widening of the breach and further outflow. Do you mean a true shock wave, which is the result of something material travelling fast than the local speed of sound, or something different? I agree with Argent the language is rather over dramatic for a scientific discussion. Remember also that the proposal is a hypothesis; a theory is rather more.

Thanks sensei +1

You have been told that the moon does rotate, but not like the Earth due to a phenomenon called tidal locking. So to complete the final part of this jigsaw. First why does the Earth (or moon or other body rotate at all?) Well during and after the formation of any substantial body in space other (smaller) bodies crash into it. Whether they coalesce with the body or just bump into it they must hit it off centre which means that the collision exterts a moment about that central axis. If all the collisions are from random directions they will tend to cancel out over time. But if they are mostly from certain directions, as in the early solar system, over time this builds up to generate a sizable rotational speed and there is not much in space to cause friction so the rotation will last a long time after the period of planet building has occurred. So we have a body like the Earth, which is slowing down, rotating about its axis, but having substantial rotational momentum The density of the Earth is 551 5510 compared to the Moon which is only 334 3340 kg/m3. Edit see post7 Coupled with the huge size difference between the two bodies this leads to a huge difference in stored rotational momentum. I will leave you to calculate the difference. As strange noted, so far gravity is not involved, but introduce that into the situation and you enter the interaction between two spinning bodies via the tidal locking mechanism when the Moon became captured by the Earth's gravity.

You can't change the rules half way. A rocket is basically a small payload on top of a large fuel tank. The fuel is often 90% of the mass of the rocket. At any one time the payload plus remaining fuel is being propelled forwards thus the mass of this combination diminishes rapidly with progress. It is true that [math]KE = \frac{1}{2}m{v^2}[/math] But m is a function of v or the other way round. So you need to develop a mathematical statement of this relationship to assess the KE of the part travelling forwards.

Then you will realise that the mass of the rocket is not constant.

Your title is a good one, because I think this is a straightforward misunderstanding. Therein lies your difficulty. Yes the thrust (a force) is constant. And if we take gravity as constant over the flight The same acceleration numerically happens in each second of the flight since force is constant. So each second the rocket gains say 5 m/s (or whatever) velocity. So the velocity gain is additive not multiplicative as you have in your '20 times' But of course if the acceleration is a (a + a)2 = (2a)2 = 4a2 and so on for higher powers. It is the difference between an arithmetic progression and a geometric progression. BTW I also wonder if you actually realise what force is doing the work. It is not the thrust alone.

Exactly and where did this equation come from? I have asked you several times what sign convention you are using and tried to make it fit, but you have not replied. Do you know what a sign convention is? Do you understand that the image is real and what this means? I can only help properly if you answer my questions - they are not tricks they are meant to help.

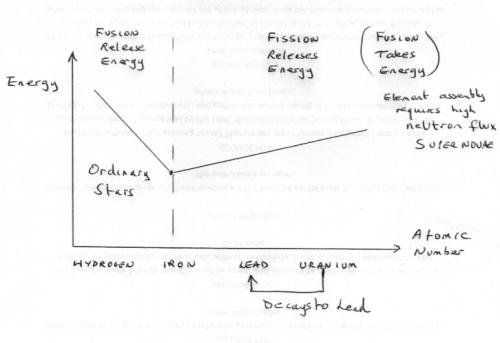
This is a good question and to answer it you need to look at what is well established in astrophysics, as well as a bit of nuclear physics. Here is a simplified diagram showing the important bits. This plots energy against atomic number and important elements are positioned along the axis. You will note that the energy is a minimum at the element iron (which has a lower atomic number than lead). I have drawn a dashed vertical line at this point. Physical systems tend to the lowest available energy state and the diagram shows that processes to the left of the dashed line that combine elements to form new ones release energy or lower their own energy states. These are of course, fusion processes and are the ones that occur in ordinary stars. The diagram also shows that to the right of the dashed line, to continue to assemble heavier and heavier elements (ie greater atomic number than iron) requires a supply of energy. Sufficient is not available in ordinary stars so elements heavier than iron are formed by another process. Such a process happens in a supernova. Ordinary stars are self sustaining for billions of years, but another important supernova process is the violent explosion they undergo. This ejects material in the explosion. So this provides freshly minted uranium for the inclusion in the formation of new planets. Looking further at the diagram you can see that all elements beyond iron have the potential to decay by fission with the release of energy. However not all elements readily do this. Uranium is the element of choice here and lead is pretty stable and one result of the decay of uranium. A great deal of readable further information is provided here. http://large.stanford.edu/courses/2013/ph241/roberts2/

There was a long discussion about this recently, so it obviously bothers some beginners. http://www.scienceforums.net/topic/59887-help-in-explaining-formula-of-kinetic-energy/page-2?hl=%2Bkinetic+%2Benergy#entry949583 my contribution started at post#39

Well you are getting there but your arithmetic is suspect. I make the chlorobutane 0.89/92.6 = .0096 moles or 9.6 x 10-3 moles. and the bromobutane 1.27/137 = .00927moles or 9.3 x 10-3 moles. Edit also present your calculation as a division not a multiplication please.

What was that a reply to, and what did it mean?

I am struggling to find your point in all that wordage. Especially as you have started two threads on essentially the same subject within half an hour of each other. http://www.scienceforums.net/topic/103942-a-question-of-delayed-choice-application/ Your comment that all points on a light beam are simultaneous to the light beam is essentially correct, but as to the rest What is your point sir?

Are chlorobutane and bromobutane liquids? If so can you not work out how many moles there are in 0.1 mL of pure substance. It will be different in each case. http://www.odinity.com/nucleophilic-substitution/

Two questions for you to think about/investigate. 1) Will the iodide replace/be replaced by both the chloride and the bromide? 2) How much of each reagent are you starting with?

I did say to watch out for the sign convention, yours is not the easiest. I also said to post your working - it makes it a lot easier to help that way. As it is all I can do is list the equations you should have, which you have not done. So Equation 1 do + di = 320 Equation 2 di/do = -1* (98/2) = 49 Note I have put the minus sign to a 1 here because neither the object nor the image distance is negative. The -1 tells you that the image is inverted, but you should also know (the equations don't tell you) that the image is real and therefore the image distance is positive. or di = 49do or do = di/49 Substituting first for do and then for di yields do = 6.4 di = 313.6 (These figures correctly add up to 320) Note that the quantity (do + di) is called the 'throw' of the lens and is often given the symbol T. Can you now use your third equation to calculate the focal length? and show your working please.

The OP actually did state one. However, only two equations were stated and three are available from the question information. Working it through I find that this does not work out to particularly simple numbers, but my figures place the object on the correct side of the focus. Solution strategy 1) Form two equations in the two unknowns, di and do, and solve. 2) Substitute these values into the lens equation you have stated and solve for f. Take care with the sign convention you are using with the negative sign in the magnification equation What is its significance? Post your working.

So did you find any congruent triangles, and if not, why not?