studiot

Mordred has the right idea and I'm sure we have lots of agreement on this subject. You can trade constraints for dimensions to some extent. For instance two dimensions, x and y, with no constraints, give you access to an entire plane. Adding the constraint y = x2 restricts you to a particular line. However it actually is very complicated. I had started to prepare a development of the subject but since discussion is live here is what I have done so far but please remember: It is not yet finished and the difficult bits are yet to come. Mathematically dimensions refer to the coordinate axes used to measure or describe something. Each axis is mathematically just an unrestricted list of numbers as mathematic says. This set up can be used in several ways. All the axes may carry the same weight or meaning, for instance a coordinate system describing length, breadth and height. This is pretty general and the basic system contains no restrictions. It acts as a self-contained entity with no reference to any other subject. Further each axis may be considered as representing a completely independent variable. We can use it to measure the size (or extents) of say a cube or other object wherever that object may be placed in relation to the axes. Mathematicians call this a 3 dimensional coordinate system and physicists would call it a 3 spatial dimensional system. We would say that the cube etc is embedded in this 3 dimensional space. We can restrict generality slightly to use coordinate system (1) for location or position. Coordinate system (2) is still 3 dimensional but yields slight more information, because of the restriction. We are interpreting the position of ‘points’ in this space. We can extend coordinate systems (1) or (2) by simply adding another axis of equal weight or meaning. This creates a simple 4 dimensional space that scientific observations suggest doesn’t physically exist in out material universe, but has mathematical existence for theoretical purposes. We can also extend coordinate system (2) by introducing a fourth axis with a different weight or meaning. For instance we can introduce a temperature at every point. In this view we can regard temperature as another variable axis that intersects our 3 dimensional position space. At any point all temperatures (T) are available but only one is ‘true’. So if the temperature somewhere is say 10o then the point (x,y,z,10) is regarded by the physicists as having physical reality or validity and the point (x,y,z, 20) is not. A mathematician, on the other hand regards the whole panoply of points (x,y,z,T) as being equally valid. Edit I hope Mordred can see where this is heading, but an aside on trading dimensions and constraints. Consider the standard parabola y2 = 4ax. This needs 2 dimensions to fit into, although it does not fill the whole two dimensions. It has one constraint. If we add another constraint (so we have 2) we can create it as a one dimensional entity: Introduce the 'parameter', t (which is one dimensional) and the constraints:_ x = at2 y = 2at we now have The parabola described by a single dimension.

This short statement is so profound - It carries vitally important information and is the key to resolving many of the misunderstandings on this subject. +1 It does beg the question as to why they are different or need distinguishing.

A really fun thing in modern chemistry that would be accessible to a high school pupil would be researching the B-Z reactions. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=B-Z+reactions&gbv=2&oq=B-Z+reactions&gs_l=heirloom-hp.3..0i22i30.1531.5281.0.6437.13.13.0.0.0.0.156.1374.5j7.12.0....0...1ac.1.34.heirloom-hp..1.12.1374.WJGDRL8OW1Q

Actually I would challenge this claim right from the start. I would claim "Nothing exists as far as anything exists" It is often said that fact is stranger than fiction and here is a case in point. A hole is a simple example of the existence of nothing. BTW I don't wish to participate in advertising a book, but am happy to offer proper debate on the subject here.

Gryoscopic fluid suspension is usually accomplished with a ferrofluid https://books.google.co.uk/books?id=Wr6l42rEizUC&pg=PA649&lpg=PA649&dq=gyroscopic+suspension+fluid&source=bl&ots=xoDrd0_oW-&sig=jFqQ4v7LKrU8uqpCytdwK__Voxw&hl=en&sa=X&ved=0ahUKEwiBmJrm9s3QAhWrAMAKHU2pDUAQ6AEIMzAG#v=onepage&q=gyroscopic%20suspension%20fluid&f=false Typical densities range from 850 kg/m3 for oil based ferrolfluids to 1400 kg/m3 for water based ones. http://faculty.washington.edu/finlayso/ferrofluid/Prop/all.html Was the 100lbs a guess or an actual weighing and did this include the can and was that Imperial or US Gallons and was the volume a guess as well? I ask this because of these comparisons. 1 UK gallon of water weighs 10 lbs and a US gallon about 8.4 lbs. By comparison with imatfaal's figures Earth and rock is about 2000 - 2200 kg/m3 Concrete is 2200 - 2400 kg/m3

If you liked GO you should read Gerald Seymour novels. But don't miss a word, he doesn't waste them or include unnecessary ones. Of course we have also had variations on the theme recently with the Divergent and Hunger Games films, and books. Science Fiction has long explored possible extrapolations of current situations I also found Billenium - J G Ballard Repent Harlequin said the Tic-Toc Man - Harlan Ellison very thoughtful.

Did it really take you all that time to read his works? Perhaps we should also include the CD in the study? https://en.wikipedia.org/wiki/1984_(For_the_Love_of_Big_Brother)

OK so you can't be bothered to work through my post#62. 'Nuff said, Have a nice weekend.

No my treatment was general, although the examples obviously had their own special characteristics. My post#62 was designed to help with you questions (especially your post#61 where you realised your thinking was going round in circles) if you can be bothered to work through it. In the question referenced above the speed in both the north and easterly direction was stated to be 1m/s. In what way did you think that was changed? Surely it was the direction that changed? Remember that Velocity is an instantaneous property. It can change from instant to instant but it has two sub properties viz speed and direction. Changing either changes the velocity. The important point in my post #62 is that you can replace any force with a pair of forces one of which only changes the speed and the other only changes the direction.

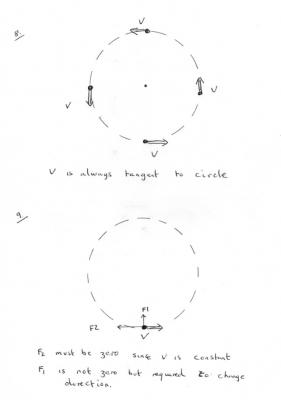
Since you put it so delectably How can I not respond? Here is a quick rough guide to Forces (and work and other stuff) To start with let us not worry about the motion (or lack of it) of a body. Just take any old body and apply any old force to it. So we have fig1. Now there is a pretty intuitive principle I hope you will take on trust without serious proof. You can replace a force with a whole bunch of forces but get the same overall effect. You can do this in lots of different ways with lots of different bunches of forces. (How do you get a bunch of forces? Get a bunch of grapes and eat all the grapes off the bunch. You are left with a bunch of forces) I have shown this in fig2 and fig4 In fig3 I have noted that a single force F may be replaced by two forces that act at right angles to each other and called them F1 and F2. These are often called components of Force F Forces at right angles to each other are special and we will meet them again later. fig4 also shows what we call equivalent force systems, they all have the same effect. OK so now we consider that our any old body had a (constant velocity) V as shown is fig5. We also know know that if we subject this body to some force system as in Fig 6, this force system can be replaced by a single force or alternatively a pair of forces at right angles, as shown in fig7. The last option - apair of forces at right angles - is the most interesting because F itself is at some random direction compared to the direction of motion. But if we align on of the forces, say F2, with the direction of motion the the other is at right angles to this direction. Now comes the clever stuff. F2 affects only the magnitude of the velocity (ie the speed) F1 affects only the direction of the velocity. So to change the magnitude we would apply only F2 and to change the direction only F1. Now to motion in a circle as in fig8 A body whirling round on the end of a string is in circular motion and if you do it inside your cab it is a bit like a goldfish in a bowl when viewed from outside the cab. The direction of the velocity is constantly changing, but the speed is constant So let us apply our pair of forces at right angles and such that one of them is directly opposed to the direction line. Since there is no change in the magnitude of the velocity this force must be zero. Newton's Law tells us that you need a force to change the velocity. So F2 is zero. But what about F1? Well the direction changes so F1cannot be zero. So for a body in circular motion, all the force that is applied must be at right angles to its direction of motion. (This force is the tension in the string and is called the centripetal force.) So didn't I also mention work? Well work = force times distance moved by/against that force. So for F2=0 W2 = 0 x Distance = 0 F2 does no work. But F1 is not equal to zero. However there is no change in distance from the centre since the radius of a circle is a constant. So W1 = F1 x 0 = 0 and also F1 does no work. So there is no work done by the centripetal force (or any other force) when whirling a body in a circle.

Essentially measure the signal before and after. This is a good reference http://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/beers1.htm

When the pipe diameter changes what is affected ie does the volumetric flow rate (Q) or the velocity change? You need the Bernoulli equation to complete the problem. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=bernoulli+equation&gbv=2&oq=bernoulli&gs_l=heirloom-hp.1.0.0i131j0l9.9672.12515.0.14375.9.6.0.3.3.0.125.639.3j3.6.0....0...1ac.1.34.heirloom-hp..0.9.733.EiwTpT6g1fU

The solution to the equation x - 4 = 0 is a single unique number. A solution to the equation x2 = 4 is either of a pair of numbers A solution to the equation sin(x) = 1 is one of an infinite list of numbers. The Schrodinger equation is a Hamilton-Lagrange equation of motion. As such it is an ODE in 1 dimensional space and a partial DE in 3 dimensional space. Do you know what a solution of such an equation is or how it is found? Do you know what it applies to or how many solutions there are? The solution involves the integration of two convoluted operators. As a result the answer is different depending upon the order of convolution. That is how the Heisenberg Uncertainty principle is derived. You may also seek stationary (time independent) solutions. That is how energy states are derived. Any old solution may not be used directly to generate probabilities. A solution may be converted to a probabilistic interpretation by normalisation.

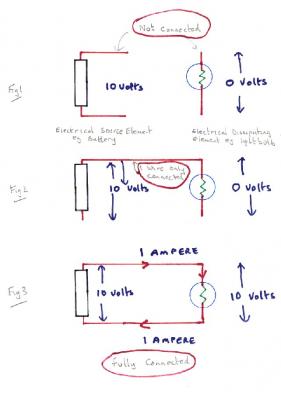
I said I would draw a diagram. These are the first things you need to know. I have built up the electrical circuit from Fig1 to Fig3, using an electrical source element (a battery) and an electrical dissipating element ( a light bulb). The battery is said to have an 'electromotive force' or EMF of 10 volts. This means that it maintains 10 volts between its terminals (shown as red wires) regardless of what is connected to it. There is a potential difference or PD of 10 volts across its terminals. Voltages are measured across an element. The lightbulb in Fig1 is not connected to anything and because it has no electricity source it has zero voltage across its terminals. There is no current flowing when there is no connection. The electric source has a voltage across it. The electric dissipating element has zero voltage across it. Note that both the battery and the lightbulb have two terminals. If we make one connection between one battery terminal and one lightbulb terminal as shown by a red wire in Fig2 There is no change. We do not have a complete circuit so There is no current flowing when there is only partial connection. The electric source has a voltage across it. The electric dissipating element has zero voltage across it. If we now connect the remaining pair of terminals with another wire we have a complete loop or circuit. This is shown in fig3. Current now flows through both the battery and the lightbulb and they both have 10 volts across them. Energy is now being transferred from the battery to the lightbulb and the current passes round the loop to return to the second terminal of the battery. The energy transferred per second is called the power and we have our first equation. Power = Current x Voltage = 1 x 10 = 10 watts or 10 Joules per second. P = IV So in 10 seconds 10 x10 Joules of energy will be transferred. Curent = Power x time I = PT Now we come to Ohm's Law. Firstly remember what I said backalong. The battery maintains 10 volts. This often causes confusion. This means that the voltage is fixed at 10 volts. The current is determined by the (electrical) size of the lightbulb. The electrical size is called its resistance and is measured in Ohms. Ohm's Law connects voltage, current and resistance by the equation V = IR The greater the resistance in Ohms, the lower the current that the lightbulb will draw. Since I have fixed the voltage using the battery we have 10 = 1 x R R = 10 Ohms. To recap Current moves (flows) through a resistor or other circuit element. Voltage may be zero or have some value but does not move. It is always across some circuit element. How are we doing?

Firstly why can't it be both? That is an entity in its own right that can be used as a 'meter'. It should be noted that the dimensions of one measurable physical property of (infinite) empty space are kg(metre)2(amps)-2(seconds)-3 in SI units Since there is no matter in empty space, yet it (empty space) has properties, matter alone is not enough to fully describe time. However it can also be seen to be connectable to other fundamental quantities so it can therefore be used (an is used) as a meter. Since you haven't specified what you mean by a 'meter' I will define it. A meter is a quantity that if known, by measurement or otherwise, can be used to deduce or calculate other unknown quantities, perhaps in conjunction with further known quantities.

Thank you for you points migL The point I was making is that A point, a line, a plane, a ball surface or its topological equivalent are all proper subsets (or subspaces) of Rn. With the exception of a point each of these have proper sub-subsets of their own. A point has no proper subsets. Curvature is defined by a calculus on a set, but you cannot have a calculus without proper subsets, so a(n isolated) point has no curvature of its own. For instance the Kappa you are talking about in plane curves or the Kappa and Tau I referred to (though not by name) in space curves.

Gentlemen, Surely all this quantum / historical stuff is over the top for someone who is just starting to learn Ohm's Law? Welcome to ScienceForums, physics is hard. OK so here is a rough guide to electrics. First and foremost you need to know that there are two viewpoints, just like with other subjects. A practical man's overview and the underlying science. It is good to get a bit of the practical overview before plunging into the underlying science. Then you will have some familiar material to work with. This is a bit like knowing that white powder A (sugar) will dissolve when you stir it into your tea, but white powder B (chalk) will not before studying the underlying scientific reasons for this. So in electric circuits we have two kinds of elements or components. Those that supply electrical energy (batteries, the mains and so on) Those that dissipate or utilise electric energy (light bulbs, heaters and so on) We measure the amount of electricity as the current in amperes or 'amps' for short. The voltage or volts for short does double duty. For sources of supply of electrical energy it is a measure of the driving force or electromotive force. For dissipators and users of electricity it is the 'voltage drop' you asked about. In order to get or force a particular dissipating element to pass a particular amount of current you have to impress a particular driving voltage across it from a electrical source. We say the dissipating element 'drops' that amount of voltage. Ohm's Law is the simplest relationship between voltage and current. Notice I haven't (needed to) gone into the more detailed physics behind this. Some diagrams would be helpful at this stage. If you want to continue perhaps sensei or I can draw some.

Since no one is interested in my contribution perhaps I should bow out of this thread. However on the way I would ask you to consider exactly what is meant by intrinsic and extrinsic and explain how a universe with the same laws as ours, but comprising a single point can support an intrinsic curvature. Furthermore it is worth observing that a single expression of curvature is only appropriate in 2 dimensions. In 3 dimensions there are two independent curvature expressions involved. Can you extrapolate to 4 dimensions?

With respect, this sounds like a rather rote response. I did not say we could use theodolites etc to measure the curvature, in fact I said the opposite. You can always regard a mathematical structure from different viewpoints, so you can always mathematically establish a dimension to set the radius in if you wish. Alternatively you can use the point to point properties in the working dimensions, as Feynman is proposing in his measurement of the Earth's radius. The plain fact is that space, in that direction, is non linear.

Capiert, if your way of thinking and presentation can help Frank to understanding, well done. So +1 for encouragement - these are the sort of posts we like to see. However I do not necessarily agree with quite everything you said and personally found it a bit rambling, though mostly along the right lines. Perhaps a little bit at a time might be better in future?

Hi geordie, This is a very good question, however I am not convinced by the Feynman quote. Although, like Einstein and Newton he was a tremendous genius, he, like them, was not always right in hindsight. That is not to say he did not have a point, but, as ever, life is a bit more complicated. His 'experiment' was a thought experiment and I will return to it at the end of this post. Here is a real world example of curvature and its effects, that has real implications in the real world. If we set up a theodolite at each of three points, A, B and C on the surface of the Earth and measured (the sum of) the angles of the triangle ABC we would not get 180o. We would get some larger number. This has practical significance in surveying. We do not need theoretically super accurate equipment this affects ordinary theodolites and surveying and is called 'spherical excess' Nor is it to do with the fact that the Earth is not a perfect sphere. The reason is due to the fact that the surface of the Earth is a curved manifold that cannot contain a plane triangle exactly. Both a plane and the Earth's surface are 2D manifolds 'embedded' in the same 3D space. The plane triangle, whose angles do add up to 180o. 'cuts through' the underlying 3D space, in which the 'curvature' radii and centres lie. In order to calculate the correct values we have to use the more complicated equations relevant to the 2D manifold that is the surface of the Earth. The choice of sphere or more complicated figure is the realm of Geodesy. As we are 3D (or 4D in spacttime) beings we have direct access to all the dimensions concerned and can make measurements in them. So we get different measurements depending upon whether we measure in the Earth's surface manifold or the plane manifold. [sidenote] This situation is the difference between 'local' and 'global' for many phenomena in Physics and of great importance in computer graphics where the approximation to any curved surface by a plane is known as a 'Coon's patch' [/sidenote] Back to Feynman. As we have discussed before, the 'curvature' in 3D space or 4D spacetime is different in that we do not have access to another dimension where the curvature might take place. All we have are the observed equations between points in our 3 or 4 D space which are not linear or Euclidian or flat - the appropriate terms sicne we have ramped up one dimension from a plane. So Feynman was not 'wrong', but his simplification was not totally 'right' either.

Your confusion arises because you expect a single unique definition for the word real. If you look in a decent dictionary (which might be a scientific one) you will find that most words have multiple definitions. Sometimes these definitions are variations on a similar theme. Sometimes they are quite different. And just occasionally these are opposed in meaning. As English speakers we have learned to cope with this using the context. English itself has sub divisions of some words A very common difficulty with the words real and reality occurs when folks try to shoehorn into one definition. Reality for concrete nouns is quite different from reality for abstract ones.

There are two quite different and incompatible definitions of 'particle' used in Physics. This incompatibility is fine so long as you do not try to mix the domains of definition as is being done here.

Here is a statement of Boyle's Law, in relation to this problem [math]{P_{100ft}}{V_{100ft}} = {P_{surface}}{V_{surface}}[/math] Even if you did not take the next step, you need to be able to take the data and present it in this form. Doing this should get you some marks. Saying I can't do anything gets you none. So can you rearrange this to give the ratios as asked? The gas laws are taught and used in Chemistry, Physics and General Science and many other branches of technical activity.

Since I do not have the time tonight to go through relativistic velocity addition I can only suggest ask Mordred or try to reread my links and get something more out of it. Nothing is moving at superlucent speed in any inertial frame.