studiot

Why should it? One answer was already provided in your link. My answer would be you can't make the physical connection to empty space, necessary for weighing anything. Your link also contains a fallacious statement in the section about the difference between a vacuum and a void. It claims that a void has no properties at all. This is untrue.

You posted a link to and quoted from a lot of material. Your point or question is specifically what exactly?

The question refers to the quote taken from your previous post and highlighted in my post # 8 In your terminology, x is not a number it is an element of the domain and x3 is not another number, it is an element of the codomain. You are the one who chose to introduce this method of describing a function. The point I am making is that the sign of the element (-3 in this case) in the domain is the same as the sign of the element in the codomain (-27 in this case), which was your specified definition of an even function in your post#7. This contradicts your statement in your post#9 which states that if n = 3, and therefore odd, the function is odd, since 3 is odd. As a matter of interest the range and the codomain do not necessarily coincide for a function.

Hello, jesse. Sriman is right you need a wider range of scinece than just chemistry at your age. How about the book of experiments? You may be able to get a second hand copy https://www.amazon.co.uk/Book-Experiments-Leonard-Vries/dp/0719503124 There were actually three in the series. You can download the first two here for free. http://www.arvindguptatoys.com/arvindgupta/bookofexpts.pdf http://www.arvindguptatoys.com/arvindgupta/bookofexpts.pdf

Sam you also need something else. Have a close look at a helicopter next time you see one (one on TV will do). The helicopter has a second spinning rotor, usually mounted in the tail. Have you given any consideration to why this is needed? To echo John Cuthber's comment can you tell us the purpose of this experiment?

You might like to consider if you have this the wrong way round. Consider f(x) = x3. If x = -3 then f(x) = -27 so the sign is preserved. Is x3 odd or even?

OK then I am happy to explain in more detail. First you need to know the difference between speed and velocity, Speed is just the numerical magnitude of the velocity, without regard to where you are going. So a speed is 10 MPH or 33 feet per second or 1 mete per second as in my example. Side Note you should (nearly) always provide the units in Physics. That gives meaning to the statement. Velocity always also includes where you are going ie the direction as well as the magnitude or speed. eg 1 metre per second north as in my example. Change of either the magnitude or the direction constitutes an acceleration. A body executing uniform circular motion is constantly changing its direction of motion, but not its speed. But it is accelerating.

Yes, you are indeed wrong. Have you studied the mechanics of circular motion?

The ball is in horizontal circular motion. As such it is continually subject to a force, which is continually changing its velocity (ie accelerating it) Yet no work is done by that (or by any other) force.

In Science we need to aim to be precise and accurate. Not everybody does so. I said nothing about the ball rising or falling or gravity in general. I did say the ball was on the end of a string. This should be a clue to why I noted your statement as only partly correct.

Not always. Consider a ball swinging on the end of a string travelling at 1m/s in a due northerly direction. How much work is done accelerating this ball to be travelling in a due easterly direction at 1m/s?

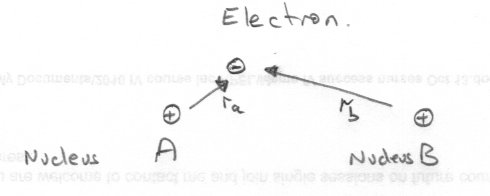
You don't need to get so complicated however if you want a physical interpretation rather than a description of how to do the maths. I asked what overlaps? This is because the integral arises when atoms combine to create a molecule by way of overlap of their atomic orbitals. The simplest situation is the two protons forming the hydrogen molecule. The lowest energy wave function in a hydrogen atom correspond to the 1s orbital and have the Schrodinger equation has a solution [math]{\Psi _{1s}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - r}}{{{a_0}}}} \right)[/math] If we now consider two hydrogen nuclei, A and B, influencing one electron as in the diagram The distances of the electron from the respective nuclei are ra and rb respectively. So the atomic wave functions are [math]{\Psi _{1sa}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - {r_a}}}{{{a_0}}}} \right)[/math] and [math]{\Psi _{1sb}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - {r_b}}}{{{a_0}}}} \right)[/math] Now consider a trial molecular wave function [math]{\Psi _{molecule}} = \frac{1}{{\sqrt 2 }}\left( {{\Psi _{1sa}} + {\Psi _{1sb}}} \right)[/math] Integrate this over all space [math]\int\limits_{allspace} {{\Psi ^*}\Psi dr} = \frac{1}{2}\int {{{\left( {{\Psi _{1sa}} + {\Psi _{1sb}}} \right)}^2}d\tau } [/math] [math] = \frac{1}{2}\int {\left[ {{{\left( {{\Psi _{1sa}}} \right)}^2} + 2\left( {{\Psi _{1sa}}{\Psi _{1sb}}} \right) + {{\left( {{\Psi _{1sb}}} \right)}^2}} \right]d\tau } [/math] which divides into the sum of three integrals. [math] = \frac{1}{2}\int {{{\left( {{\Psi _{1sa}}} \right)}^2}d\tau + \frac{1}{2}\int {{{\left( {{\Psi _{1sb}}} \right)}^2}d\tau + \int {\left( {{\Psi _{1sa}}{\Psi _{1sb}}} \right)d\tau } } } [/math] The first two are theoriginal atomic wavefunctions integrated over all space with suitable constants and equal 1 The third is called the overlap integral for obvious reasons.

No. The definition of an odd function is f(x) = -f(-x) The definition of an even function is f(x) = f(-x) That makes the zero function even, but the integral of the zero function over any interval is zero. There is no such thing as a trivial case in proofs.

From this and your other question it sounds to me like your need to pay close attention to your lecturer. She is right you need a crash course in stoichiometry, before you can progress in this stuff.

Earnshaw's you can pick up from the net. For Noether's, which is the one you most need, since it underlies pretty well everything else, try Emmy Noether's Wonderful Theorem Neuenschwander John Hopkins University Press for a first reading.

That's a poorly worded question and you have cut off the bottom of fig 1(b). So what is the dimension across the soffit of the trough?

So you are familiar with Noether's theorem, Earnshaw's Theorem and the Schwartz inequality?

Think about how the I beam is loaded. You are only considering loading to be applied on the central axis. In fact great effort is made in design and construction to make sure this is so. So think about how is any stress transferred to the flanges? This is explained in the bottom paragraph on the left hand page I posted in post#8, and drawn in the diagram on the right hand page. I will explain further about complementary stresses, but briefly they are stresses that are induced in planes at right angles to the primary stress or load to maintain static equilibrium, both force and moment. Have you revisited your original post about beam stresses? http://www.scienceforums.net/topic/100399-shear-stress-at-boundary-of-beam/

I also said you need think in 3 dimensions. Did your book derive the formulae for you? Yes the shear is along the beam as I showed, here is a better diagram, have you heard of complementary stresses?

The Schrodinger equation of quantum mechanics is an equation of motion. If the motion is fast enough relativistic effects appear. Paul Dirac was the first to present a version of the Schrodinger equation incorporating or corrected for these effects.

That last paragraph is exactly Euclid's view as also outlined in my sketch. He ignored the problem that you ask about, although Heath in his extensive discussion of Greek geometry within his translation of Euclid made it clear that the Greeks knew of it. The resolution came, as I also said, from Dedekind. You proposal is a synthesis. That is it tries to build up something substantial with objects of zero length. A way to do that did not arrive until Dirac. Dedekind's solution was analysis. That is to break down a pre-existing line into particles i.e. points. Formally he showed that there is always exactly one and only one particle or point at the joint of the partition of the divided line.

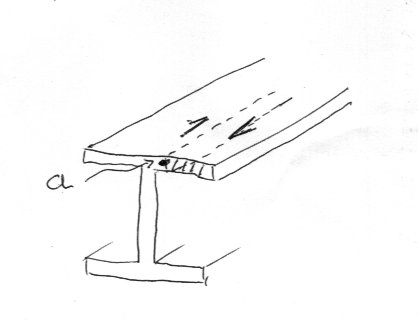
Here is a quick sketch I hop will help explain. The flange shear is the horizontal shear across the vertical dashed section through the point a in the sketch. The formula your book gives is derived by balancing the moments forces at a, due to the hatched section of flange to the right of a and forces to the left of a du to the main loading. Although the formula has almost the same form as the one in your other question, it is different in that the breadth of the beam is replaced by the thickness of the flange since the forces considered. are at right angles. You need to understand shear in beams in terms of three dimensions, not 2.

Could it be your arithmetic? At the boundary, [math]y = \frac{h}{2}[/math] So substituting [math]Q = \frac{1}{2}\left( {\frac{{{h^2}}}{4} - {y^2}} \right)b = \frac{1}{2}\left( {\frac{{{h^2}}}{4} - {{\left( {\frac{h}{2}} \right)}^2}} \right)b = 0[/math]

Err what overlaps then? I think this is the one that intests you From Atkins : Molecular Quantum Mechanics

It would be helpful to note that the definite integral counts areas below the axis as negative and areas above the axis as positive so the integral between limits may not equal the total area under the curve. In order to calculate the total area under the curve you do indeed have to split the range of integration and add up the absolute values of all the areas, regardless of sign.