studiot

Here is a properly peer reviewed scientific article concerninig the term chaos (and bifurcation) in fluid flow - open channel flow to be precise. If you look at the bottom you will see links to turbulent flow in channels. Turbulent flow is not chaotic flow. http://scitation.aip.org/content/aip/journal/pof2/6/6/10.1063/1.868206

I would be happier if you would substitute the word random for chaotic. The eddy coefficients (they may be variables as Sethoflagos pointed out) are defined in terms of a random variable, not a chaotic one. Chaotic flow regimes exhibit the bifurcation characteristic of certain forms of chaos. You also need to be careful not to allow your second statement about local flow changing as a function of time to confuse the difference between steady and unsteady flow. Turbulent flow can be steady.

What do you understand denser to mean? Density (of something) is that something per unit volume. So what is that something, and where does it live?

Yes but he that is at the expense of introducing c1 and c2 without saying what they are or where they come from. Only square matrices have determinants and by introducing the cross products into the original 2 X 2 matrix he has lost the squareness property. Note that a determinant is a scalar (usually a pure number). It is not a matrix.

There you are then you have answered most of my questions and you now need a crash course in differentiation methods. Integration is yet to be tackled. What you have listed in post#14 is basically the algebraic manipulation of derivatives and a few examples of use. Yes differentiation is basically algebraic manipulation. There are not many rules, you could probably learn enough to pick up enough marks to scrape by since you obviously understand basic algebra. (Not a path I'd recommend but it can be done and would be the start of your recovery).

Indeed this is what the current thread by geordief is all about.

There is nothing inherently wrong with the second matrix,or creating a column of products of other terms present elsewhere in the matrix, but it depends upon what you are doing. Matrix theory is part of linear algebra. Matrix operations are linear. Remember that each row of a matrix represents a linear combination of the entries (written as an equation if you like) so there has to be a linear combination a1 + a2 + a1a2 implied somewhere. You cannot use matrix operations to create the non linear a1a2 cross product. But you can include it a a specific term in the matrix. This is done in many branches of Engineering to create systems of (linear) equations involving non linear quantities. There is no special name for it since there is no opportunity to create these terms in matrix operations, they have to be 'planted into' the matrix.

I introduced the word 'manifold' and I think you have been party to discussions as to the meaning of this term before. Briefly a manifold is a set of connected points or objects or members. (There are some other considerations that do not need to concern us here) So you are hinting at this connectedness in your use of 'concatenation'. Connected means that you can get fom one point to the next by travelling only through points in the manifold. It further means there is some (known) relationship between the points such as an equation. Again we have talked about this before when I mention constrains in reference to a relativity thread. If you can get from one point to the next (following the instructions contained in the constraint equations), you have a path or line or track in the manifold. The surveyor is following his constraint instructions to provide a curved bellmouth at the road junction. The analogy is for understanding the idea that he can only use other points in his manifold, he cannot refer to external points which may as well be imaginary or not exist for him. The analogy is not mathematically the same as the actual expressions of curvature are different. The surveyor usually works to constant curvature, although there are occasions to use variable it involves a lot more calculation work. 'Curvature' in Relativity is of the variable type.

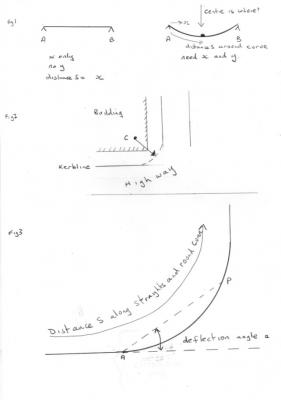
OK geordief, since I prompted this thread I had better post. I am going to reduce the discussion to one dimension for ease. That is instead of a rubber sheet I am using a rubber band. If I stretch the band horizontally between points A and B and ignore gravity for the moment I have the situation in the left hand of fig1. The band is one dimensional and lies along the x axis. So distances along the band are the same as distances along the x axis. However (and this is the key to the discussion) I am only interested in points that are on the rubber band. This becomes important as soon as I place a weight or force on the band to stretch it since we now have the situation in the right hand of fig1. The band stretches and is now longer than before. The distance along the band no longer equals distance along the x axis. So I say the band is 'curved', with a certain radius of curvature measured from a centre of curvature. But in order to do this I must introduce a second axis, the y axis. So I am now referring to things which are not on the band, and I repeat I am only interested in points that are on the rubber band. So we talk about the set S as all the points along the band and nowhere else. I have shown them taken in sequence, starting from A. This sounds all very well and pedantic for the rubber band since we have an available existing y dimension,to work in. But when we scale up to 3 (or 4) D we have never seen any evidence for the necessary extra dimension to work this way. The band is a one dimensional manifold. So I need a model that has this characteristic of only working with the points in the manifold of space(time). So let us look for an example in real life to act as my model. In fig2 I have drawn a typical surveying problem. Construct a curved kerbline at the junction of one highway with another. A builder might simply place a centre peg and swing a suitable arc from it, but what if the centre was inside a building? In this case the centre does exist, but is inaccessible. So our builder must stay on the kerbline and can only access points that are on it. This is how the model offers greater similarity than the rubber band. Knowing the characteristics of the curve (equivalent to having an expression for the value of curvature in GR), The builder can start at point A and calculate the 'deflection angle', he must turn around to get to point P which is also on the curve This is shown in fig3. So only the points on the curve and properties of those points (eg chord length AP) which are known or can be calculated are used. Obviously he needs mathematical expressions connecting points that are in the manifold as does the relativist for his work. The distance, s, along the kebline is known as through-chainage to the surveyor.

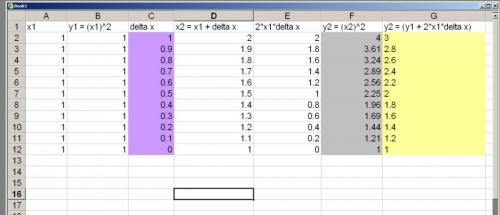
It would have been good if you had answered my questions from post#6. Particularly in respect of knowing what a function is. However this is the right idea, but a complicated way to start learning differentiation. We regard x and y as variables. This is they can represent any value within a given range. If we are given a value of x and some expression connecting x and y we can then calculate the value of y. So the value of y depends on the given value of x; it can no longer represent any value because of the expression. We say that y is the dependent variable. And that x is the independent variable since it can still represent any value we are given. We write this as y = f(x) or we can write the actual expression such as y = x2 I will use this simple expression as my example for differentiation. This might be the height of a hanging electricity cable, dangling between two poles. So as the poles get further apart the cable hangs down further. Now the whole purpose of calculus is to enable us to calculate desired results. We are usually more interested in finding the dependent variable, y, knowing the independent one x. The function y = x2 is also known as the primitive and the derivative is more properly called the derived function. You have probably seen it written [math]\frac{{dy}}{{dx}} = 2x[/math] Now I am going to write this expression in a slightly different way. [math]\frac{{\Delta y}}{{\Delta x}} = 2x[/math] Where [math]\Delta y = \left( {{y_2} - {y_1}} \right)[/math] and [math]\Delta x = \left( {{x_2} - {x_1}} \right)[/math] We can rearrange the expression for the derived function thus [math]\Delta y = 2x\Delta x[/math] So a change in y is approximately equal to a change in x multiplied by twice the value of x. So if we start from x = 1 and consider changes to y, resulting from smaller and smaller changes to x, we find that the above expression becomes more and more accurate. I have tabled this in the spreadsheet, starting at x = 1 and making smaller and smaller changes to delta x, from 1 down to to zero in 0.1 steps. As delta x gets smaller (the purple column) the value of y calculated from the approximate formula (the yellow column) gets closer and closer to the true value (the grey (column) calculated from the 'primitive'. So the error is 1 for a step size of 1 and 0.01 for a step size of .1 If you followed this motivation for why we bother with all this and you like it, then we can move on to the question of a limit, which it also demonstrates quite well.

Have a care What is the value of the determinant if a1 = b1 = c1 = 1?

Quite simple really. I asked what you man by an object. Using your pen analogy think of the pen. It has a 'length' from top to tip. But neither the top not the tip nor any point between are a pen. Yet these analyses treat objects as 'points' in respect of time.

I have never liked the rubber sheet analog as it introduces an inconsistency as well as an explanation/example. IMHO a far better analog is provided by the surveyors' technique of deflection angles, but that should be discussed in a separate thread if you are interested. Oh and I'm sorry , Strange, I do not have the information you request, but it would be interesting to know the answer if you find a definitive one.

Sandor told me that he has been ill lately. I'm planning to post the next stage of my suggested plan of action soon.

Part 2 in the extract I posted here, post#135 contains the beginning of the mathematics. http://www.scienceforums.net/topic/98845-models-for-making-sense-of-relativity-physical-space-vs-physical-spacetime/page-7 But your whole view of motion is too simplistic. I did ask what you meant by motion. Consider the fluid motion we are discussing this in another thread. Is fluid motion a property of the fluid as a whole (ie the flow) or a property of each individual fluid element or some combination? http://www.scienceforums.net/topic/99281-turbulence/

Have you lost interest in turbulence?

+1 for a gentle welcome

So it does depend on direction as well as speed. One can indeed. But there are many possibilities of formulae for this. Unfortunately not many treatments of relativity discuss why we use the quadratic we do other than to say 'it fits nature' (ie our observations).

I think you have identified the nub of the issue. +1 What do you mean by the object? An object, say the Earth, has definite extents in the three purely spatial dimensions. Yet you want to set up a (4D) coordinate system whereby simultaneously (in the mathematical sense not temporal) the axes are regarded as equivalent and yet somehow the properties are different for the spatial and time derived ones. If we identify extents in space why not in time or (ict) ?

So what would be the contraction at 45o to the direction of motion?

Have we done sniping now? I am more concerned with the lack of OP response to my post#23

What would be the contraction at right angles to its direction of motion?

First you need to be clear about the difference between Steady flow Uniform flow Laminar Flow Turbulent flow Vortex flow Rotational flow Irrotational flow. Brownian motion The main difference between laminar and turbulent flow is that the transport or transfer coefficients for laminar flow are molecular coefficients and are properties of the fluid, whereas for turbulent flow they are known as eddy coefficients and are properties if the flow. Flow is never fully laminar or fully turbulent, the total transport properties are the sums of the molecular and eddy coefficients and the ratio of these coefficients determine whether we call the flow turbulent or laminar.

I am not an astrophysicist, perhaps one here will answer authoritatively. Meanwhile look up sublimation of ice, which I believe is the process you seek. https://en.wikipedia.org/wiki/Sublimation_(phase_transition)

Considering the definition of boiling point The temperature at which the vapour pressure of the liquid is equal to the pressure of the gas above it the question has no meaning in a vacuum.