studiot

Yes this was the motivation for the question. Here is some more background. With reference to the diagram, consider the instantaneous coordinate frame of A with one spatial and one transformed time axis ct (I have kept it simple). The part light cone represented by the triangle EAC contains all the points that particle A could concievably attain and a sample worldline is plotted as a dashed line. This worldline must lie with EAC. Now consider observers situated at B, C and D, all moving relative to A. Each will have its own lightcone represented by a triangle in its own frame. But each will see time as dilated and length as contracted along the ct and x axes of A. So each will see the figure A sees as triangle AEC and the worldline as distorted compared to the view from A. Hence the question, as it will take me some time to plot it all out.

Touche +1

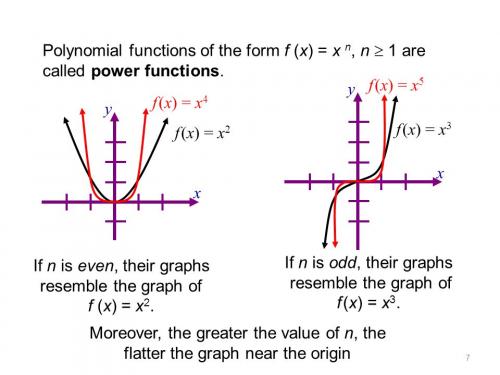
A bit odd?? But what about the other bit ie the rest of you? So you are really like most functions, the sum of an odd and an even function.

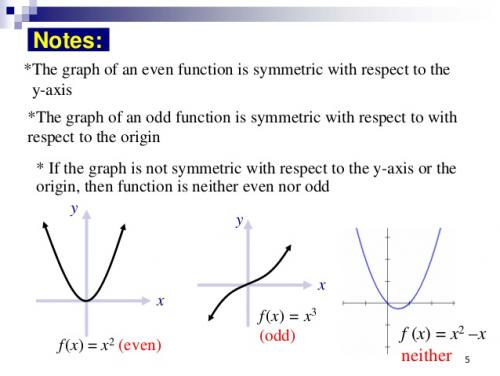
What is trivial does indeed depend upon the context. Remember it only takes one except to disprove the most elegant theory in maths. The zero function is y = 0 for all x. This is not quite the same as for instance y = ax3 which is odd for all a except a = 0, when it is neither odd nor even. It is a subtle point and I wanted to move on from towards noting that in general functions are neither odd nor even, but may be decomposed into the sum of an odd function and an even function. Odd and even have significance in science, in that they are examples of a wider phenomenon known as parity. Even functions have parity +1 and odd functions have parity -1 Parity is related to symmetry, so an even function is symmetric with respect to the y axis, x = 0 and an odd function is antisymmetric with respect to the x axis, y = 0

This is really Mordred's area. I have started another thread with a question that might help here so please watch for his response. http://www.scienceforums.net/topic/100764-a-light-cone-question-for-mordred/

Do you have an images of what a light cone of a particle B might look like, when measured in the frame of another particle, A such that A and B are in substantial relative motion?

Every point on the world line of a particle generates a new light cone. So considering several observers can generate a complicated tangle of light cones. It is important not to unintentionally include an assumption of some sort of absolute spacetime in consideration of these. A good question to consider here would be: How do the light cones from particles outside the light cone of some given particle overlap with the light cone of the given particle?

+1 for spotting the circular argument, Tim.

I haven't worked it fully through, but does not the substitution z = x2 dz = 2xdx [math]I = \frac{1}{2}\int {{e^{ - z}}} dz[/math] Not suffice?

Nicely put, Janus. +1

Yes indeed I missed the order reversal so your two posts are consistent. Sadly they are consistently wrong.

You are nearly there. Note I said completely isolated empty space. In a 'chunk' of empty space near a massive ( = body with mass, not necessarily a large mass) body g will not be zero. So I guess the question Frank Wilczek posed refers to this case where the empty space is not isolated. What he is saying concerns the influence of the container/boundary of the empty space, along with whatever lies beyond it. zbi I have answered your question precisely. You have not acknowledged the answer. So how can I proceed to explain an additional gratis remark I made for your benefit? But yes I can not only explain at least one property of empty space I can confirm my prediction by direct measurement.

I presume you are referring to a definition of weight, W as W = mg. The problem is that g is zero in an isolated completely empty space.

Why should it? One answer was already provided in your link. My answer would be you can't make the physical connection to empty space, necessary for weighing anything. Your link also contains a fallacious statement in the section about the difference between a vacuum and a void. It claims that a void has no properties at all. This is untrue.

You posted a link to and quoted from a lot of material. Your point or question is specifically what exactly?

The question refers to the quote taken from your previous post and highlighted in my post # 8 In your terminology, x is not a number it is an element of the domain and x3 is not another number, it is an element of the codomain. You are the one who chose to introduce this method of describing a function. The point I am making is that the sign of the element (-3 in this case) in the domain is the same as the sign of the element in the codomain (-27 in this case), which was your specified definition of an even function in your post#7. This contradicts your statement in your post#9 which states that if n = 3, and therefore odd, the function is odd, since 3 is odd. As a matter of interest the range and the codomain do not necessarily coincide for a function.

Hello, jesse. Sriman is right you need a wider range of scinece than just chemistry at your age. How about the book of experiments? You may be able to get a second hand copy https://www.amazon.co.uk/Book-Experiments-Leonard-Vries/dp/0719503124 There were actually three in the series. You can download the first two here for free. http://www.arvindguptatoys.com/arvindgupta/bookofexpts.pdf http://www.arvindguptatoys.com/arvindgupta/bookofexpts.pdf

Sam you also need something else. Have a close look at a helicopter next time you see one (one on TV will do). The helicopter has a second spinning rotor, usually mounted in the tail. Have you given any consideration to why this is needed? To echo John Cuthber's comment can you tell us the purpose of this experiment?

You might like to consider if you have this the wrong way round. Consider f(x) = x3. If x = -3 then f(x) = -27 so the sign is preserved. Is x3 odd or even?

OK then I am happy to explain in more detail. First you need to know the difference between speed and velocity, Speed is just the numerical magnitude of the velocity, without regard to where you are going. So a speed is 10 MPH or 33 feet per second or 1 mete per second as in my example. Side Note you should (nearly) always provide the units in Physics. That gives meaning to the statement. Velocity always also includes where you are going ie the direction as well as the magnitude or speed. eg 1 metre per second north as in my example. Change of either the magnitude or the direction constitutes an acceleration. A body executing uniform circular motion is constantly changing its direction of motion, but not its speed. But it is accelerating.

Yes, you are indeed wrong. Have you studied the mechanics of circular motion?

The ball is in horizontal circular motion. As such it is continually subject to a force, which is continually changing its velocity (ie accelerating it) Yet no work is done by that (or by any other) force.

In Science we need to aim to be precise and accurate. Not everybody does so. I said nothing about the ball rising or falling or gravity in general. I did say the ball was on the end of a string. This should be a clue to why I noted your statement as only partly correct.

Not always. Consider a ball swinging on the end of a string travelling at 1m/s in a due northerly direction. How much work is done accelerating this ball to be travelling in a due easterly direction at 1m/s?

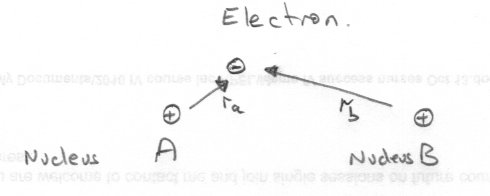
You don't need to get so complicated however if you want a physical interpretation rather than a description of how to do the maths. I asked what overlaps? This is because the integral arises when atoms combine to create a molecule by way of overlap of their atomic orbitals. The simplest situation is the two protons forming the hydrogen molecule. The lowest energy wave function in a hydrogen atom correspond to the 1s orbital and have the Schrodinger equation has a solution [math]{\Psi _{1s}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - r}}{{{a_0}}}} \right)[/math] If we now consider two hydrogen nuclei, A and B, influencing one electron as in the diagram The distances of the electron from the respective nuclei are ra and rb respectively. So the atomic wave functions are [math]{\Psi _{1sa}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - {r_a}}}{{{a_0}}}} \right)[/math] and [math]{\Psi _{1sb}} = \frac{1}{{\sqrt \pi }}{\left( {\frac{1}{{{a_0}}}} \right)^{\frac{3}{2}}}\exp \left( {\frac{{ - {r_b}}}{{{a_0}}}} \right)[/math] Now consider a trial molecular wave function [math]{\Psi _{molecule}} = \frac{1}{{\sqrt 2 }}\left( {{\Psi _{1sa}} + {\Psi _{1sb}}} \right)[/math] Integrate this over all space [math]\int\limits_{allspace} {{\Psi ^*}\Psi dr} = \frac{1}{2}\int {{{\left( {{\Psi _{1sa}} + {\Psi _{1sb}}} \right)}^2}d\tau } [/math] [math] = \frac{1}{2}\int {\left[ {{{\left( {{\Psi _{1sa}}} \right)}^2} + 2\left( {{\Psi _{1sa}}{\Psi _{1sb}}} \right) + {{\left( {{\Psi _{1sb}}} \right)}^2}} \right]d\tau } [/math] which divides into the sum of three integrals. [math] = \frac{1}{2}\int {{{\left( {{\Psi _{1sa}}} \right)}^2}d\tau + \frac{1}{2}\int {{{\left( {{\Psi _{1sb}}} \right)}^2}d\tau + \int {\left( {{\Psi _{1sa}}{\Psi _{1sb}}} \right)d\tau } } } [/math] The first two are theoriginal atomic wavefunctions integrated over all space with suitable constants and equal 1 The third is called the overlap integral for obvious reasons.