studiot

Although you have quoted my entire post#28 I am struggling to see the relevance of any of your reply to it.

A Radio Amateur's Licence? You would need some sort of licence to do this.

Fred, I am guessing that your question was basically how to squeeze the maximum data rate down a given link. I take my hat off to the ingenuity of engineers in the getting around the Shannon limit. It should be noted that this limit refers to a single communication channel. So any way of increasing the number of channels used to transmit the signal increases the data rate. Here is an extract from Wikipedia (have you tried it ?) Note that this says for single voice channel (ie one telephone line) the limit is 56k, as I said earlier. It also says that that single line is used as a multichannel line by a process I called frequency division multiplexing, earlier. This is how modern megabit rates are achieved. So that's one way to cheat the reaper. Some years back, the BBC used another method when they transmitter digital code, they called Basicode. This was very clever because it took an existing transmitted audio signal and superimposed the Basicode signal by chopping it up so the incoming audio signal looks (on an oscilloscope) rather like the audio I get from an old signal generator I have which uses the beat frequency technique to generate its output. This will work on either the radio or the television audio.

A good place to start looking is Ian Stewart's little book. Galois Theory Chapman and Hall Professor Stewart has a well deserved reputation for making mathematics understandable, without loss of correctness. You might also need Introduction to Group Theory W Ledermann Longmans since it is hard to do Galois without being doing Abel.

Thanks, Mordred for posting links to light cones, and cosmological stuff which is way beyond my knowledge. +1 I was going to post a discussion of light cones and once again stress that they are the boundary of a region which is fully accessible. Yes the hypersurface is lightlike, Michel do you still need my contribution on this? I can't help with the cosmology, except for observing that it clearly takes into account the simplistic comment I made about SR v GR and gravity.

Comments in red.

Isn't the lightcone the boundary of what is accessible?

Wikipedia was only the first reference in the link I posted. But as the subject is so popular Wiki is particularly strong here. You asked what is the 'shape' generated by the equation I gave (it also appears in Wiki in their usual highbrow form, they rarely go in for plain speaking) It is the equation of the famous lightcone hypersurface in Minkowski space. But remember that Minkowski spacetime is flat ie Euclidian ie unperturbed by gravity. That is special relativity. If you move to general relativity, gravity introduces further constraints that modify this. However the lightcone contstraint is a strong one, the gravitational one quite weak in most of the universe. The point is that, like the circle, we can put any number we like to any of the coordinates (x,y,z,t), the constraints simply prevent access to some of these. So it becomes a philosophical question, as with the circle, Is the rest of spacetime still there or for the circle is the rest of the pq plane still there? This is interesting because it is the obverse argument to the one about the existence of a hole, which requires surrounding reality (matter) to define it.

It might be a good idea to come back down to Earth and look at a few basics of modulation. 1) For analog signals there is a maximum depth of modulation possible for AM since you cannot 'modulate' the carrier below zero. This is not a restriction suffered by some other types of modulation, particularly angle modulation, which includes frequency and phase modulation. 2) Shannon's criterion can be bypassed by multiplexing techniques, time division or frequency division are common. This is how modern broadband signals squeeze more than Shannon down the phone line and also how modern (TV etc) broadcasting works. 3) Digital techniques are inherently more accurate and reliable than analog at the current state of technology. The reverse was once true but this has reversed. It does not mean to say that it will not reverse again. 4) Analog techniques and amplitude modulation techniques refer to different processes. You can have analog or digital signals transmitted via amplitude modulation. 5) The oldest data transmission technique is neither analog or digital but is still the most accurate and reliable. That is pulsed continuous wave, for example morse code.

First thanks for bringing my slip in post#16 to my attention. It is now corrected. The answer to your question can be found here. Wikipedia is good enough. https://www.google.co.uk/search?q=ivariant+interval+in+relativity&rlz=1C1AVNG_enGB673GB673&oq=ivariant+interval+in+relativity&aqs=chrome..69i57.9579j0j8&sourceid=chrome&ie=UTF-8#q=invariant+interval+in+relativity

The last slave I asked to check my work died of overwork.

The terms contra and co variant were introduced in the middle of the 19 century during the study of coordinate systems and it is this meaning that you are seeking. Be aware that mathematicians later generalised the concept to more abstract and general systems of algebra, called category theory and processes known as functors. Be glad you do not need these. Vectors and tensors have elements and strictly speaking it is these elements that exhibit covariant, neutral or contravariant behaviour, not the vectors, tensors etc themselves. So what is covariant, neutral or contravariant behaviour? Well since many people are put off by the notation and complexity when it is introduced with tensors let us look at the simplest situation - that of a single component vector or tensor. That's right you can have a single component vector or tensor say [a] This is useful because one component can only exhibit one of the behaviours, whereas a vector or tensor of higher order can have some components contra, some neutral and some co variant. OK so some concrete examples of this I am some 5 miles away from the controversial nuclear power station at Hinkley point. To put in a coordinate system, my map says that HP is 3 miles east and 4 miles north of me. Now suppose that there has been a leak and some of radiation passes over such that the dose, R, radiation units is equal to [math]R = \frac{{{\rm{Constant}}}}{{{\rm{Distance}}}} = \frac{a}{D}[/math] But the formula is given out by the french operator, whose map measures distance in kilometers is R = 5/D. That is a = 5 for them. To remedy the situation I need to modify their formula and I have two choices. 1) I can convert miles to kilometers or 2) I can keep working in miles and change the constant to suit. If I adopt (1) I will get a large number (8 kilometres) for D but the actual physical distance is the same. But the actual units on my axes are smaller since kilometres are shorter than miles. So R = 5/8 radiation units This is an example of contravariance. When I transform from miles to kilometers the variation in the size of the variable (larger) is in the opposite direction to the variation in the size of the units on the axes (smaller). If I adopt (2) then the dose R stays the same and I must alter the dose factor a to suit - in this case multiply it by 5/8, making the equation [math]R = \frac{5}{{D\,kilometrs}} = \frac{{5*\frac{5}{8}}}{{D\,miles}} = \frac{{25}}{{8D}}[/math] Which again equals 5/8 radiation units. But this time the variation (smaller in a) is the same as the variation in axis units (smaller). This is an example of covariance. A neutral component would be one that is unaffected by the transformation. This is called an invariant. So in the case of transforming a map in miles to one in kilometers bearing angles would remain the same. If this helps we can move on to look more deeply into the subject.

Thank you for the endorsement. Indeed I meant that they meet in space, but their measure of time is different. As I mentioned (x,y,z,t) perhaps some further clarification is in order, since they are not truly independent coordinates. Let us consider a simpler system to start with containing just p and q ie (p,q) for generality. If p and q are truly independent we can pick a point with any value of p and then choose any value of q we like without reference to the value of p. Or if you like, for every value of p there is a point corresponding to every value of q. Doing this of course generates the the whole pq plane. But Suppose I introduce a constraint, say p2 + q2 = k2, where k is a constant. Without the constraint the system has 'two degrees of freedom' ie we can independently vary two variables. With the constraint, x and y edit p and q oops! are no longer independent. In fact you may recognize the common equation of a circle and the points we are able to choose from lie on a circle of radius k. Most people automatically assume that (x,y,z,t) coordinates have four degrees of freedom as with the pq plane. But in a similar (though more complicated) manner there is a constraint introduced by relativity which is s2 = x2 + y2 + z2 -c2t2 So there are less than four degrees of freedom available and the variables are not truly independent.

Well it rather depends what you mean by constant. In vacuo the speed is the same for all wavelengths (frequencies) in all directions, and incidentally is the maximum speed for light. So we don't normally consider these as important variables. Introducing a material introduces complications. Firstly the material itself may not be homogeneous so the passage of light will be affected as the material composition changes. But even given a homogeneous material its effect may not be isotropic in that the refractive index may vary with direction. Finally the speed is now a frequency dependent quantity, in any direction, but is fixed or 'constant' in that direction for as long as the material remains homogeneous and the light frequency is fixed.

Robin, try this explanation of the twins. Call the stay at home twin A and the travelling twin B. A never leaves Earth. So A never arrives anywhere else. This is the crux of the difference. B leaves Earth B arrives somewhere else. B returns to Earth. So B travels within the universe from one place to another, visiting places in between. If we were to suggest that what B sees is equivalent to what A sees, but the other way round, then we would be just plain wrong. If we suggest that B sees the rest of the universe recede and then return to B, it would imply that the rest of the universe must arrive somewhere else. But B can determine when he returns, after consultation with A, that A never went anywhere. So at least a part of the rest of the universe did not go anywhere (ie did not arrive somewhere else). Suggesting that the universe recedes is the same as suggesting that B travels outside the universe. What swansont is suggesting in post#12 is that A's journey is not through space at all. It is only through time. In terms of Frames, A is in frame (x,y,z,t) and B is in Frame (X,Y,Z,T) A's journey is (0.0,0,0) ; (0,0,0,t1) ; (0,0,0,t2) ; (0,0,0,t3) ; (0,0,0,t4) ; (0,0,0,t5) ; etc On the other hand B sees his journey as (0,0,0,0) ; (X1,0,0,T1) ; (X2,0,0,T2) ; (X1,0,0,T2) ; (0,0,0,T5) Setting the X axis along B's journey to Betelgeuse, which he reckons is X2 distant. This makes the travel along the Y and Z axes all 0. The fact the two frame origins were momentarily in coincidence at the start is the result of synchronisation, but since there is relative motion between the frames there is no reason to expect them to coincide at any other event. What is happening is that they coincide in space and time the first event due to synchronisation , but the second time they coincide in space, but not in time since t5 is not the same as T5.

Are you still interested in this?

I have an old Dell (Vista) laptop I'm using for controlling things in a play and am trying to get a handful of keys to play particular sound files on demand, without leaving the Powerpoint screen. Any ideas welcome. Already tried Intellitype, but can't seem to access the keys, let alone reprogram them.

Duplicate post with this one. Answers there. http://www.scienceforums.net/topic/97453-organic-chem-help/

+1

Modern solder for both plumbing and electrical work is lead free by regulations. Partial separation can be effected by physical means (heating) but the residue will approach the eutectic mixture ever more closely. http://www.chemguide.co.uk/physical/phaseeqia/snpb.html If you are able to heat to gaseous states and conduct fractional distillation this would work. Otherwise you will need to find an acid that dissolves tin but not lead (why not the other way round?) and follow this up with some chemistry. But all these are hazardous procedures, there is no easy way.

Since you didn't reply to my answer to your question which was basically where does the extra angular momentum/energy come from that is gained by the plane on its southwards journey, I hesitate to bother further. However think on this. The energy comes from the aircraft engine having to work harder. As others have said it will need to adopt a suitable heading to counter/keep up with the westward movement of the Earth's surface and fly at an air speed (did you look this up as suggested, there is plenty on BigG) which is greater than that of the southward progress. This greater speed will result in the engines working harder.

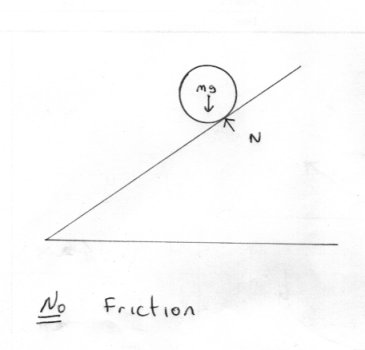
You gave two situations I started with the first and simplest. What causes the ball to roll if there is no friction? In the real world, air friction would be enough to turn it, but in our idealisation there are no such forces acting. Note that a vehicle or railway engine wheels will spin under the vehicle when driven from the centre axle without moving the vehicle if there is not enough friction.

Is this homework? You really need to explain the problem more completely otherwise people are left guessing what you mean. I am guessing that you are talking about a ball rolling down a slope from a standing start so the equation of constant acceleration applies with the downslope acceleration = gsin(x) so we have using vt = u + ft = 0 + gsin(x) * t Which is your first equation. But will the ball roll or slide down the slope?

swansont is correct, but perhaps to help you produce something closer to an appropriate analysis, here is a hint. Beginners often think that centripetal force is due to the circular motion and is somehow additional to the other forces that are acting. This is not so, it is the other way round, The circular motion is due to some force, in this case the one in the spring, and we call it the centripetal force. But this is the same force that is described by Hooke's Law, not an additional or different one. Does this help?

You are right to ask this as a classical physics question. Classically the plane is still subject to the Earth's gravity. Escape velocity is some 40 times as fast as your aircraft speed. It is also a good idea to revise the difference between air speed and ground speed, you seem to have blurred this distinction.