studiot

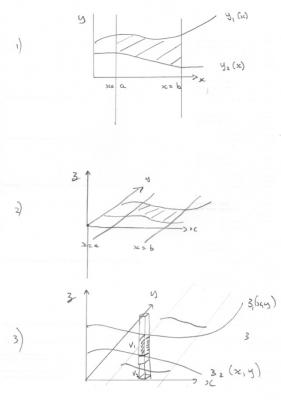
Please confirm the following with reference to my diagrams attached. Sorry for the quality of the hasty sketches. 1) Mark off an interval, ab, along the x axis shown by lines through a and b parallel to the y axis. Draw in y1(x) and y2(x) as the bounds in the xy plane. This defines a surface (area) in the xy plane. 2) Erect a z axis perpendicular to the xy plane showing the bounding area we are working in. I have shown this hatched. 3) Erect rectangular columns over this area from xy plane to the bonding surfaces given by z1(xy) and z2(xy) This defines the volume we are working in now for your function R The general wave equation is a connection between time and space which introduces an extra variable we have not catered for (time) To take time into account we have to account for the flux of R crossing the volume boundary as defined above, as well as the waves already within the volume. A more restrictive wave equation is the time independent equation of standing waves. If the waves are standing there is no flux across the boundaries so time may be discounted and a simple spatial volume integral employed.

The following 4 slides from the Cambridge University Physics teaching site may help you think about Imatfaal's comments as well as mine.

Forgive me but I can't see a c anywhere.

You are running ahead of yourself. Much of modern theory in this area revolves around the the difference between linear (euclidian) and affine spaces and transformations. This distinction is often not clearly drawn. Mordred mentioned rotations. There are also what are known as 'forbidden' rotations' we are important for non symmetrical (handed or chiral) objects. Operators (mathematically) are a particular way of expressing relationships (equations and so on) for convenience of mathematical processing.

Hmm, a difficult one we have thought about in our family. +1 Let us look back ways over history, at least over the time when society was rich enough supply youth with the time and resources for (I hate to use this word) leisure activity, on a widespread and general scale. In the late Victorian and post Victorian era, mechanical hobbies abounded. Meccano, Hornby and many others spring to mind. Model making was a hobby that carried on into adulthood and enormous effort was put into these. These hobbies also followed the development of technology. So steam gave way to IC engines and then to radio and then to amateur electronics, amateur computers (hardware) then software. In these and other hobbies there was a cycle of constructors and users. Photography is a really good example here. Some like to construct then get bored once they have built it, some really prefer to use and buy kit ready made. Amateur radio is a really good example. Not all these hobbies are scientific/technological. Fishing is the most popular sport in the UK. So why am I mentioning these? Well they have all displayed similar characteristics to those mentioned in the OP. Has society suffered or benefited from them? Many have also arrived, burgeoned and then declined. There used to be at least 5 amateur electronics magazines in the UK. All have now closed.

A niggle here. It is not dimensionally true to say you can subtract distance (or its square) from time (or its square). Time has dimension T The constant, c, has dimensions LT-1 When multiplied together the result has dimension, L

Interesting how Nature in the form of animal biology displays the reverse. Our muscles can only contract (pull), they cannot push. So muscular activity in our bodies is determined by the balance between two opposing muscles. Muscles work in pairs, pulling in opposite directions.

Sorry if I miscopied this but wonderful windows10 will again not let me copy and paste or use the quote function. Although his profile does not indicate much wtf posts as though he is or was a professional mathematician so it was good to see my words in post 3 echoed and much extended, in a particularly understandable and helpful way. +1 geordief, A really good place to look for this is the Cambridge University Text for SMP (school mathematics project) by E A Maxwell Geometry by Transformations This connects old and new style geometry and stirs in a little group and isometry theory rather well.

I believe my great great great great great grandfather's dog once mentioned something about angels and pinheads.

Usually the best way to test for conformity with the axioms is to concentrate on the operation. That entails knowing precisely what the elements are. You seem unclear as to what the elements of your proposed group are "I understand that Minkowski space is a group..." What elements are you proposing? Vectors? So what is the operation? (vector) multiplication ? Does the dot product produce another vector? Is there an inverse vector for this operation for every vector? Does the cross product produce another vector? Is there an inverse vector for this operation for every vector?

My comment was not a criticism or challenge, it was more to add information to the topic. That definition is consistent with a Physics view of randomness, which focuses on the route by which you get to the result, as opposed to the result itself. Mathematics (the Kolmogorov definition, which Wiki also discusses) focuses on the result and doesn't care how it is arrived at so answers my question Is 5 a random number? in the affirmative. We had a long thread a while back, that was before the current listing starts so I can't find, asking about the difference between random and chance. You will find precious few references to 'chance' in maths texts, but lots in Physics ones, because chance is about the route. There is a current thread here where 5 is defined as random. http://www.scienceforums.net/topic/97886-help-a-non-native-speaker-of-english-understand-this/

Take another look at group axioms. http://mathworld.wolfram.com/Group.html It is not necessary for a group to be commutative, only associative see axiom 2 in the link. The defined operation between the group members is called the group operation. This is part of the definition of the particular group in question, not an axiom. So we say multiplication over the real numbers forms a group. Such a statement specifies the elements and the operation. This operation must be between two elements of the group only and produce another member of the group. It is not necessary for the operation to be commutative; if it is the group is called abelian, but there are non commutative groups. Because it is between two elements it is called a binary operation (often it is called multiplication, but this depends upon what the elements are) Yes it has also been found most useful to require that the operation has an inverse and that there is an identity element. Note the the inverse and identity are both required, one will not do. Note that this is different from the definition of a vectors which requires two sets of elements, the set of vectors and the set of scalars.

A small point but what do you mean by random? Mathematicians and physicists operate on different interpretations of this word. So for instance is say the number 5 random?

It would be a real shame for several posters who have each contributed something worthwhile here to fall out with each other. For some English is not their first language and their posts are sometimes not quite what they meant as a result. We should all try to compensate for this. Here are two examples, at least one of which, may have lead to misunderstanding Obviously the word is pride not proud. but here a word is perhaps missing?? Did the poster really mean US citizens, usually poorly educated ones? bearing in mind that every country has well educated and poorly educated citizens.

There are many silicones, it is a class of compounds. It can be made as thick as grease or as an oil or thin enough to spray. As a sealant it can contain inert filler (there was a question here a few days aback about someone who wanted to do a thermogravimetric analysis) and be made sticky. The lubricants are usually non sticky. http://www.dowcorning.com/content/discover/discoverchem/si-lubricants.aspx

Nice and complete +1

Never heard of a WD40 version but sounds expensive, especially as they will not tell you the price. Knitmaster provided a can with my wife's knitting machine decades ago that we still use everywhere for a dry, non greasy lubricant. Curtain tracks, the window mechanisms, doors locks, things on the car....... It's like magic. We recently bought some unamed brand quite cheaply on _bay. Seems good.

Quantum theory presents its own mathematical difficulties to a block universe in the uncertainty principle, which is due to the non cummutativity of the operators. Incidentally this non commutativity is also present in some classical mechanics.

Just remember that acceleration is the second time derivative of distance and both quantities depend upon how you measure them. Oh! crossed with Mordred.

Silicone spray is good and easy, but will need renewing every couple of weeks or so on a bike chain.

I think we are both now agreed that the block universe has its merits, but also its shortcomings. Another one to consider is granularity. Relativity is a theory of continuum mechanics and continuous functions thereon. Quantum mechanics is the mechanics of a granular universe. It is not certain whether space and/or time are granular at some level.

Now you are thinking straight and asking sensible questions. +1

There is also no cause and no effect in such a four dimensional block, and therefore no determinism and no chance. Another way to put this is to observe that the relations between the points in such a block are not part of the block itself, but can be extracted from it or are external to it.

Yes I did end post#29 with that statement, but not quite with the meaning you inferred. I did not say that an external agent could not change one point or event (or even more than one). Indeed that whole argument was based on the proposition of an an external agent doing exactly that. What I was saying was that both chance and determinism refer to the relationship between at least two events or points. Therefore in a deterministic or chance or mixed universe there is a causal relationship between every point and at least one other point in that universe. So if one point only were changed then the relationship would become false. The block universe does not admit of relationships between points or events. Michel123456, I like your comments +1

Here is the back of my envelope for the unaided human eye. The receiving angle or angular field of view is 114o or 2 radians. Light travels at about 3 x 108 metres per second or 3 x 30 x108 metres in 30 seconds approx 1010 m So the arc of your max field of view is 1010 m. This is equal to [math]r\theta [/math] or the radius times the angle. The radius is of course the distance away of the travelling object. 2r = 1010 m r = 5 x 109 m or 5 million kilometers. Now if you will supply details of the illumination of the object, or if the object emits light in concentrated beams eg then the minimum size of object to supply the minimum eye sensitivity over this distance can be estimated.