studiot

Are you still interested in this?

I have an old Dell (Vista) laptop I'm using for controlling things in a play and am trying to get a handful of keys to play particular sound files on demand, without leaving the Powerpoint screen. Any ideas welcome. Already tried Intellitype, but can't seem to access the keys, let alone reprogram them.

Duplicate post with this one. Answers there. http://www.scienceforums.net/topic/97453-organic-chem-help/

+1

Modern solder for both plumbing and electrical work is lead free by regulations. Partial separation can be effected by physical means (heating) but the residue will approach the eutectic mixture ever more closely. http://www.chemguide.co.uk/physical/phaseeqia/snpb.html If you are able to heat to gaseous states and conduct fractional distillation this would work. Otherwise you will need to find an acid that dissolves tin but not lead (why not the other way round?) and follow this up with some chemistry. But all these are hazardous procedures, there is no easy way.

Since you didn't reply to my answer to your question which was basically where does the extra angular momentum/energy come from that is gained by the plane on its southwards journey, I hesitate to bother further. However think on this. The energy comes from the aircraft engine having to work harder. As others have said it will need to adopt a suitable heading to counter/keep up with the westward movement of the Earth's surface and fly at an air speed (did you look this up as suggested, there is plenty on BigG) which is greater than that of the southward progress. This greater speed will result in the engines working harder.

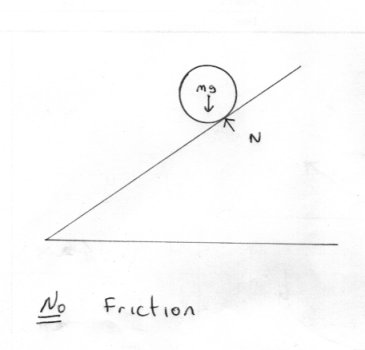
You gave two situations I started with the first and simplest. What causes the ball to roll if there is no friction? In the real world, air friction would be enough to turn it, but in our idealisation there are no such forces acting. Note that a vehicle or railway engine wheels will spin under the vehicle when driven from the centre axle without moving the vehicle if there is not enough friction.

Is this homework? You really need to explain the problem more completely otherwise people are left guessing what you mean. I am guessing that you are talking about a ball rolling down a slope from a standing start so the equation of constant acceleration applies with the downslope acceleration = gsin(x) so we have using vt = u + ft = 0 + gsin(x) * t Which is your first equation. But will the ball roll or slide down the slope?

swansont is correct, but perhaps to help you produce something closer to an appropriate analysis, here is a hint. Beginners often think that centripetal force is due to the circular motion and is somehow additional to the other forces that are acting. This is not so, it is the other way round, The circular motion is due to some force, in this case the one in the spring, and we call it the centripetal force. But this is the same force that is described by Hooke's Law, not an additional or different one. Does this help?

You are right to ask this as a classical physics question. Classically the plane is still subject to the Earth's gravity. Escape velocity is some 40 times as fast as your aircraft speed. It is also a good idea to revise the difference between air speed and ground speed, you seem to have blurred this distinction.

I know next to nothing about calcium acrylate chemistry, but there is clearly significant knowledge about. https://www.google.co.uk/search?q=calcium+acyrylate&rlz=1C1AVNG_enGB673GB673&oq=calcium+acyrylate&aqs=chrome..69i57.9069j0j8&sourceid=chrome&ie=UTF-8 I would hazard a guess that some intermediate reactions as with this TG analysis of calcium salicylate

You are testing a carbonate/polyacrylate mixture are you not I don't know what the decomposition temperature of the polyacrylate is but for silicone engine sealant it is around 300o C and you are testing much higher than this?

Where there's a will there's a whirl.

I find the quote system cantankerous at best but one tip I have discovered Write some text, any text you can always delete it later, before you invoke the quote function. You can then come back, at any time, and paste into the quotes at will.

To borrow a phrase "Be careful what you measure, It may come true!" When I was growing up there was a black and white TV programme called "Stranger than fiction" Later I worked in the Saudi desert where survey parties observed (measured) negative vertical angles at both ends of some observation lines. Reality was of course, somewhat different.

Rather than following a flippant treatment such as presented in your post#15 quote, I suggest you look up the following An angle modulated radio/light wave may not be sinusoidal, or expressible as a linear combination of them. What is the waveshape of light received from a body which is continually accelerating away? Solitons (solitary waves) as applied to (modern) optics. The difference between dispersion and dissipation as applied to waves. Gibbs phenomena in periodic functions.

Thank you for the positive and frank discussion so far. I have tried to encourage others (who have read this judging by the viewing numbers) to participate, not least the OP, moreno. I'm sorry you have limited your interest since I was preparing the next stage of my discussion, viz the transition from the 'little balls theory' to quantum theories. I will again post a few summary observations in case there is further interest. When we consider the bonding in alkenes we discus the pi bond and these carry over to polymer dienes. These pi bonds, which are formed as hybrids from the bonding atomic obitals have a definite shape and locality in space. This describes where we can expect to find the electron and where we can't. When we consider the same process in metallic bonds the bands that result are not like this and the band structure is not equivalent to a series of pipes through the lattice. In particular they exist in phase space, not xyz physical space. So the 'curvature' you describe exists on graph paper, not in real space, unlike the curvature of p orbitals and pi bonds. An electron in a band does not move about like a little ball but once it enters a particular band it can be anywhere within the range of that band. The electron acts a wave that spans the entire band but can only appear in one particular phase space sub orbital according to Pauli rules. I was preparing a comparative table of orbitals here are a few. We can discuss the implications if you wish. Note that Lithium Sodium, Potassium, Rubidium, Caesium, Copper, Sliver and Gold have a full shell plus an outer S orbital with a singleton electron. They all have 'normal' Hall coefficients. Beryllium, Cadmium, Tungsten and Zinc have 'anomalous' coefficients and have that outer S orbital fully occupied. Borderline cases, magnesium, indium and aluminium have the full S orbital, but also have a singleton outer p electron.

D is wrong because it looks at independent causative variables. The third variable is due to a variable common to both the measured ones.

Yes a selectional bias can create a false correlation, because the sample population may be drawn from only from those with the tested characteristic, by the selection process. Since this is homework help it is good to do more than just ask us to check you answer to boost marks. (you didn't do that did you?)

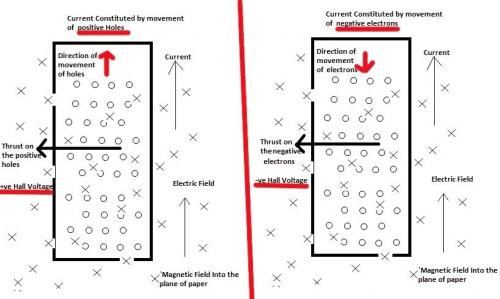
A few calculation and references to support your statements would be nice. Looking at my diagram here is something to ponder. We are discussing conductors and semiconductors, that is conductivity current as opposed to displacement current, not the special states that exist in superconductors. All conductors have some resistance (conductivity) and require an electric field to drive the current (even if small). Any explanation that states 'It's due to negative mass guv, honest' must also explain why the main current proceeds in the normal expected direction and only the hall current/deflection is reversed. Edit If you are going to offer the negative effective mass explanation, your explanation is insufficient, particularly if you wish to reject the deifinition I gave which is entirely conventional. Your statement is basically that of Dr Steve B here http://physics.stackexchange.com/questions/10800/how-can-the-hall-effect-ever-show-positive-charge-carriers Whilst I have great respect for Steve, his explanation was as lacking as yours as to why there should be 'curvature of the bands' or what that might mean or signify. There is something more fundamental going on that I was leading up to.

I haven't used any diagrams yet so here is one that I think is clear.

Most of what you have said in post#11 I agree with but this bit needs some thought. Not exactly. If hole movement was the same as electron movement then current could be described in terms of electrons only. But the holes and electrons are often in different bands. Anyway that does not explain negative effective mass. This is because mass is a non-negative isotropic scalar. Effective mass is much more complicated and is in fact a tensor. Effective mass in two or more dimensions can be positive or negative and vary in value. I don't know if either moreno or anyone else is still interested but I am going to start at a very basic level and expand some things normally just stated as granted in textbooks. So here is a gentle introduction to the implications of this. First let us consider speed and velocity as a simple example to set the scene. Speed is a non-negative isotropic scalar. A body travelling at a speed of V travels at V, whatever direction it is heading. Velocity is a vector. Velocity in two or more dimensions has positive or negative components that vary in value, depending upon the direction. So a velocity V due East has a component Vcos (45) in the North Easterly direction and -Vcos(45) in the South Westerly direction. And yet both speed and velocity have the same units or dimensions - metres per second or LT-1 Sometimes speed and velocity can be used interchangeably, sometimes they can't, as in the case of the calculation of momentum, which is always speed times mass, but you need to take all the velocity components into account if you calculate mass times velocity. Speed and velocity are generally well known and understood. Mass, reduced mass and effective mass less so. Especially as some authors in quantum theory call 'reduced mass' a form of effective mass and there are yet other definitions in other circumstances. So what definition of effective mass should we use in the Hall effect and what are the consequences? Well I will just outline the definition in this post and fill in derivation and detail later if anyone is interested. We define effective mass as the ratio of the square of Plank's constant to the second derivative of the particle's energy with respect to its De Broglie wave vector. [math]{\rm{EffectiveMass}}\quad {\rm{ = }}\quad {{\rm{m}}^*} = \quad \frac{{{{\left( \hbar \right)}^2}}}{{\left( {\frac{{{\partial ^2}E}}{{\partial {k^2}}}} \right)}}[/math] To see why it is called effective mass look at the units/dimensions. Energy has units Joules or L2MT-2 [math]{\left( \hbar \right)}[/math] has units Joule-seconds or L2MT-1 the wave vector, k has units: per metre or L-1 So the second differential has units energy per metre per metre or L2MT-2LL or L4MT-2 Putting this together with the square of the reduced Plank's constant we have [math]{\rm{Dimensions}}\;{\rm{of}}\;{\rm{effective}}\;{\rm{mass}}\;{\rm{are}}\quad \frac{{\left( {{L^2}M{T^{ - 1}}} \right)\left( {{L^2}M{T^{ - 1}}} \right)}}{{{L^4}M{T^{ - 2}}}} = M[/math] This has the same dimensions as the scalar inertial mass. So why is this a tensor? Well look at the bottom of the fraction. In the wave vector we have the cartesian product of two vectors, ie a tensor. Just like the simple example with a vector velocity the tensor has different components in different direction. These components are conditioned by the environment, not the electron but that is the subject of another post.

I see that you were online after I posted yesterday so presumably you saw my reply. I note also that you are a biologist, although you have posted this in the Chemistry section so I if you have any questions arising, don't hesitate to ask. Some further notes. If the temperature is not constant then you also have to integrate the SdT term. This can be performed at constant pressure. My analysis was for gases and the pressures are therefore partial pressures if there is more than one. Pressures are a measure of (molar) concentration and the reaction quotient or coefficient, q, can also be described in these terms, which is good for non gaseous components. You have used Q for the quotient, which is becoming common, when K used to be used. There is a danger of confusing the q used in the First Law with Q which is (partly) why K was originally chosen.

Hello Nikolai and welcome. Some questions for you to think about. If a moving electron creates a wave, where does the energy for the wave come from? Does the electron loose energy as a result? Can this be measured? (Look up Bremsstralung https://en.wikipedia.org/wiki/Bremsstrahlung ) If the wave is 'extinguished', where does that energy go to?

This is an important question so I am going to work through it at some length. It is important to distinguish between the various Gs and G0 s and their deltas. G on its own refers to the Gibbs Free Energy function, which is a function of state. G0 is just the constant of integration, and is made specific to each reactant and reaction by choosing a stated condition. The integration is not of ΔG = ΔH - TΔS as you thought but of either Maxwell's relation [math]{\left( {\frac{{\partial G}}{{\partial P}}} \right)_T}[/math] Which brings out the fact that this is developed for gaseous reactants at constant temperature or of the equation [math]dG = VdP - SdT[/math] Since T is constant, SdT = 0 and we are left with the following [math]{G_T} = \int {Vdp = nRT\int {\frac{{dP}}{P}} } = nRT{\log _e}\left( P \right) + {\rm{constant}}[/math] The state function of temperature has a value at any T given by integrating the above Working per mole n = 1 and we set the constant equal to G0 Thus [math]{\rm{Constant}} = {G^0}[/math] and [math]G = RTLo{g_e}\left( P \right) + {G^0}[/math] This is the general thermodynamic equation. To apply it to a particular chemical reaction say [math]A + B \to C + D[/math] we calculate the change in G as ΔG by summing the values for the reactants products and subtracting the values for the products reactants Edit oops ! [math]\Delta G = {G_C} + {G_D} - {G_A} - {G_B}[/math] Each of these four components individually follows the general law so substituting this in [math]\Delta G = \left( {RTLo{g_e}\left( {{P_C}} \right) + G_C^0} \right) + \left( {RTLo{g_e}\left( {{P_D}} \right) + G_D^0} \right) - \left( {RTLo{g_e}\left( {{P_A}} \right) + G_A^0} \right) - \left( {RTLo{g_e}\left( {{P_B}} \right) + G_B^0} \right)[/math] Collecting terms and rearranging [math]\Delta G = \left( {G_C^0 + G_D^0 - G_A^0 - G_B^0} \right) + \left( {RTLo{g_e}\left( {{P_C}} \right) + RTLo{g_e}\left( {{P_D}} \right) - RTLo{g_e}\left( {{P_A}} \right) - RTLo{g_e}\left( {{P_B}} \right)} \right)[/math] This shows the various reactant and product contributions to [math]\Delta {G^0}[/math] in the first bracket Doing some algebra on the logs yields [math]\Delta G = \Delta {G^0} + \left( {RTLo{g_e}\left( {\frac{{{P_C}{P_D}}}{{{P_A}{P_B}}}} \right)} \right)[/math] Defining the reaction coefficient, Q as [math]Q = \left( {\frac{{{P_C}{P_D}}}{{{P_A}{P_B}}}} \right)[/math] and substitution yields [math]\Delta G = \Delta {G^0} + RTLo{g_e}\left( Q \right)[/math] Which is your equation for this particular reaction. Remember always that G on its own is general, but introducing G0 makes it specific to a particular reaction.