studiot

Perhaps you don't understand plain English. You clearly misinterpreted what I said because at no point in my life have I ever claimed that a free electron is an orbital, or even connected to one, even when I was at school. I actually asked a question because you claimed congruence between electrons and orbitals and I asked question 3 because I wanted you to demonstate this claimed congruence for a free electron. You cannot have it both ways. Either an electron is an orbital or it is not. Which are you claiming? You have been very fond of telling me that I'm wrong on this forum, yet I did not initially flatly contradict you. Rather I offered you the opportunity to think again by expressing doubts and requesting more details, indicating the areas of my doubts. Your response was a direct personal attack, which has continued in that vein since.

A lump on one side of the washing machine huh? There is one place in a washing machine the washing stays away from. The axis of rotation. This represents a fundamental difference from the Earth's continents. Pangea was not the first super continent, nor is it likely to be the last. But look at today's globe. The continents are lumped together, not equatorially or on one side of a spinning globe, but spread around the axis concentrated close to the poles. http://www.nature.com/nature/journal/v482/n7384/abs/nature10800.html

OK I will start the ball rolling. First the word abscissa refers to plots of specific points on 2D planar graph paper. It is the coordinate relative one of the two sets of gridlines, by convention the horizontal gridlines on the graph paper. The other coordinates are called ordinates. By convention these are relative to the vertical gridlines on the graph paper. Now for the 'curvature' of spacetime. This depends upon your point of view. Here is an analogy, due to John Baez, a noted californian physicist. Two men stand at the equator and look directly at each other. They both mark off a right angle from the equator towards the North and start walking, both keeping straight on due North. That is as far as each can tell they are each walking in a straight line and they check this by checking the perpendicularity as they cross each parallel of latitude. As they approach the pole they realise that they are coming closer and closer together, although both are walking along a gridline perpendicular to their startline. So what is happening? Explanation 1) There is a mutual attraction, a sort of personal gravitational force drawing them together. Explanation 2) They are somehow not wallking in a straight line but a curved one. Now this example is not yet into spacetime, it is simply 3D space. But it is sufficient to explain quite a few things. The men are confined to a 2D world, the surface of the Earth. We call this a manifold. The manifold is simply all the places (points) accessible or available to the men. From the point of view of an outsider the surface (manifold) is curved in 3D so the gridlines of longitude converge. Further they are not straight but curved. So the outsider goes for explanation 2 From the point of view of the men, who cannot (let us say for the purpose of this exercise) see 3D, they cannot see this curvature So the men feel justified in going for explanation 1. There we have two explanations, a curved manifold or gravity in our model. But there is a further twist. The men have a choice. They could carry on with their coordinate system of lines of latitude and longitude, completely within the manifold. Or they could postulate the existence of curvature in a third dimension and draw up an X, Y, Z coordinate system. Then their paths become space curves (arc of circles) and they could call them geodesics. Projecting this forward to 4D spacetime we can do the same thing.

Everyone deserves the right of reply. But not to call the other persons statement nonsense. Particularly when you specifically said "The orbital IS the waveform of the electron", emphasising the word 'is'. Now some electrons are free. So I asked you to describe the obital that is the electron, in this condition.

An empty orbital has more in common with an empty bookshelf. Whilst the book is on the shelf it is on a ledge in a potential energy field. If I remove the book does the shelf disappear? But as swansont has pointed out there is more to quantum orbitals than just energy levels so they are more complicated than bookshelves.

DrP, you should not imagine the comparison with your guitar string. Orbitals as solutions to the Schrodinger equation only bears a passing resemblence to the solution to classical wave equation which your cuitar string obeys. If you twang the string you can see a shape in space describing the vibrations. If you are inhumanly very very quick you can catch the string at the top of its vibration between your fingers. At this time ther is no possibility that the string will elude your grasp simply because it is at the opposite side of its vibration. That is what you see is a time averaged blur comprising mostly empty space. The orbital is not like that. Wherever you 'grab' it you will have some interaction with any electron in that orbital, as any atom approaching to bond will experience. The electron is not on one side of the vibration at one time and on the other side at another as the string is.

Wow, that is rather peremptory. Did I offend you? To answer your comments in reverse order 4) So you are saying that if I remove 1 electron from the 1s orbital of Helium, the orbital I took it from collapses? So what happens to the other electron in the 1s orbital? 3) So is this a claim that a 'free, unbound' electron no longer obeys quantum mechanics in general and the wave equation in particular? 2) So how do you explain bonding orbitals and anti-bonding orbitals? 1) So what? well this is tied in with question 4, already answered.

Not convinced. 1) An orbital can contain more than one electron, 2) What are you suggesting empty orbitals to be? 3) Please describe the 'orbital' of a free electron. 4) If an electron becomes free, ie leaves an orbital, what is left behind? Does the electron leave part of itself behind?

The whole point of this thread appears to be that you wish to demonstrate the truth of its title. Unfortunately the title is imprecise since it employs imprecise words such as reality and existence. Existence in particular has a specific meaning in mathematics, which does not directly correlate with our ideas of reality, physical or otherwise. But you also asked a specific question of a mathematical nature, which seemed to me to question whether infinity could be handled mathematically and I gave a specific answer. My answer, as does your reply quoted above, showed that it most definitely can. So if you want to you can handle very large numbers or infinity mathematically. We are agreed.

If a number is large but not transfinite it will follow the rules for finite numbers, however big it might be. So , for instance, given any integer, however large, I can easily make an even number from it (guaranteed). If the number is transfinite then you can follow one of the schemes of rules for the manipulation of such numbers. There is more than one available and they are all different from the schemes for the manipulation of finite numbers.

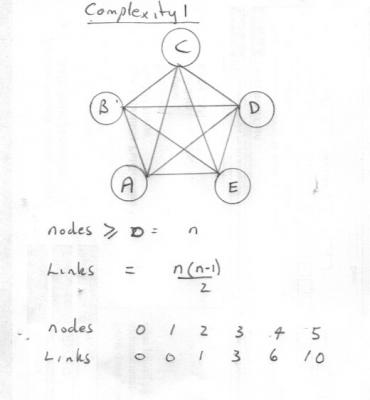
In order to put some flesh on the bones of my question here is an introduction to infinite and complexity for discussion Infinite We say an infinite something. But what? Consider the following two lists (sequences in maths) 1, 2, 3, 4.................. tan (0), tan (15), tan (30), tan (45), tan (60), tan (90) The first list is an infinite list of positive integers. That is is does not terminate or goes on forever. The list has no end. So we say it is an infinite list or sequence. But every one of the integers on that list has finite magnitude, ther are no infinite 'numbers' on the list. The second list terminates or contains a finite number of items. So it is not an infinite list. Yet one of the items on the list has infinite mgnitude. This is what I mean when I say that we have to be clear what we are applying the adjective infinite to when use it. As above some properties may be infinite, whilst some may remain finite. Complexity. This is a noun and again it can be taken in more than one way. Here is one interpretation, that can lead to a concept of infinite complexity, along the lines of the first example above ie it never ends. Consider a list of items, such as facts, theorems, properties etc. Call these items A, B, C, D, E etc Now these items may be linked by connections of some sort, eg equations or whatever. The totality of all the connections can be regarded as a measure of the 'complexity' of the system. The following diagram shows the maximum number of single links for 5 items, where every item is linked once to every other item by connections shown as lines. A formula and list for other numbers of items is also shown. You can see that in this model the system comprises the items and the links and the complexity is given by a simple formula such that the complexity remains finite so long as the number of items remains finite. However the complexity becomes infinite for an infinite number of items. Does this help the discussion?

I don't know, but I do know that I made a genuine offer to rationally discuss the terms you used, by asking my question in post#25 to which you have not responded. It is against the rules of this forum to ignore polite questions in this manner.

Whilst you deserve acknowledgment for adding the important word 'might', you still have not explained what you mean by complexity. This is important because infinite is an adjective that has at least a couple of meanings, but it has to have something understood to be applied to. So what is your explanation of complexity and what about this explanation can the word infinite be correctly applied to?

This example brings up another point for down the track. The pentagon is a closed shape, called a ring or cyclic structure for obvious reasons, however it is not the most common or important one. You should always be aware which ring you mean, it is particularly, if your glance is too quick you can confuse the pentagon and hexagon. The hexagonal benzene ring is the most common arrangement and the basis for a large branch of organic chemistry, the aromatic compounds. http://www.2b1stconsulting.com/benzene/

Well we should be well protected since all our mods are now godesses.

A walks towards B. But B is walking towards C who is walking towards....... etc So A is constantly turning inwards as he is always walking directly towards B. Draw a sketch and you will see what i mean.

Foxy has a point. This reminds me of the following question. Four circus performing fleas are placed at each corner of a 1 inch square ABCD. At the ringmaster's whisltle all the fleas start to walk towards their neighbour. So A walks towards B, who walks towards C who walks towards D, who walks towards A. They all walk straight towards their target at all times. Since they are all in motion each flea walks a spiral path and they meet in the centre. How far does each flea walk?

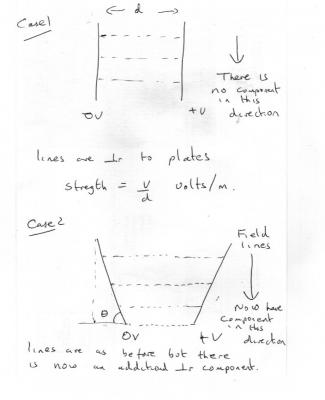
In all cases the field strength equal the voltage divided by the plate separation E = V/d But in the second case the plate separation varies, due to the geometry so this induces a second component, perpendicular to the original, as the field strength increases from bottom to top, as in the diagram. This causes the electron's path to curve. Is this really an A level question?

1) What do you think the path of the electron will be in both cases? 2) sketch the lines of constant field strength in both cases. 3) What is the angle between the constant field strength contours and the Force on the electron. 4) What do you think this does to the path of the electron?

Thank you. A single hydrogen atom has one electron. So this is the only case in which the issue of which electron does not arise. swansont's replies show that even here the possibilities are beginning to get complicated, and I am struggling a little bit to find a level to answer. So here goes, here is the simplest answer I can think of. Moving the electron to a higher energy level moves it further out from the attracting positive nucleus. So electrostatic attraction will pull it back in, if at all possible. This is similar to saying that if you throw a stone up, gravity will pull it back down to Earth. Also similar to gravity, where if you (or the HULK) throws it up hard enough the stone can leave the Earth entirely, it is possible to remove that electron and take it away somewhere so that it will never fall back o its original state. That is what I meant by the environment and the process of excitation. Not important in single hydrogen atoms, but very important in thermionic emission or conduction bands in semiconductors or conductors.

Several things need amplification here. First and foremost the energy state belongs to the environment of the electron, not to the electron itself. Secondly the above quickly glosses over the means by which the excitation occurs. Thirdly it may not be that specific electron that 'falls back' to the lower state. So please tell us more about the context of the question. Is the electron in an atom, a molecule, a metal, free space or what before excitation? Secondly what method of promotion are we discussing, light, heat, electric field or what?

The commonly called Principle of Equivalence boild down to an assertion that the m in inertial equations, such as Newtons 2nd Law, is the same as the m in gravitational laws (Newtons included). This has been repeated demonstrated experimentally to ever greater levels of precision. Eotvos experiments confirmed it in Einstein's day. The principle has often been quoted as its logical consequence or deduction viz that a blindfolded observer cannot tell the source of a hidden acceleration she experiences.

Do electrons collide?

Fine, look out for the next post about entropy and surface energy. BTW what are you studying? You originally said this came up in Chemistry, so I have been trying to put things from a Chemistry point of view.

Noonespecial, Please note, I am not saying everything you say is wrong. Far from it. But I am saying it is only part of the whole story, as with my example of area or ajb's ones from mechanics. But you are practising what mathematicians (and other scientists) often do. Limiting the scope of your domain of discussion to achieve internal self consistency. This is fine so long as you acknowledge these limits and do not try to apply the results outside their scope. Much misunderstanding arises from failure to do this. Now we have (hopefully) agreed that multiplication can lead to new things outside the scope of your definitions, let us revisit addition. What is 10 plus 7? but It is 10 o'clock. What is the time if I add 7 hours? The recipe for a cake reads "Add two eggs to the dry ingredients." What do I have if I add two spoonsfull of sugar to my cup of tea? What do I have if I add oil to water? Chemical safety instructions read "Always add acid to water, never water to acid" One of the properties of addition to explore in the above is What happens if I switch the quantities being added That is is (a + b) the same as (b + a) We often want this in mathematics and often phrase our rules to force this. But you can see that in the real world this is not always the case. Now interestingly consider the same question for subtraction That is is (a - b) the same as (b - a) If you really want discussion, not a platform, the above are some points of discussion about your material for you to respond to.