-
Posts
18475 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
Answer to both, Yes, of course, but the wall velocity remains at zero and the force developed is rate of change of momentum. Edit Remember also that a speeding solid body (meteor) striking a (relatively) stationary fluid is the same as a speeding fluid striking a (relatively) stationary solid body (wall).
-

What's the "definition" for this law?
studiot replied to Elite Engineer's topic in Classical Physics
Can I come to you for spelling lessons, endy? Thanks. +1 -
Well I started this thread to share information about something that will affect most over the coming years. So here is my latest installment. Last week I was called to fix a failed accounts PC in a small aerospace manufacturing company. We agreed the best solution was to replace and discussed with Sage and HMRC about the virtues of W7 v W10. We were assured that the Accounts, Payroll and Tax packages would run happily on W10 so we should go for this. Naturally we needed the pro or business version and like many businesses had been waiting for this to appear. Now we deal with the largest trade supplier of electrical and electronic equipment and components in Europe and I had just received the February 2016 update to their current 4000 page catalogue. Great, I thought, A new range of lenovo W10 business machines, ready to go with W10 loaded. Better a range of W10 installation disks for sale! Better yet, 5 in stock. So I ordered one, with intention of getting the rest if it proved satisfactory. Roll on this Monday (didn't Abba write a song about this?) When I went to install the new machine, guess what. Yup still W7 in the box, although it was labelled W10 and had a W10 licence. No it was not a mistake, The supplier's Technical Director said "We only move boxes, We are not responsible for what is in them" And the installation disks. Well they are just figments decorating the catalogue pages.
-

What's the "definition" for this law?
studiot replied to Elite Engineer's topic in Classical Physics
Actually it does. The mechanical device similar to using the blunt end is called a (cone) penetrometer and is used in to asses the bearing capacity of soil. https://www.google.co.uk/#q=cone+penetrometer This measures the pressure applied and resisted. Pressure is a direct stress, not a shear stress and does not lead to rending division of the material, as does shear stress. The sharp end of a tool causes rending, not squashing. -
Hi, Pavel. Firstly be careful talking about a wave. Waves have no net momentum to transfer. You mean a pulse. Secondly as the meteor traverses the atmosphere it exerts a ffrictional force on the atmosphere (and the atmosphere on it) . This force appears as a result of the destruction of its linear momentum in that direction. This is similar to the destruction of forward momentum when a liquid jet impacts upon a wall. The science of momentum transfer and exchange (in this context) is called transport phenomenon and the classic text is Transport Phenomenon Bird, Stewart and Lightfoot IMHO it is one of the best textbooks ever written on any technical subject.
-

What's the "definition" for this law?
studiot replied to Elite Engineer's topic in Classical Physics
The theory of using sharp edges or points to cut materials is dealt with in mechanical or industrial tooling engineering under the title 'metal cutting principles' In general cutting action involves shear forces, which why you need to get the correct angles for cutting different materials. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=metal+cutting+principles&gbv=2&oq=metal+cutting+principles&gs_l=heirloom-hp.3..0l6.922.6016.0.6438.24.15.0.9.9.0.219.1767.1j11j1.13.0....0...1ac.1.34.heirloom-hp..2.22.2032.HQz2oHwvGKE -

Geodesics, free fall and the equivalence principle - for dummies.
studiot replied to Robittybob1's topic in Relativity
I thought I provided a recap? How about you tell us your understanding of what a geodesic is? Perhaps I can learn something. -

How to know the variable dependencies of the solution of a PDE?
studiot replied to torstein's topic in Mathematics
Solving such equation generates surfaces over which we sum the flux variable and apply continuity. The flux is obviously sensitive to the area of this surface. So for instance with a cylinder the area depends upon z (the axis) that is how long the cylinder is. It must also depend upon r the radius. But for a complete cylinder the flux is constant we just sum over 0 to 2pi and equate to the source strength. -

Geodesics, free fall and the equivalence principle - for dummies.
studiot replied to Robittybob1's topic in Relativity
Geodesics, free fall and the equivalence principle - for dummies. Perhaps it would be easier to understand if you separated the disciplines, Mathematics and Physics (Mechanics). The study of geodesics is very firmly set in the realms of Geometry and the latter concepts in Physics. I’m sure Mordred knows considerably more of this Physics than I so I will leave that side to him. After tallying, geometry was the earliest form of mathematics and developed to a high standard well before algebra. Geodesics were known semi precisely to the ancients. More modern detail came with the development of cartography and surveying following the rennaissance; Newton actually wrote about the motion of a body “In its right line”, a clear reference to the ancient definition of a geodesic. From Gauss to the late Victorians, the subject developed, with applications in manufacturing in naval architecture, sheet metal working, later extended to paper and cardboard working. The idea of a geodesic as a particular path through space or on a surface was formalised and the ruled surface much studied in industry. Differential Geometry was introduced as a subject, followed by non linear geometry and new more esoteric geodesics were studied. In my opinion, the best way to study geodesics for understanding in a modern setting is to start with the simple classical geodesics on a sphere and cylinder. Then move on to look at geodesics on a geoid. Then introduce a modern manifold (which the surfaces of spheres, cylinders and geoids are). This route leads to better analogies than the usual picture of a ball on a trampoline (and explains that one too). We can follow this route if you are interested. -

Does anyone have an idea of the origins of this object?
studiot replied to pmer27's topic in Earth Science
A piece of NY basalt from here ? https://en.wikipedia.org/wiki/The_Palisades_(Hudson_River) Are there any quarries with crushers in the area? -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
No, I'm sorry, it is you who is missing my point. Of course later knowledge will, in general, take us further. That is the nature of progress. However later knowledge may add to, replace or disprove existing knowledge. I gained the distinct impression you were only considering the last mentioned case. I have been the only poster with a nose above the parapet offering something (in Physics as requested) that may never be proved incorrect. Can we please discuss that without the steamroller effect? -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
With all due respect, I think that is like throwing the bathwater out with the baby. Just because there is a new baby it doesn't necessarily invalidate the bathwater. There was indeed a time, before negative numbers, where the equation x + 3 = 0 had no solution. But the introduction of negative numbers did not invalidate the known solution to x - 3 = 0. -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
I wouldn't know but I can tell you that The Sausage Conjecture has been tested beyond 42 dimensions and found to hold true, although it does not hold true at some lower dimensions. Reference Conjecture : Toth Most recent test Betke, Henk and Wills -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
How does that apply to the triangle inequality and the Physical laws that flow from it? -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
Yes the Physics definition seems as good as any, though don't expect 'general' to be too general. It fits both Fermat's and Huygens Principles. You don't seem to have noticed I gave an example of a bunch of Physics 'Laws' (I am not going to write the rest of the list out every time) that appear to be unbreakable. In the micro quantum world Heisenberg's UP and in the macro electronics world Nyquist and the minimum bandwidth theorem all come from the same stable as the triangle inequality. -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
Although it can be expressed more accurately using mathematics. Thank you Strange, forgot my own thoughts there, I meant Huygen's Principle of course. Fermat's is indeed mathematical, but nevertheless a good example. -

Are there Universal Laws? Can you break them?
studiot replied to Robittybob1's topic in General Philosophy
Violating the triangle inequality would require some rewriting of mathematics, greatly affecting the parts of Physics that depend upon it. Which brings us to an issue that has been touched on, the difference between a Law, a Theory and I will add one more, a Principle. Although there is a Principle of Relativity, here is a simpler example. The Principle of the Lever is semi mathematical in that it comes in the form of an inequality, The Law of the Lever is fully mathematical and comes as an equation. Fermat's Principle, on the other hand is non mathematical. -

some questions about graphing equations and expressions ??
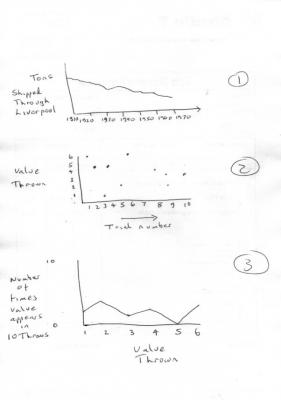
studiot replied to bimbo36's topic in Mathematics
That would be true if all of mathematics was deterministic. But folks so often forget that statistics is part of mathematics. Here are three graphs in statistics. You will always get the same graph for the first one since it is simply a historical record of tonnage shipped through the port of Liverpool in the first half of the 20th century. But the next two wil produce many different graphs as they record a random variable. I hope this was helpful in your quest, though I am not quire sure exactly what you are looking for. -

some questions about graphing equations and expressions ??
studiot replied to bimbo36's topic in Mathematics
Thanks for the cool vids in post #2. +1 Here is a graph question to think about: When you draw a graph will you always get the same graph for the same expression? -
First gravity v epicycles. Gravity is big, fundamental and long range. Epicycles were a small correction to a big fundamental theory to explain small perturbations. the main geocentric theory of the celestial sphere otherwise worked quite well. So they are quite different. Perhaps the caloric theory would be a better example? Perhaps, though that is debatable. However can Science not determine that which is definitely untrue / unreal? Did not new and better data allow us to move on from the geocentric theory to more modern and better theories, heliocentrism being the subsequent step, but not the last or latest. I think we are all saying (Simon included) that Science moves on in the light of better data. Please remember that, as swansont has hinted, what you understand 'bending' to mean and what GR means are also quite different. I attribute that to the popular analogy of the 2D surface of a 3D sphere. The analogy is poor to put it mildly
-
So what? So the theory of fluids regards hydraulic fluid as incompressible when you are designing a braking system, but compressible when you are measuring the displacemment of the piston to micrometres. So if you are designing an antenna to pick up radio Denver then your EM wave theory is more than adequate, but if you want to discuss Bremstralung then perhaps QED is the better option. It's horses for courses mate.
-

Base 256 character set, and "Base Byte" numbering system.
studiot replied to tar's topic in Mathematics
Gosh was it so long ago? Here is some tech data from a textbook in 1983. Note that the matrix is two bytes or 16 bits high and 7 bits wide. Whtever, the characters you can use are determined by the fine dot matrix of the 'character generator' chip in the electronics. The example shows upper and lower case P I am not up with the latest chips but the principle remains. -
Here you go The bible http://www.amazon.co.uk/Underwater-Acoustic-Positioning-Systems-Milne/dp/0419121005/ref=sr_1_1?s=books&ie=UTF8&qid=1455642872&sr=1-1&keywords=underwater+positioning+systems and a useful e-paperback http://www.amazon.co.uk/Acoustic-Network-Underwater-Positioning-System-ebook/dp/B007QF5IZO/ref=sr_1_2?s=books&ie=UTF8&qid=1455642872&sr=1-2&keywords=underwater+positioning+systems
-
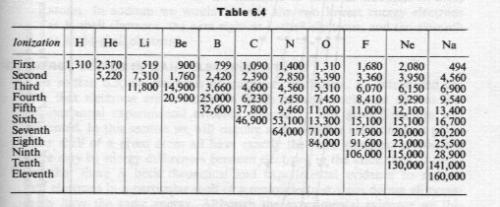
Lets do shells first. Here is a table of ionisation energies in kJ/mol. (after Stranks et al) This is a table of the energy to successively remove electrons from atoms. Look first at Sodium at the right hand end of the table. Sodium has eleven electrons. The first electron is comparatively easy to remove. The second electron takes about 8 times as much energy to remove. The increase for the next seven electrons `is relatively modest. There is again a big jump to remove the last two electrons, but a small difference between them. This pattern is repeated in the other atoms listed, as far as they have electrons. Now if we assume that how tightly bound an electron is (as measured by the energy to remove it) depends upon its distance from the nucleus we can see three distinct groupings of electrons, diminishing with distance. We call these shells and give them a number, n (1,2,3) or a letter (K,L,M) Because we number outwards from the nucleus the K shell = shell 1 corresponds to the closest and highest energy and therefore last two ionisation energies in the table. There are two electrons in this shell, eight in the next and one in the last. If this is helpful we can go on to the connection to orbitals.
-
I have to say I'm puzzled by these posts. The first one makes no sense. The second add nothing by way of explanation or the reason for either in this thread. As regards the scientific method, its purpose is simple. We can create many theoretical constructs, the scientific method is there to enable us to establish which one in fact holds sway. That is it is there to sort the sheep from the goats.