-
Posts
18270 -
Joined
-
Last visited
-
Days Won
104
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
That's why I look forward to the day when we know everything.
-
Excellent attitude +1 Ruthless Optimism If you count James Clerk Maxwell as being the start of modern descriptions of electric effects, then only two centuries My point (although it was rather obliquely and gently put) was simply to observe that you wrongly attributed electric field theory to Newton. Roping something he didn't do in with something he did devalues your argument about the correct stuff. I agree with that this effect has sadly occurred many times in scientific history. However I regard this as a separate process from thinking outside the box. The new thinking may destroy the box or it may strengthen and extend it. 'Paradigm shift' is certainly not a prerequisite, a new trick for an old dog would suffice to classify the thinking as outside the box. Then there is the issue of timescale. (Some of this is really directed at Strange and others) It is easy to say in hindsight that the conventional establishment was right because the white hats prevailed in the end or 'we now know that A's new thinking was right and have replaced B's theory with it.' But can we really claim that as an establishment victory if B holds back A during their lifetimes and the establishment continues with B's theory until C comesalong and proves A's. Here is a real world example. We now regard Cantor as one of the founding geniuses of modern mathematics, But look at this short history, ringed in the attachment.
-
What you have found is the Shockley Equation for the dynamic (ac) resistance of the junction. The Schockley equation says the dynamic resistance = 25mv/IE. Since there is no ac signal we want the static or dc resistance. I will dig out a 2N3904 tomorrow and post some real measurements (not SPICE sims that will depend on the model and is probably outside the range of the formulae)
-

Learning calendar / Action plan / ghantt chart
studiot replied to DevilSolution's topic in Suggestions, Comments and Support
One problem applying any sort of management control chart to learning is that of critical mass (of knowledge) required to achieve any particular stage. Learning is a spiral process or recursive whereby we visit several, even many areas or aspects of our subject at a particular level, using the knowledge gained from the previous cycle and generating new knowledge to base the next cycle on. You can't, for instance, learn how to calculate the area of a general triangle until you have learnt some geometry, some algebra, some coordinate geometry and or some trigonometry. Management control charts are useful in learning for controlling assignments, but a simple calendar often suffices for this. -
Well if my explanation wasn't enough, perhaps you would be good enough to say why?
-
Easy bro, there's oles and then there's ole's. If you have a bar of absolutely pure silicon and remove an electron toy have a positively charge ole and the bar has a net positive charge. If you have a bar of silicon doped with one atom of boron, you have an ole' but the bar remains electrically neutral. Sorry my Spanish is not really that good.
-
Indeed there will be a small leakage, which is why I pointed out that the 2N3904 is a modern transistor. By modern I mean it was introduced after we learned to make near ideal small signal transistors. My tables give the leakage at less than 15 nanoamps. Now the intrinsic emitter resistance is less than 100 ohms so the voltage developed by this mechanism, iw 15nA passing through 100 ohms is 15 x10-9 x 102 = 1.5 microvolts.
-
You are welcome to explain your thoughts and propose a mechanism.
-
RuthlessOptimism, I'm sure communication would proceed much more smoothly if you toned down your tendency to hyperbole and all embracing declarations in support of your points, some of which are quite good. This is the declaration I took issue with, the word every being highlighted. Had you used the word some I could have agreed. I see that Strange has noted the same effect. I can't agree with your latest claims, again hyperbolem with a counterproductive affect. Just how many centuries before any modern exposition of electric effect was Newton? Finally you are entitled to your opinion but I think most people would place the discovery of the fire, the molecule and antibiotics were extremely significant landmarks in the history of Science. Those examples were chosen to represent a whole class of advances/discoveries that had no antecedent theory (the box) to negate and therefore cannot be said to have destroyed any previous theory, popular or otherwise.
-

Cardinality of the set of binary-expressed real numbers
studiot replied to pengkuan's topic in Mathematics
Why can't they have infinitely many digits? Incidentally the conventional way to state this is to say they neither repeat nor terminate. It avoids the use to the term infinity. -
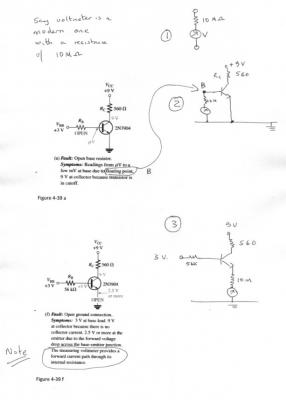
With reference to my attachment showing comments. A modern voltmeter for this purpose is likely to have an input around 10 megohms. This is in series with the meter. I have shown this in my fig1. My fig2 shows how this voltmeter is connected in your circuit 4-39a and identifies the floating voltage pont B at the base of the transistor. If you look at my version you can see that the base is not connected to any voltage but is earthed (connected to zero volts) through the 10M of the voltmeter. In theory the voltage at the base is indeterminate since it is not connected to anything. (In theory it is totally isolated from the base and emitter by the internal structure of the transistor. In practice the leads and internal circuitry of the voltmeter form a crude antenna which picks up stray (mostly radio) voltages across its terminals. You can see this effect on the voltmeter by simply turning it onto a low micro or millivolt range and watching the random readings. As soon as the voltmeter is connected into a complete circuit this effect will disappear or be swamped by the usual action of the live circuit. However in the connection shown it is not connected to a complete circuit since the base is not connected to anything, except the transistor base. One of the voltmeter's terminals is tied to earth, so the random pickup voltage will appear at the other one ie the one connected to the transistor base, thus varying the apparent voltage at the base. Note this voltage is only likely to be present when the voltmeter is connected since the base leads and circuit board pads are short. My fig3 shows the voltmeter connected to read the open emitter voltage as in your fig 4-39f Here we have a different situation since with the voltmeter connected the transistor has full connectivity, albeit through an excessively large emitter resistor. This 10M emitter resistor restricts the collector current to slightly under 1 microamp, bu that is enough to almost turn on the transistor as we see that the base is at 3 volts and the emitter at 2.5 volts + , just slight under the normal 0.6 to 0.7 base emitter voltage for a correctly biased 2N3904 in the active region. I have noted that the book explanation says this rather more briefly.
-

Is logic a branch of philosophy or maths?
studiot replied to andrewcellini's topic in General Philosophy
Please don't close it yet. I am still waiting for next week's lotto numbers. -
More than 100 views over the 1000 on this thread, yet no one else seems to have anything to say? I am sorry you could not locate the books locally, part of the reason I mentioned them is that they readily are availble secondhand at reasonable prices from international online supplies such as abe. I would council against avoiding examples until the end. Numerical mathematics is an enormous subject and trying to learn all the theory before application is about the most difficult way I can imagine. The example I offered take no more than 5 minutes and the back of a small envelope to figure out. But it does provided the opportunity to discuss many of the principles underlying numerical techniques without difficult numbers getting in the way. Incidentally it is always a good idea to try out a technique on a known easy example. The posh word for this is calibration and is one of the subject areas missing from your list. Talking of lists, yours seems largely to be a list of methods or techniques and I have to tell you that it is far from complete. The old fashioned (I called it standard before) presentation of numerical methods was just this an ever growing list of methods and techniques. An alternative is to divide into subject areas, here is the contents page from the book by Brebbia "Computational Methods of Solution of Engineering Problems". You will note that almost nothing here is on your list. Yet even Brebbia's list is far from complete. Some further subject areas include Optimisation Maximum and Minimum problems Variational methods. Numerical transform methods Numerical Harmonic analysis Potential Theory Exploiting the link between boundary and body elements using numerical versions of Green's and Gauss' theorems, Linear programming Non linear programming Computational Efficiency and Accuracy and Error Theory. Here is another problem for an accountant to ponder.
-

Cardinality of the set of binary-expressed real numbers
studiot replied to pengkuan's topic in Mathematics
To answer this you need to go back to your definition of countable and countably infinite. -
Why do you guys have to have such long handles to type in? I can't agree with this. Since you like lists here are a few major discoveries/breakthroughs that were not borne in such strife. Ut pendet continuum flexile, sic stabit contiguum rigidum inversum The discovery of penecillin The discovery of the vulcanisation of rubber Probably the discovery of how to make fire Your stout defence of the good name of scientists in general is fine but sadly misplaced in certain individual cases. Berzelius suppressed the development of Chemistry for at least half a century. The denial of Bayesian statistics by Pearson and Fisher and its resulting suppression for nearly a century.
-

Cardinality of the set of binary-expressed real numbers
studiot replied to pengkuan's topic in Mathematics
One thing to remember in what you are attempting is the difference between fractions and rational numbers. A fraction, say 2/3 is different from the fraction 40/60. In fact there are infinitely many fractions with that same value. But they all represent the same rational number, because the rational number is an equivalence relation that forms a proper partition of the set, indifidual fractions are not. I have not studied the effect of this in binary (or any other base for that matter), but I am sure it will be present. -
Thank you phi for researching the origin and history of the phrase, that is all new to me. It would seem that there are those who find its use distasteful and those who consider it a badge of honour. There is therefore an obvious potential for misunderstanding its usage. As a child of the 50s and 60s I would place myself in the badge of honour camp; it is the only version I have ever known. I have always thought of the usage to be particularly for situations when there would normally be a conventional solution but some additional (new) constraint is acting to prevent or obstruct success. These constraints may be financial, physical, artificial or whatever. This interpretation would exclude genuine new inventions or discoveries. I think perhaps 'blue sky thinking' is more appropriate to these activities. Further my interpretation makes no distinction or stipulation as to the level of expertise of the intitiator. As examples I offer The use of empty oils drums by the financially constrained British to assess blast damage from nuclear tests. The creation of new oil replacement chemical technology by the Germans in WWII, and later the South Africans when under embargo; both were starved of oil. Columbus reaching America going west trying to reach China when the silk road was closed to him.
-

Cardinality of the set of binary-expressed real numbers
studiot replied to pengkuan's topic in Mathematics
As I understand the reasoning Every decimal number of length (after the point) n can be expressed as a fraction by adding n zeros to 1 on the bottom. In other words the cardinality of the decimals is the same as that of the rationals. But there are real numbers which are irrational. That is they cannot be expressed as a rational fraction. So there are additional real numbers that cannot be paired with a rational so there are more real numbers than rational numbers. So the cardinality of the reals is greater than that of the rationals. -

Cardinality of the set of binary-expressed real numbers
studiot replied to pengkuan's topic in Mathematics
Easy there. There are real numbers that cannot be expressed in decimal. There are different real numbers that cannot be expressed in binary. Decimal numbers are (i think) countable, but real numbers are not. https://en.wikipedia.org/wiki/Irrational_number You need the Schroeder Bernstein theorem to compare cardinality of these infinite sets. https://www.google.co.uk/search?q=schroeder+bernstein+theorem&hl=en-GB&biw=&bih=&gbv=2&oq=schroeder+ber&gs_l=heirloom-serp.1.0.0l4j0i22i30l6.2735.7485.0.9953.13.13.0.0.0.0.172.1735.0j13.13.0....0...1ac.1.34.heirloom-serp..0.13.1735.P-9FaKSEh3w -
Well I don't agree with this discussion about the box, or the sanction of DevilSolution for discussing it further, although it is off topic. +1 If folks really wnat to debate 'thinking ouside the box' then it should be in a separate thread. This one is about Newton and gravity. My answer is By the standards and knowledge of his day, Newton was not wrong. If we applied modern statistical techniques to the data known at the time of Newton's gravitational hypothesis it would support his hypothesis to a high degree of confidence. He was, however, troubled about the concept of 'action at a distance', but observed that his hypothesis fitted the known facts and could be extended to make predictions that were then verified. In my view, Newton was the greatest scientifc genius ever and his theory of gravity was ideally suited to the knowledge of mechanics available in his day.
-
Did you have a real question amongst all that rambling? Because if you did you hid it too well for me to find.
-
You haven't said whether this is in relation to school or college/university. There is a big difference. At school you have to (are supposed to) learn everything about all the subjects. Further the syllabuses are specified in great detail. You are not expected to know things they haven't told you, or work out for yourself the important key points. The key to school success is practice, practice, practice. But take heed of the words of others here about lengths of individual sessions and breaks. At uni you can't learn everything about a much more narrow subject. Not only do you specialise but each college includes or omits different material and their syllabuses are much briefer, more general and more loosely defined. Further they are expecting you to begin to think for yourself so everything is not spelled out in excruciating detail. So it is important to pay particular attention to the material presented and extract the key points. You study should include some fill-in and extension or reading round the subject. Discussion with your peers is always good. Unless you have started taking kryptonite pills you should still take heed of the words of others here about lengths of individual sessions and breaks. Go well in your studies.