-
Posts
18423 -
Joined
-
Last visited
-
Days Won
107
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
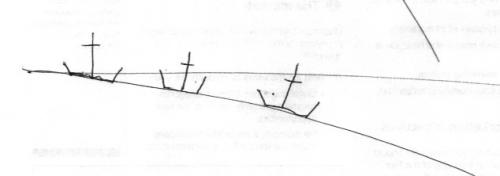
Having cleared the calculation issue let us move on to your next misconception about horizon views. I repeatedly asked what was seen from the dockside as a ship sailed away. There was a very good resason for this, as my rather scruffy sketch demonstrates. As the ship sails away the lower part disappears first, so in my sketch you can see first (closeup) the whole vessel dwon to the waterline. But as it moves off you get to the point where only the scuppers and above are visible. Next the lower mast disappears. Finally the cross tree, followed by the upper mast. You do not see this effect unless the object is moving away from you (This is one case where relative motion is asymmetric) So you would not see it from your canoe. Nor would you see it with two railway lines at the same level. Of course what you can see also gets smaller due to perspective as the object gets further away, but the point is not its size but its profile.
-
Everyone is stationary relative to themselves or in their own frame. It is possible for two 'someones' to be in the same frame, for example a railway train standing at a station and the track & station are in the same frame. In order to observe someone moving the observer has to be in a different frame. So the observer on the parked in his car by the station paltform sees himself stationary and the train moving (when it moves off) But also an observer who sees both someones moving is in yet another frame. So the observer standing on the station platform sees both the moving train and the car when it moves as moving. By the way did you revisit this thread of yours lately? http://www.scienceforums.net/topic/92850-accuracy-of-a-statement/
-
Xerxes. Consider post#16 quoted Yes a tensor conforms to the vector axioms for vectors. It is also true that group elements may themselves be operations.
-
Oh, what a minefield. Generalisation v restriction is where I think so many discussions go astray. If we start with sets we have operations from one set to another - morphisms. These can be very general and apply to sets of non mathematical interest so we restrict the sets under discussion to certain types of set. Groups. These are sets of elements of mathematical interest which have one defined operation between them. This operation is often called multiplication, but as we shall see this can lead to substantial confusion so I will call this the group star operation. For this star operation group axioms guarantee that 1) For any two elements a , b the star operation will produce a*b = c 2) There is an element e such that a*e = e*a = a for every element in the group. 3) There is another element in the group a such that aa-1 = e for each element in the group. [aside] Note there is no guarantee that a*b = b*a. This possibilty is the underlying pure mathematical reason for the Heisenberg Uncertainty Principle, from which it can be derived. [/aside] Now for the tricky bit. We are discussing numbers. So we restrict our set further to fit with numbers and their properties. For the real numbers the above axioms Are satisfied by the arithmetic operation of addition Are not satisfied by the arithmetic operation of multiplication (no inverse for the zero element) But we add the property that a*b = b*a, making the group abelian. So the group star operation is addition though some call it multiplication Let us move on and restrict still further, adding a second operation and forming the group into a ring. We already have arithmetical addition so we add arithmetical multiplication. So this ring has an (arithmetical) additive inverse but no (arithmetical) inverse as I said. Now please let us stop squabbling and move on.
-

What is the minimum number of properties posessed by members of a set?
studiot replied to studiot's topic in Mathematics
OMG What a prime slip up. My brain was clearly short of food. -
Perhaps you can point me at your reply to my post#35? The calculation is one of the most common in civil engineering surveying since it involves the deviation of a circular curve from a straight line tangent. The formula in question is not a linear proportion as you suggest but is [math]Offset = \frac{{{{\left( {Dis\tan ce} \right)}^2}}}{{2*Radius}}[/math] If we put in one mile (working in feet) then [math]Dip = \frac{{1*1*5280*5280}}{{2*20,900,000}} = 0.7'or8inches[/math] Which is the 8" figure you have found But look what happens, because the formula is not proportional, when we put in 32 miles (in feet). [math]Dip = \frac{{32*32*5280*5280}}{{2*20,900,000}} = 683'[/math] Yes six hundred and eight three feet.
-
One counterexample is enough to disprove any assertion. All that was required was to improve the wording. Both rings and fields have two binary operations defined. There are rings that have no zero element, but as far as I know, there are no fields that possess this characteristic.
-
Exactly. Thank you for demonstrating my point to Xerxes. Yes, but conway is currently suspended and cannot answer for himself, particularly in the now closed thread where his interpretation of the nature of a set was superior to that of Sato (and actually confirmed in the link that Sato provided) It is regretable that acrimony creeps into discussion with conway, all too readily, but he is not always wrong. I am hoping to avoid such in the discussion with Xerxes in this thread as I only posted in the hope of a gentle nudge to tighten up his wording to exclude countercases, once conway had weighed into the discussion. I had previously intended to do this by PM.
-
The problem is this is a false figure. Rather than cat calling, I have several times offered to explore your misconception about this with you to help you find out the truth. Each time the silence from your side of the border has been deafening.
-
There is no call to be rude about it. Just tell me what the multiplicative inverse of the zero element is in the field of real numbers please. That is what is 1/0 ?
-
I think you might like to check your mathematics dictionary as I would say you have the underlined almost the other way round. However I agree that the topic is hugely enormous and very confusingly full of special terminology. For this reason I offered (and unfortunately was rejected) my rough guide to sets in pengkuan's recent two threads. In fact there are several recent threads going about this very subject and its terminology by different authors so I was going to point this out in conway's last thread, untill it was closed a second time, though I do not know why.
-
Each time I have posted in this thread I have offered a polite and friendly scientific answer to one or more of your questions. I have also attempted to make the subject more interesting by additional comments that I think might be interesting and enhance the discussion. Each time you have avoided responding until pushed. In particular in my post #16, I offered the point that evidence is provided by ships disappering over the horizon. Ophiolite repeated this point in 2(a), post#26. In your response in post #33 it is clear you do not understand the significance of this point. It is an important point since it was Man's first recorded inkling that the Earth might be curved in some way, not flat. The ancient greek philosophers who noted it had a good understanding of perspective to realise that another effect that could not be explained by perspective was occurring. They also realised why this discovery was peculaiar to the marine environment and dould not reliably be applied on land. So, when offered detail from folks who are well qualified and experienced you can either rush in where angels fear to tread or ask for clarification if you find that detail not sufficient.
-
The number of bits of information a system can hold is the number of different states it can exist in. So a system that can be liquid or gas can store two bits of information, one for liquid and one for gas. The definition of states can be very wide indeed In statistical mechanics it is the number of energy states. In electronics it can be the positions of a switch. In some circumstances the variable used to define state can vary continuously and the number of states is then infinite. Velocity would be an example. Iin some circumstances it can only vary in steps, eg the charge on a capacitor, which can only vary in steps of one electron charge.Here there are very many, but not infinite, states available between minimum and maximum charge.
-

What is the minimum number of properties posessed by members of a set?
studiot replied to studiot's topic in Mathematics
Good morning wtf, I did not use (or intend to use) ‘accuse’ in a defamatory way or feel insulted by you suggesting I might be confusing the properties assigned to sets and those assigned to elements of sets. Nor do I wish it to detract from an excellent discussion. Indeed had I mixed them up you would be well justified in ‘accusing’ me of doing so, but I don’t think I did. In my mind this thread probes some of the dark corners of Mathematics, so it is not surprising that some spiders crawl out. J The introduction of KFC or its variants limits the scope of the discussion since KFC does not apply to all sets or even all mathematical sets. The foundation axiom limits KFC sets to those for which an epsilon minimum can be defined. The set of symmetries of a regular hexagon, for instance, has no minimum, though it obeys many of the other axioms. I am sorry I originally misinterpreted your post 24 to mean that your set V comprised the set of rationals. I see now you were meaning a proper partition into equivalence classes. (More on this and my hexagon later) I am not aware of any KFC axiom that requires all sets to be partitionable. How do you partition the zero set without invoking a circular argument? If, however you start with a set such as the reals and divide it to obtain a counterexample set then surely you must start with an isolated element and show first that it is a real, before you can allocate it to your set V or the set W of the remaining reals not in V. In my example I did not start with a set and cut it down I obtained elements and assigned them to my set that I was constructing. So the elements of my example set entered the set without carrying any preassigned properties with them. The requirement that an element of a set be ‘distinct’ does not mean that we should be able to identify it ‘in the wild’. In fact it does not even apply to a single isolated element, but to (at least) two elements so that they may be compared and distinguished as the same or different. Nor is our ability to identify an element a bar. Many differential equations are known to have solutions, even though we cannot solve them. So we know there exists a set of solutions, even though we do not know a single one. Bringing in a second element brings me back to my hexagon symmetries. These are often stated as forming an equivalence class. This is true so long as we are only considering an isolated symmetry. But bring in a second symmetry and things change. It makes no difference which vertex of a benzene ring you attach the first functional group to. But any chemist will tell you about the difference between the ortho, meta and para positions for introducing a second group. Chirality has raised her head. And yet again this issue does not arise with the set of symmetries of an equilateral triangle. So thank you again for thought provoking probing of my discussion. As the old scribe said, I look forward to your reply. -

Explaining The Corrosion Of Iron In NaOH With Equilibrium
studiot replied to LoganJohnston's topic in Homework Help
Iron stops rusting at high enough pH, which is why reinforcing bars don't rust in concrete. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=ph+to+stop+iron+rusting&gbv=2&oq=ph+to+stop+iron+rusting&gs_l=heirloom-hp.3...1953.9172.0.9984.23.2.0.21.21.0.141.282.0j2.2.0....0...1ac.1.34.heirloom-hp..21.2.282.cfqLBSQ60cA -
I think it's a little different than that.
-

What is the minimum number of properties posessed by members of a set?
studiot replied to studiot's topic in Mathematics
Firstly elements may have other properties than they possess as elements of a particular set. Such properties are irrelevent to their member ship of any particular set. I can't understand how you can accuse me of confusing the properties of elements with the properties of sets, considering the title of this thread. Unfortunately your counterexample is not such. You start with the set of real numbers. So every member of the set has the property of being a real number. property number 1 You then select some memebers that have the property of being rational property number 2 I make that two properties. So the set of rationals inherits the property of also being real. I thought I gave an example of a set where the only common property of the elements was being on the membership list, but that does not prevent them having other irrelevent properties. -
I hope so too. If I didn't think conway had started sprinkling the red dust around, undoing my encouragement for Sato, I would point out to him that case (3) is probably the zero he is looking for.
-
Hello Strange, I think you have to be careful here as the terminology is confusing. Is the introduction of set theory appropriate because zero is an element of some sets, as well as a set in its own right in some circumstances. It is very easy to become confused between sets, elements, the relationships between sets and the relationships within sets (i.e. between elements) and properties of sets and properties of elements. This is particularly so when the elements themselves are sets in their own right. Here the terminology is not universal. I like Simmons' approach to call sets of sets 'classes' when there is any doubt. Anyway you are not strictly correct to say that zero 'is' a set. Consider the following. Let there be a set of elements. S, denoted {a, b, c , d} etc, equipped with a relation between elements, called multiplication, that produces a member of the set. a * b = a member of the set [math]If\;(a,b) \in S\quad then\quad (a*b) \in S[/math] Three possibilities arise 1) a * b = c where c is different from a or b 2) a * b = a for every a in the set 3) a * b = b for every a in the set Result (2) makes the value of b one: 'b' is then known as the identity element Result (3) makes the value of b zero: 'b' is then known as the zero element But not all sets have an identity element or a zero element or both.
-
Firstly a small correction The word is spelled pendulum Yes you are right the period of the pendulum is equal to 2pi root (l/g). Note the brackets I have added to make the formula clear and correct. However the acceleration term is not g when there are additional forces involved. Remember acceleration = net force / mass The mass has not changed but the net force has changed due to the additional bouyancy force which acts to reduce the gravitational force (weight) and therefore the acceleration. So the pendulum swings mores slowly under water. Here is a record of a practical experiment and explanation. http://www.millersville.edu/physics/experiments/038/index.php
-
I was congratulating Sato on his distinction between a set and a space. A set is the more general object. Here is Simmons' version of the statement You should be aware that the words 'set', 'space' and 'relation' have special meaning in Mathematics.
-
+1 Which affects what parameter in the formula for the period of a pendulum?
-
First time I've seen that fundamental definition of sets and spaces distinguishing the two, pointed out here at SF. There are some others who could also benefit from noting this. +1
-

What is the minimum number of properties posessed by members of a set?
studiot replied to studiot's topic in Mathematics
Good morning wtf, and thank you for your contribution. The question in this thread is about the minimum number of properties possessed by an element, not the set properties. In the case of your examples each element has multiple properties. So I am interested in sets where the elements have only one property; I have displayed such a set. Since such a set can be displayed, there cannot be an equivalence relation on this particular set. As regards to your constructed partition of the reals, As I understand it, you have partitioned the reals into two sets: the rationals (you have called set V) and the rest (I am calling W) Consider any [math]a,b \in V[/math] Then [math]\left( {a + b} \right) \in V[/math] Thus a and b have at least two properties. -
Those who made too much of units had a point, but went too far IMHO. If your numbers had worked out, your statement could have been made too work with suitable adjustments, Instead of attacking the whole idea. Consider the following (correct) statement. There is always one more post than panel in a fence with no gaps or loose ends. Two different units, but it is possible to compare the numbers.