studiot

So far as I can make out your list of unsupported claims is totally disconnected from the examples in my post you quoted in its entirety. So do you pay any attention to what others write or was quoting my post just a slip o' the mouse?

Very clear statement , andrew. +1. turpint, This was the great breakthrough by Newton when they realised that bodies will continue indefinitely in their state of motion if you leave them alone. It is common for beginners to think otherwise and it was believed for centuries before Newton. One spin off from that. It takes no energy for the body to keep on in its state of motion (or rest). The body has energy by virtue of its motion, but it doesn't loose any, just because it is moving. If it does loose energy and slow down this means that a force must be acting on it (eg friction, air resistance etc)

It might do. If you have more unknowns than equations, differentiation/integration is one way to get more equations. This occurs in structural engineering where you know the slope is zero so you can differentiate and set to zero. But you should not say nonlinear sets of equations. It is not the set which is linear or nonlinear. That is meaningless. It is the equations in the set or at least one of them which is/are non linear.

So how did your query arise? You need to put more in here to get more out.

So he was not completely 100% correct has anyone ever been in history? And are you trying to discredit an entire list by gnawing at the edges of one entry?

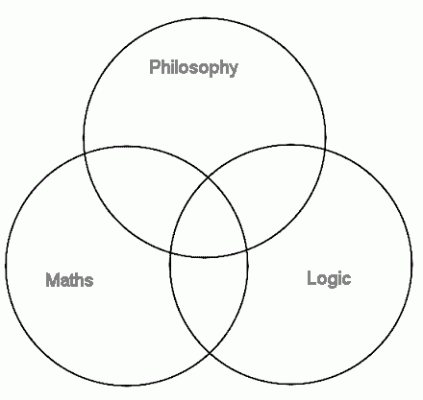
It is a logical fallacy to lump all posters together like this and then say Particularly as you are articulating what I said in my Venn diagram and extracts from the OED.

Much research is kept secret for commercial (as with Tesla) or state security reasons (as with Turing). The original post referred to discoveries that were public but opposed by powerful figures at the time and were later shown to be correct. If they were not later shown to be correct we could not know them as failures of the scientific system of the time. Just because it was kept secret does not mean it was opposed, discarded or ridiculed. So Tesla is not a good example. However I agree with the basic premise that there have been too many instances of opposition to genuine innovation. Whilst it is easy to point to instances back a few hundred years into history, twentieth century examples might werll include De Haviland Whittle Barnes Wallis The inventor of the bazooka, whose name escapes me but was not as Wikipedia describes. Wegener Bayes (I include him here because the bayesian war was particularly intense in the twencen) Porsche Late Nineteenth century pioneers Parsons However I'm sorry I don't see that anonymity would lead to an improvement. Anonymity has its place in for instance blind and double blind testing, the conduct of proper examinations and so forth.

I strongly endorse that view. Or to put it another way. Not all thinking involves words. Not only is there a vast body of evidence to support this, it is commonplace experience by most (I hesisitate to say all) humans. Acting in three dimensions involves processing sensory input information and direction future action accordingly (thinking). This skill is used in pickup up a pint of beer, driving a car or an aircraft, the list goes on and an. Many people report that they think in pictures, not words. Some think in musical sequences. and so on and so on.

A weir controls the flow and flow regimes of the water particularly when the flow is low. As water and flow levels rise, it has a decreasing effect on the water. The hydraulic characteristics of the weir in relation to the flow, depend, amongst other things, upon its length (e width across the river). The 'fingering' pattern of the layout increases this length considerably. Your pictured weir is the subject of current improvement and naturalisation plans. and http://thamesriverstrust.org.uk/projects/river-brent-eel-pass-projects/river-brent-eel-pass-inception-report/ http://www.thames21.org.uk/wp-content/uploads/2014/05/brent_river_corridor_improvement_plan_final_2014.pdf

Perhaps I should have given the full reference G H Hardy A Course in Pure Mathematics (10 Ed 1952) Cambridge. I do not have his series book. However the following extract from Fort 1930 Infinite Series Oxford proves $\sum\limits_0^\infty {{a_a}}$ the infinite sum tends to infinite (Theorem 32) and the finite sum converges (Theorem 33) Ferrar A textbook of Convergence Oxford 1959 Has a similar discussion to my Hardy above.

Yikes

Unfortunately p333 of my 10th edition Hardy contains miscellaneous examples on chapter VII (additional theorems in the calculus), not your referenced comment. Secondly I can't trace your other references of the form 13.17 and 13.10.11. However in Chapter 1V (Limits of functions of a positive integer variable) where he proves the theorems I referred to he discusses the use of sums and products of infinite series and shows that the conditions of allowability of manipulation by mathematic is that the series is convergent. But (my comments now) the theorems above show that the series is not convergent so those manipulations are disallowed.

So there is considerable overlap.

+1 I like it. and you can spend the saved money on good single malt.

I hope that was a joke, but I will explain if you require.

Hardy p342 Theorems on series. 1) A series of all positive terms must be convergent or diverge to infinity 2) A necessary and sufficient condition that Sn is convergent is that there exists a number K such that u0+u1+u2+u3+.............un < K for all values of n For any K, Let un = K Then Sn > K Hence by 2 the original series is not convergent Hence by 1 it is divergent to infinity.

This question lends itself to a Venn diagram for discussion. But only so long as we can agree boundaries and there is only one ring for each of the three words.

I though I gave the reference clue to look up. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=quadrivium&gbv=2&oq=quadrivium&gs_l=heirloom-hp.3..0l10.1906.4813.0.5156.10.9.0.1.1.0.187.1219.0j9.9.0....0...1ac.1.34.heirloom-hp..0.10.1250.gTxBIo5Xegg The four disciplines of the quadrivium is the origin of the plural in the word 'mathematics', although today we use it as if it were a singular noun.

I don't know if this is the correct place to put this but there is a new art exhibition (by a scottish lady sculptor) opened in London. This is called anthropocene, after the latest geological age to be identified and provides a 'spine' of linked scultpures linking the geology of the British Isles over geological timescales. http://www.angelaspalmer.com/ I apologise if this is considered advertising, but is it also of scientifc merit.

You all seem to be missing the point. The boundaries of all three words, maths (with whatever spelling), logic and philosophy are not clear or rigid, neither is what is included or excluded. It is not even clear if for each one there is one system more than one system. So the original question, as posed, is too vague to be meaningful or properly answerable.

With the greatest respect, have you read the OED lately? To quote the philosopher R G Collingwood

You have mathematics (maths) in the plural so the first need to to clarify Which Mathematics? (I refer to the quadrivium) The second clarification needed is to ask do you regard philosophy as singular and in that case what is included?

I don't see that the centroid (or centre of gravity) is purely mathematical, simple versions were included in my O level Physics, not in my O level Mathematics. It was in both A level (applied) Maths and Physics. It did not appear in maths degree, I do not have a physics one to compare, but it was heavily used in my engineering degree, where it was assumed to be known about. $\bar x = \frac{{\smallint \smallint \smallint \rho xdxdydz}}{{\smallint \smallint \smallint \rho dxdydz}}$ But yes the centroid is a property of an object, but not a material property. And it is time independent. Density is a material property.And it is time independent. $\rho = \frac{m}{V}$ Another object property is the metaheight used in floating bodies such as ships and icebergs. $h = \frac{m}{M}d\cot (\theta )$ I know I said the focal length of a lens but I was really referring to the lens equation, which is time independent. This is more than just a property, is is a relationship between three physical quantites. $\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ Charle's law is time independent, and enjoys the status of a Law of Thermodynamics in Physics. $\frac{{{V_1}}}{{{V_2}}} = \frac{{{T_1}}}{{{T_2}}}$ I don't know if you would include balanced (stoichiometric) chemical reaction equations but they are time independent but refer to change. $C + {O_2} \to C{O_2}$ So I think the examples are there if you care to look.

What is this in relation to? Are you asking about conservative and non conservative fields or forces? Gravity is conservative, friction is non conservative. Or are you asking about zero v nonzero curl?

Steel dust? Are you trying to clean up the result of grinding? The resulting powder will be mostly carborundum or similar. More information please.