studiot

Perhaps you would like to rephrase this?

Would you like to explain this. It makes no sense to me. Nor does showing pictorial sequences of allegedly convergent or divergent boundaries all the same distance apart. I would suggest you need to conduct some old fashioned geological investigation before offering some of the above statements of geological history. You should check that the actual rocks found in the field conform to your theory. Are they of the correct Age? Are they of the correct type - sedimentary or igneous? What is the orientation of their bedding? Are they the right way up or is there an inversion unconformity? For instance a recent poster failed to do this with another theory of the Himalaya http://www.scienceforums.net/topic/91603-evolution-of-himalayas-and-tibet-and-the-great-volcano/ And failed to realise that the region comprises two distinct blocks one sedimentary and one igneous. Please make sure you do not fall into the same trap. Incidentally no one here is trying to cleverly trap you. But we will rigorously test your statements for logical consistency, both with known observed facts like the known geological maps and sections and other measurements, and internally with themselves. Nice to see you back.

Brett, please note that Strange offered you a formula involving delta t or time differences. Your formula involves t or time alone. That implies some sort of absolute time or time synchronisation between two reference frames, which you cannot have.

Yes, Mr Zeeman induces them.

Sounds good, but In even modest sized outfits the telephone and broadband is no longer powered by the telco line, it is powered from the same mains as the server. So unless you also have a UPS on you telecoms equipment your server will be unable to send an Email.

It is a question of patiently putting in the correct masses and friction coefficients at the appropriate points. I don't get exactly the same results, but it would depend upon the value adopted for g. Here are my calculations 1) [math]acceleration = \frac{{Tension}}{{totalmass}} = \frac{{248}}{{92 + 17}} = 2.275m/{s^2}[/math] 2) [math]Force = mass*acceleration = 17x2.275N[/math] 3) [math]Max{F_{top}} = mass*\max acceleration[/math] [math]0.8*17*g = 17*{a_{\max }}[/math] [math]{a_{\max }} = 0.8g = 0.8*9.81 = 7.848m/{s^2}[/math] [math]Max{F_{total}} = Mas{s_{total}}*{a_{\max }} = 109 *7.848 = 855.432N[/math] 4) [math]{F_{topsliding}} = Mas{s_{top}}*acceleratio{n_{top}}[/math] [math]0.62*17*g = 17*{a_{topsliding}}[/math] [math]{a_{topsliding}} = 0.62g = 0.62*9.81 = 6.0822[/math] 5) [math]acceleration = \frac{{netforce}}{{mas{s_{botom}}}} = \frac{{Tensionpull - frictionfromtop}}{{92}} = \frac{{1223 - 0.62*17*9.81}}{{92}}12.17m/{s^2}[/math]

As regards the decay, the is a difference between the rate of decay and the decay itself. The rate of decay tends towards the exponential curve as the number of trials tends to infinity. The decay itself is random. This mean that if you lined up 1,000,000 U238 atoms and i pointed to number 1093738 in the row it's decay or not would occur in a totally random fashion. That particular atom could be stable for longer than the age of the universe or it could decay in the next second, and you have no way of predetermining which will occur. That is also why we can construct a clock from radioactive decay, as I said earlier and why this process can also be used to show the need for a time coordinate as well as measure it. Length is not involved, only number.

Fully random? Does your claim have a meaning other than being just plain wrong.

No it is a much much much wider subject than that. Most mathematics is linear, and the first approach to any non linear maths is to try to linearise it (=find a linear approximation). You really need to find out and understand what linear maths is. I do not mean study all its ins and outs, that would take years, just find out enough to recognise what is linear and what is not and to appreciate the principle consequences of that distinction. The following polynomical falls into the ambit of linear maths y = ax6 + bx5 + cx4 + dx3 + ex2 + fx because it is a linear combination of basis polynomials x6, x5, x4, x3, x2 x. this polynomial does not (is non linear) y = x + xy Note the word is basis not base. Detail is important in mathematics.

'close to' is introducing the mathematica (topological)l concepts of connectedness, neighbourhoods, compact sets, all of which I think are violated by the big bang itself.

A graduate introduction..... ???? Have you studied linear algebra and in particular do you know what a basis is ?

1) Exactly why I think this subject needs a good airing, rather than attracting ridicule. 2) So perhaps you would be kind enough to suggest a better or improved one.

I am not a cosmologist, and have little interest in it. The introduction Minkowski spacetime as a theory predates the big bang as a theory by several decades and I think that the introductuion of the big bang requires severe modification to MST if not something else entirely. There is an interesting mathematical point to be made here. Much of mathematics is based on collecting together into sets objects, points, 'events' or whatever that have common properties. That is what a manifold is. A set or collection of points with a specific list of (mathematical) properties. Two properties are desirable for such sets because then we can do extensive mathematics on them 1) The set contains all points with the particular property list. 2) The mathematical processes we employ (functions, transformations operations whatever) connect one member of the set to another member of the set. They do not take us outside the set. So adding 3 to 4 produces 7, another number in the set. It does not produce a triangle Processes which lead to a result that is not a point in the set are called singularities (amongst other things). Processess which involve the conjunction of an infinite number of points sometimes lead to a result that is not a member of the set. For instance Fourier analysis applies to continuous functions in linear analysis, and a fintite combination will always produce another continuous function. But it is possible to construct discontinuous functions with an infinite number of points. So perhaps the big bang is not a valid member (point) of Minkowski spacetime.

Sorry, John, I thought that this was all part of my answer that I am not designing any sort of controller so don't need to consider alternatives. That does not mean others are not designing such a system (it is after all the logical next step from datalogging and parameter setting) and my query wonders how folks would react if they met one in a bar.

You can declare any point in the manifold 'zero', but it is arbitrary, just as declaring 0o longitude to pass through London is arbitrary and Hawaii would have done. This brings up another important point. About the word curvature. Using the 3D formula I quoted above, all the distance lines between any two points A and B remain in the manifold. That is they do not pass through points not in the manifold on their 'way' from A to B. If we consider our manifold to be the 2D (surface of the ) sphere with coordinate lines of latitude and longitude then lines, generated by the 3D formula, between points A and B on this surface pass through points not in the 2D manifold. For this to happen we say that the 2D manifold is curved in 3D space and embedded in it. The alternative is to use more complicated spherical trigonometry (or worse) formulae which keep all lines within the manifold. This is the reason why we need more complicated formulae when we want to discuss the physics of the 4D manifold - we do not want the embedding in a yet higher dimension.

Thank you all, lots of thoughts and meat for discussion. My answers to the specific questions, sorry if I've missed one, please point it out. No I am not designing a Windows or any other gas boiler controller. The only experience I have is a Windows operated data logger for a large commercial office. This has no controlling functions for the boiler, but can set or change parameters in the boiler's hardware contoller. The last non functioning ATMs I saw were outside the Cydesdale Bank in Dundee, earlier this year. But I agree they are generally pretty reliable. Studio T does, however maintain embedded Windows POS (point of sale) units in some large commercial operations. These are substantially more reliable than the 'secure' Windows networks in those same organisations. (Windows server domains and pro workstations). They are not as reliable as ATM units though, producing system errors that require rebooting to clear.

All of these questions can be answered by understanding what is meant by the '4D distance' Unlike 3D distance the 4D distance has components that add to it and components that subtract from it. In 3D the distance (also called the metric) is given by (d2 - d1)2 = (x 2- x1)2 + (y2-y1)2 + (z2- z1)2 The things to notice here are that because they are all squares they are all positive and that all the components are added together. So any component value at all will contibute to increasing the distance. In the 4D spactime manifold this is not the case. The distance, now denoted by s, is given by (s2 - s1)2 = (x 2- x1)2 + (y2-y1)2 + (z2- z1)2 - c2(t2- t1)2 There is now a term that can subtract from the overal value of distance so a large contribution from the additive components can be offset by a large contribution from the subtractive one and vice versa. Note that this is the standard metric for this work in special relativity, but there are other more complicated ones available that are used in general relativity.

So my Windows just bluescreened again. What would have happened if it was supposed to be controlling the safety interlocks on the boiler?

The title says it all. Let the discussion commence.

I'm glad you found this helpful. It seems to be the season for starting numerical methods courses. See here for information about some of the other numerical topics you listed. http://mathhelpforum.com/higher-math/252777-approximation-function-vs-interpolation-function.html and here http://mymathforum.com/math/252860-square-root.html The point about the spreadsheet is that it provides a quick and easy way to play with formulae. Another (teaching) webiste for this is https://www.geogebra.org/ This allows graphics, formulae and spreadsheets very simply and is open source which means it is freeware. I cannot tell you everything in one single post but I do ask a few questions designed to lead to the next one so please answer them if you can. Your example can demonstrate considerably more about the important points in numerical methods, if you wish to continue. The standard quadratic equation formula (which we are not supposed to be discussing here) works perfectly well for complex solutions. It's just that the solutions are well, complex numbers.

First, and I cannot stress the importance of this enough. You have exact solutions in this case. Numerical methods are all about the real world. In the real world your equation is likely to be presented something like 1.0057X2 - 11.993725689X - 28.000000007 = 0 and you are not sure about the last few digits of any of the coefficients. This is where you will use numerical methods to get not an exact answer but an answer that is good enough. Back to the example, please note that this forum allows the use of superscript and subscript (you will find them on the second row of the toolbar) to better present mathematics. Your equation is 1X2 - 12X- 28 = 0 rearrange 12X = X2 -28 X = (X2 -28) / 12 Now look back at the formula I presented in post 2 We have a formula for X, but it is in terms of X. If we take a 'guess' for X and insert it into this formula we can calculate another value of X. If we take this new value of X and insert it into the formula we can calculate yet another value for X and so on. The hope is that each 'iteration' (=approximation) will get better than the last and the calculations will converge on the correct answer. That is why this is called the recursiv.e or iterative method. I have shown the results of doing this in the spreadsheet. Have you any experience with spreadsheets?

I am guessing you have just started a course in numerical methods and have found it all very different from anything you have seen before? You are right to try to find examples where you can compare results with what you can find by other methods. Other methods usually mean what are known as closed form solution that you can extract a formula which will give you the 'absolutely' correct answer. But even then working this out may take more effort than finding the answer by a numerical proceedure.Y You have provided an example, how about we work through my solution, picking out the essential points of numerical methods, as I suggested above?H Have you found the two solutions to your quadratic by formula?

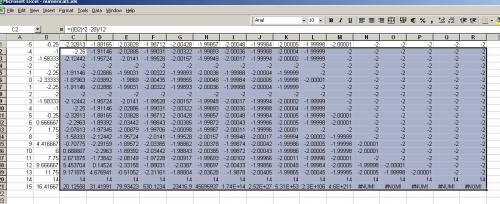
I don't know what you don't understand about numerical methods, you will need to explain further. Which methods? Here is a spreadsheet showing the effect of a recursive numerical method using the formula [math]{X_{n + 1}} = \frac{1}{{12}}\left( {X_n^2 - 28} \right)[/math] seeding the Xn from -5 to +15. As can be seen this rapidly converges on the -2 solution, but not on the +14 one.

The solution of the Schrodinger equation applied to a periodic structure such as a semiconductor lattice leads to a complicated trigonometric equation which has real solutions that work in transistors and imaginary solutions that have no physical impact. For example the simplest approach is the Kronig-Penny model. https://www.google.co.uk/search?hl=en-GB&source=hp&biw=&bih=&q=kronig+penney+model+band+structure&gbv=2&oq=Kronig+Penn&gs_l=heirloom-hp.1.2.0l10.1859.5031.0.6922.11.8.0.3.3.0.281.1515.2-7.7.0....0...1ac.1.34.heirloom-hp..1.10.1640.q8b6bmRKGAY You are probably aware of the technique in elementary physics of 'equating real and imaginary parts and discarding the imaginary results'. There is a particularly clear working of this in Prof Atkins' book, Molecular Quantum Mechanics, p269ff.

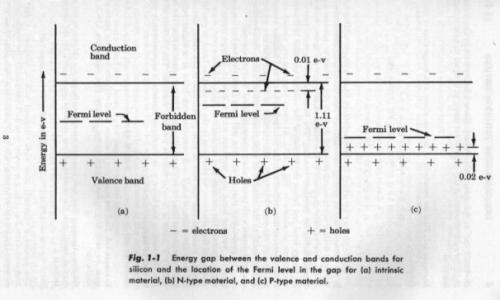
Silicon is a semiconductor and a solid in normal circumstances so passing electric current through it by applying a voltage will not result in ionisation. Edit Actually, to be fair, it is a somewhat disingenuous average to use 0.6 volts as the bandgap (= the forbidden zone) for pure silicon is 1.1 volts. But silicon is usually doped. In the solid state silicon is covalently bonded giant molecule, also called metallic bonding. It does not ionise with the passage of electricity, it merely heats up, through ohmic heating, and eventually melts to liquid silicon comprising covalent molecules or individual silicon atoms, both of which are neutral. Solid state physics and chemistry is fascinating, but you are opening a big subject and adding phase diagrams makes things even bigger. Do you want to proceed?