studiot

Here are a few short thoughts, as it's getting late here. Taught yourself linear algebra. That's something to be proud of and the subject is the basis for many (if not most) of useful mathematics. Tensors take you back into the theoretical arena and a really a part of linear mathematics anyway. Interpolation is definitely in the applied mathematics camp, sub category numerical methods. Note I said numerical methods. There is a much more theoretical subject of numerical analysis. No there is not one (or even a few) grand methods, there are many approaches. We can continue to talk about them if you like, this is a very pleasant thread, much better than those where there is constant arguing for the sake of it. But remember my views are skewed towards the applied side and I make no apology for this. I would say that you would be better advised to look at Hamilton - Lagrange methods and what is called "The Calculus of Variations", rather than pursue tensor methods very deeply. The purpose of the calculus of variations is to determine the best curve through data points according to some pre established criterion. Finite element analysis is when you draw up a (multidimensional) grid or mesh and fit it to whatever you are analysing. You must have seen this in the movies or adverts where a computer 'scans' the hero or a car or something. My avatar picture is a finete element mesh overlaid on a human face. Again we can talk about all this and I will also explain the finite difference table further.

There is not a human that has never mis-spoke. So surely in a Science forum we should not spend lots of time and effort on rehashing who said what? But rather discuss the best available knowledge of the theory.

You need to be very clear what is meant by both equilibrium and state. There are two (thermodynamic) drivers for the future direction of a system's state. Minimum Energy Maximum Entropy These two may be aligned or they may be opposed and the resulting state is then a balance between these two.

I think that there are more provisos needed to make this entirely true. Do you know and real isolated systems and would this apply to an infinite isolated system?

I am very flattered to think that the whole of my rushed explanation was crystal clear since you haven't asked any technical questions, but I'm sure it could be improved. So don't hesitate to ask about what was said. It would be useful at this point to ask what your level of mathematical/technical background is. The second quote sounds like you have seen the finite element grids used in modern analysis of just about everything. Do you know in principle what a diffeential equation is? I am not asking if you know lots of solutions, just if you have the general idea. Then I can give a better answer to the first quote above.

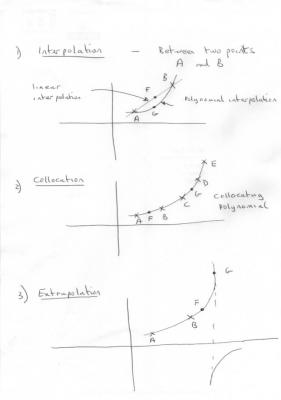
Here is the STRRGI (Studio T Rapid Rough Guide to Interpolation and other itches) Let us say we have a number of data points and wish model this by a curve of known algebraic form, so that we can use the curve to find data at points we do not have the true (or measured) value for. With reference to the figures, I have used large crosses to denote the known data points where it is assumes the values are exact and labelled these points A, B, C, D and E. Points where e want to estimate the value the data would take at these points are labelled F and G in all cases. First comes interpolation. Inter is Latin for between and interpolation is used to estimate the data value between two points. Obviously many different curves can be employed, but we want one that is ‘well behaved’. That is it does not go off to infinity between A and B or execute wiggles etc but in some way moves smoothly and continuously from A to B. I have shown a straight line and a polynomial (probably a quadratic) that have this property. Point F is located on the straight line and Point G on the quadratic, but both have the same x coordinate. So you can see that we already have two different possible estimates for the data value at this x. But we may have a set or table of data values that show a curve, not a straight line. If we model with a polynomial, the curve that passes through (has the same values as the data at ) A, B,C, D and E is called the collocating polynomial. It is said to collocate (be the same as or fit exactly) the data at these points. If we can generate such a polynomial we can have good confidence that points F and G on the curve will be pretty good estimates of the data at their locations. Lastly we come to extrapolation. Extra is Latin for outside and this is where we extend the supposed line beyond the interval bracketed by A and B. In the diagram F is close to B and we can reasonably hope that the estimate that F represents is a good match to the actual data. The further we go the more dicy this assumption becomes. It is a bit like leverage. The longer the lever greater the displacement. This is shown by Point G in the diagram. Point G also shows something else. Your constructed function (don’t worry about my contrived comment it only meant it was an exercise) was a tangent. The tangent goes of to + infinity and then returns from – infinity as shown. So if the data function really does this there is huge scope for error around this point. Now to change the subject entirely. Before the days of calculating machines, tables of mathematical functions were drawn up. Someone had to calculate all these values. How did they do this? You may well ask. Well not by exhaustive computations on series or whatever. That would have been horrific. The method used was the method developed by Newton and which he was playing about with when he developed the Calculus. It is called the method of finite differences, is was a way to obtain data values between entries in a table, from the existing assumed exact ones. The method can be used to obtain any desired level of accuracy if enough exact data points are available. That is the tables can be interpolated to any number of significant figures. Thus it is a method of interpolation and many observed empirical tables such as the international steam tables are still used in this way. Original sine, tangent and logarithmic tables were prepared in this way. As an introduction look at the final diagram which has 5 columns of figures. The first column is a list of the exact data, 1, 8, 27 etc The second column is the difference between successive real data entries so the first one is (8-1 = 7) The third column is the difference between these ‘differences’ So 19 – 7 = 12 The fourth column is the difference between these differences, which you will note are all the same The fifth column is again differences but they are all zero. All subsequent columns would also be zero. If you are observant you will note that the original data is cubic and the columns become constant on the fourth. This is no accident. A quadratic becomes constant on the third etc. So with enough data we can either use these values to reinstate a missing data point in the list, calculate the next one or insert a point partway between two existing ones. Because numerical data tables were once so important a huge body of theory has been developed about the best ways to do this.

I've had quite enough of comtemptuous comments thank you. They add nothing to a scientific discussion.

Yes I thought it seemed a bit contrived, but I did briefly wonder if there was any relation to the Langevin function.

You can solve for a, b and c because you have exactly the same number of unknowns as equations, so any solution (just have the same number does not guarantee solutions) is exact. If you have more equations than unknowns then, as always, you have redundant information. There are various methods of dealing with this, mostly statistical, which is what I expect you are thinking of. You can assume the form of the fitting equation and calculate a set of auxiliary equations minimising some functions of the deviations that yields a unique set of coefficients. the usual is to minimise the squares of the deviations producing what is known as 'least squares fitting'. We use the squares because they are all positive and thus we can minimise their absolute value. Other statistical methods are available if we want to weight the deviations to remove outliers etc. Another approach entirely may be more appropriate if we are concerned with the slope of the fitting equation at the end points because we can gain some extra equations by differentiating it and fitting the derived curve, at least at the ends. The most popular of this type is are called spline curves. This whole subject is huge. By the way, as a start do you know the difference between interpolation and extrapolation?

Can you offer the exact quote (from Einstein) that makes you think this?

You are not trying hard enough. [math]\tan \left\{ {{e^{a{x^2} + bx + c}}} \right\} = 0,\quad at\,x = 0[/math] [math]\tan \left\{ {{e^{ + c}}} \right\} = 0[/math] [math]\tan \left\{ {something} \right\} = 0,\quad something \ne 0[/math] [math]{e^{ + c}} = something[/math] Can you think of something, not equal to zero, that makes tan(something) zero? Hint tan is a periodic function.

You have three unknowns, a, b and c You can obtain three simultaneous equations linking them, by substituting the values for x and y at the known points. You then need to solve the three equations for the coefficients a, b and c. The first one should yield c directly, but think carefully about it, and note that angles will be measured in radians.

Hi Nick, I didn't see a definition of p from swansont - p is momentum. (Special) relativity is accessible to those in upper high school who have studied enough mechanics and calculus to know what momentum and a derivative is. Advanced mathematics is not necessary (Einstein was a physicist not a mathematician and argued as such). A good little book to understand the physics from is Relativity Physics by R E Turner It is one of the Routledge 'Student Physics' series for first and second year undergraduates. Yes indeed. A pedantic point perhaps but a true one nonetheless. In fact the c2 (L2 S-2) can be regarded as the necessary units of conversion between mass (M) and energy (M L2 S-2) You can use the fact that momentum = mass (M) times velocity (L2 S-2) to verify the dimensional correctness of swansont's equation above.

You stated This was a pretty insulting remark, again I have underlined the relevent part. To which I commented Now what part of this are you claiming is not true? Have you actually tried googling those questions? Or are you saying ajb is not offering facts? Since you were clearly intent on insulting everyone I left the thread for a while and then simply offered you something that might be useful in post#23. You have ignored this until now where your reaction is again dismissive, condescending, and insulting.

Is this how you regard those with an unimpeachable track record in their field? Or do you have such a low disregard for all your fellow men? Once again I have underlined the relevent part of the passage.

And the reference I gave you? Why are you still ignoring what is said to you?

Exactly how is this scurrilous accusation consistent with the following And why do you ignore the rules discussion and of this forum and consistently fail to even attempt an answer my question?

Which was why I posted a reading reference to some newly published stuff that actually gave consideration to your questions and acknowledged the known deficiencies in the General Theory of Relativity. But you ignored it

Only 2 pages?? huh!! I think I gave up after my posts 7 and 23.

Since you didn't bother to respond to my first reply, why should we bother to respond to any more of yours?

Whilst Joule performed many useful experiments that pushed forward the boundaries of science, he not produce the equation you mention. In fact no one person did it was a collaborative development during the 19th century, stating with Fourier in Mathematics. See the history of dimensional analysis here https://en.wikipedia.org/wiki/Dimensional_analysis

OK, so your stuff is too theoretical to get any large organisation behind you. Another route would be to publish as a conference paper. I assume you want to claim any discovery credit, which is why you are keeping discreet about the content. If you were to look around the conference circuit at a less prestigious one you might find that they would accept your paper for presentation at their conference, and once you have done that any credit that flows would be entirely yours. Attending such a conference would be cheaper than paying some publishing house. I cannot suggest any conferences as all my sources would be trade not academic / theoretical but maybe someone else here with better knowledge in that area will.

You say there is a new currently theoretical result available. Can this result be confirmed by any proposed experiment? If confirmed, would this result have any practical use? I ask this because there are scientific research companies you can team up with who would be happy to include you in any paper's list of authors if they thought there was a commercial interest. They might also help perform the experiment. I have done this in the past with a UMIST (University of Manchester Institute of Science and Technology) associated company.

Yes, as I understand it, icebergs are made of frozen drinkably fresh water. You can actually purify salt water by freezing. Care should be taken with the final sentence of swansont's quote because saline water does not exhibit the 4oC maximumdensity anomily like fresh. See fig 3.1 here http://www-pord.ucsd.edu/~ltalley/sio210/DPO/TALLEY_9780750645522_chapter3.pdf