studiot

For elementary kinematics (involving only constant acceleration) there are not many formulae v2 = u2 + 2as v = u + at s= ut+ 1/2 (at2) a = (v-u)/t s = 1/2(v+u)t Do you know these?

You would need to be about 70 kilometres up in the sky for the acceleration due to gravity to be 9.6 m per second2 The standard value is 9.81 ms-2 Often you can use 10 as a good enough approximation. Using this in the formula provided by ajb final speed = sqrt (2 x 10 x 400) m/s = sqrt(8000) = 89.5 m/sc When you do science it is vitally important that you get you physics facts and your arithmetic correct.

I'm not quite sure why the OP has not returned since posting and the collection of replies are pretty helpful. However there is one missing fact. It is not strictly true to say that light does not pass through a concrete (or any other) wall. For any material there is what is known as the attenuation coefficient. http://en.wikipedia.org/wiki/Attenuation_coefficient All radiation, including non wave particles like alpha and beta and sound, the attenuation of the radiation depends upon the thickness of the obstacle. For most materials this is a non linear exponential relationship with a 'half thickness' similar in concept to the half life of radioactive substances. This 'half thickness' is the thickness that will reduce the radiation by 50%. The difference between coefficients for different materials and for differents forms of radiation is due to the specific differences in the interaction between the radiation and the material, as others have noted.

x must be real by the OP's own (conventional) notation.

Well you could try anywhere and use artificial soil.

Can you tell me how the sin of something plus the cos of something else will ever add up to 4, whether you take the square root or not? Or are you just extracting the Michael?

In all honesty this is a bit vague. Do you have any specific areas of interest or goals as to what career you might like to follow? Having a goal is pretty important. You can focus on it rather than on the people around you when things get difficult and distracting. Others here are right, chat forums are not the place for formal courses, but many have found great help by politeness and cooperation. So ask away, you can already see that others here will help when you are open and honest about your intentions, like you have been.

IMHO we are all being unfair to General Dadmission. The question posed is a very good one and as clear as the general physicists's answer, since physicists cannot agree amongst themselves as to the nature of mass. Just look here. http://en.wikipedia.org/wiki/Mass_in_general_relativity On the other hand, both sides of this discussion need to be even tempered for it to be fruitful. General Dadmission, if someone does not understand your words or finds them unclear, what is the practical way to proceed, since you are asking the question and presumably want the answer. I do not claim to be sufficiently well versed in modern and theortical physics to supply an answer but would like to set this in context. What I think you are asking about has puzzled physicists since Newton, who first realised that there are two effects in nature that we call mass. In Newton's day they reconciled Force = mass times acceleration and the the gravitational law. It is interesting that inertial mass and gravitational mass can be shown to be equivalent in classical systems, although it took approximately two hundred years to fully work this out. To put this in context, Physics has achieved several major successes in combining effects, once thought separate, the timescale in each case being one to two hundred years. For instance up to the 18th century they though heat and work were separate effects. Enough history. General Dadmission, I am wondering if your question is equivalent to Does the apparent increase in mass due to relativity show up as an increased gravitational force? Over to you for a fruitful and respectful discussion.

+1bob, this is oft forgot.

http://forum.allaboutcircuits.com/threads/bicycle-path-geometry.107435/

Please remember that the OP has set the question here. In particular the OP has distinguished between movement (or lack of it) and acceleration (or lack of it). Movement is a more general term that does not imply velocity. I think the question may well be along the lines of the old saw, often called the riddle of the Sphinx. "What has four legs, two legs and three legs?" That is why it is called a brainteaser - it calls for thinking outside the box.

Hello again simina, have you abandoned Science Forums? I left the question for Enthalpy to complete with you, as is seemed particularly apt from the zero enthalpy condition. But since no one else has added more here are my thoughts. Firstly you need to be much more careful about careless errors, you have two in this question, this is a pity because you are on the right track. Why would this be? You need to check your maths more carefully, where did you get the equation from? [math]\int\limits_{{h_1}}^{{h_2}} {dh} = \int\limits_{{T_1}}^{{T_2}} {{C_p}dT} + \int\limits_{{P_1}}^{{P_2}} {\left[ {V - T{{\left( {\frac{{\partial V}}{{\partial T}}} \right)}_P}} \right]} dP[/math] Which you have correct. But then you are too quick in your substitution from your equation of state. Yes the R/P terms 'cancel' (though I don't like this word like this) but that does not destroy the equation when you integrate. Thus [math]V = \frac{{RT}}{P} + b[/math] and [math]{\left( {\frac{{\partial V}}{{\partial T}}} \right)_P} = \frac{R}{P}[/math] Substituting [math]\int\limits_{{h_1}}^{{h_2}} {dh} = \int\limits_{{T_1}}^{{T_2}} {{C_p}dT} + \int\limits_{{P_1}}^{{P_2}} {\left[ {\frac{{RT}}{P} + b - T\frac{R}{P}} \right]} dP[/math] So all three intergral terms still exist, therefore performing the integration [math]\int\limits_{{h_1}}^{{h_2}} {dh} = \int\limits_{{T_1}}^{{T_2}} {{C_p}dT} + \int\limits_{{P_1}}^{{P_2}} {\left[ { + b} \right]} dP[/math] [math]\Delta h = 0 = {C_p}\Delta T + b\Delta P[/math] rearranging [math]\Delta T = - \frac{b}{{{C_p}}}\Delta P[/math] Now care is needed at this point because deltaP is negative here therefore deltaT is positive, which is correct since the Helium is above its inversion temperature. Someone has mistranscribed the value of b by a factor of 1010! b should be 2.3 -5x10, not 2.3 x 105 as you had it. (don't you think the forum superscipt and subscript is better than the carat ^ symbol?) When you put these values into the final equation you get a resonable answer for the temperature increase of the Helium. Further care is needed as tio the value of R employed. Do we mean the engineer's R (the universal gas constat divided by the molar mass) or the universal constant itself? I will leave you to ponder this one.

Forums usually end up being whatever the members make of it, despite the rules, which are usually just a version of common sense and common politeness. Like ajb, your subject headings have not interested me so I have not been following them, but your post in this thread makes me wonder if you are scientifically trying to run before you can walk. In the words of Moontanman's people, "Tread softly on the mountain."

Fared, you are getting adverse responses because you are not helping others to help you. You say this is postgraduate research, but haven't given any indication of what research. So folks are just guessing. At postgraduate level I would expect the statement "The temperature dependence of blood surface tension" to be much better qualified. For instance blood? What sort of blood?, are you going to compare blood from different species, making more sense of the different temperatures? What about the age of the blood? The physical properties of stored stored human blood changes with length of storage, there is already published rersearch about this in respect of IV pumps. So set your stall out properly.

Acceleration is frame dependent. The geodesic travelled by a photon has zero acceleration in velocity or direction. Edit Actually John, thinking about it, I do believe you are right and photons don't count since they can be stopped by absorption, which must be the utlimate deceleration. So instead I observe that I can move a decimal point, but I can't accelerate one.

The equation says The modulus of the expression = 1. The modulus is a real number, what is the expression for it in terms of x and y? What is the locus of all point in the x - y plane whose modulus is 1? You should be able to plot expressions ax+by = 1 on the xy plane; What does that plot look like? Let the complex quotient in the expression be equal to [math]\alpha x + \beta iy[/math] Then reduce the quotient to this form and equate coefficients; Do you know how to reduce a complex quotient to a single complex number (ie bring the complex part from the bottom to the top) ?

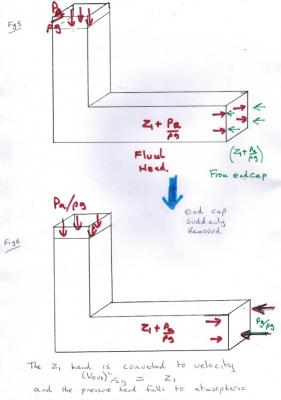
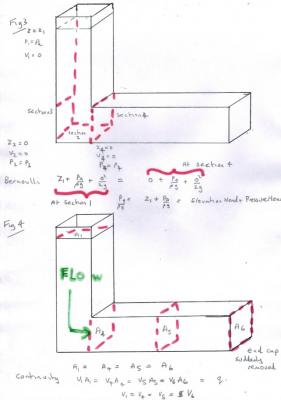
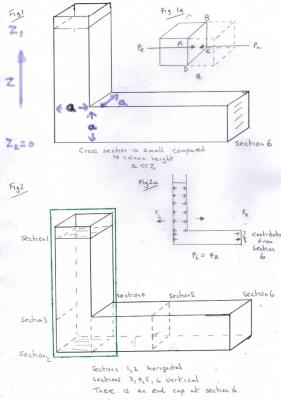
So the purpose of the collection was to look at zet's post83 'experiment'. It is suprising what can be deduced from a simple static situation in the bent tube. Zet is right to try to simplify, but it takes experience to know what can be left out and what must be included and the idea is to examine this as we go along. I have drawn a square tube of side 'a', since flat surfaces are easy to work with and section area calcuations are simple. The initial setup is shown in Fig1 with elevation (z) reckoned upwards from the base of the horizontal part of the tube. The tube is shown as constant cross section,a x a where a is small compared to the height of the fluid level in the vertical column. This allows a simple representation of the fluid pressure in the lower horizontal part of the tube as the pressure at z=0. Talking of pressure it is worth noting what is meant by 'fluid pressure' and I have inset Fig1a to show this. Consider a small cube within the fluid, shown solid. This cube has a face ABCD on which the cube exerts a fluid pressure PR as shown. The fluid in the adjacent cube, shown dashed, must push back with an equal and opposite pressure PL, or the cube would move. This must, of course be true of the other five faces of the cube. If the face of the cube is against a container, not more fluid, then the container, must supply this pressure instead. These can also be cast in terms of Newton's 3rd law, using force instead of pressure. I will return to these comments later. Now that we have our tube set up, but capped off at section 6 so the fluid can't flow out. To start with let us examine the flow without the airfoil and introduce it later at section 5. Our control volume is from section 1 to section 2, as shown in the green box in Fig2. Since the column is vertical these sections are horizontal. Section 1 is the top free surface of the fluid. The pressure here is atmospheric. In the inset in Fig2a I have returned to my earlier point about the pressure on the walls of the container. The forces to the left (FL) must be equal and opposite to the forces to the right (FR) or again the whole container will move. Again since the fluid is pressing on the container, the container pushes back equally. This may be stating the obvious, but it will become important, along with momentum later. This now leads to Fig3 and a Bernoulli analysis at sections 1 and 2. This is where working in terms of head comes into its own. There are three terms in the simple Bernoulli equation I called equation 1 in post146. At section1 the elevation head is simply z1 Since the velocity is zero the velocity head is zero And the pressure is the ambient (atmospheric) pressure at the free surface. At section 2 The velocity head is still zero The elevation head is now zero, since z2=0 and the pressure head has therefore increased. I have shown this in the equation although I have used vertical section 4 to save a drawing (Remember I said keep 'a' small so we can consider the pressure the same over the whole of vertical sections) This enables us to calculate the pressure along the whole of the horizontal section of fluid. If we now suddenly remove the end cap at section 6 so the fluid flows out, as shown in Fig4. Fig 4 is also about the law of conservation of mass and continuity. Since our fluid is incompressible the same quantity of fluid that flows aout through section 6 must also flow through each other section as shown in red. But since all the sections have the same cross section this means that the velocity has constant magnitude throughout the fluid. If we change thearea at section 5 by introducing the airfoil we must change the velocity to compensate. Unless we know the volumetric flow rate we cannot calculate this changed velocity at section 5 to put into Bernoulli. Fig 5 returns to the static situation before endcap removal for a bit more analysis. Note clearly that the velocity here is zero throughout the fluid. Therefore the momentum is zero throughout the fluid. This comment is important to the airfloil lift, which see the same mechanism about to be discussed, in relation to momentum. I showed in inset Fig 2a that the pressures and forces on the walls of the container balance, and that the wall supply a reaction to the fluid. If we suddenly remove part of those walls in the form of the cap at section 6 we must also remove that reaction. We replace that reaction with the ambient (atmospheric) pressure Pa This explains why the fluid starts to move. The fluid is still at pressure head of (z1 + Pa/rhog) whilst this is opposed by Pa/rhog alone. So the driving head is the difference, z1, as shown inf Fig 6, which allows us to calculate the starting exit velocity of the fluid. Before the cap is removed there is zero momentum. After removal the fluid possesses momentum to the right. So there must be some equal and opposite momentum to the left, because momentum is a conserved quantity. The rate of change of momentum constitutes a force and this force acts on vertical section 3 of the container, pushing it back of the left. This is, of course, how a rocket works. The changes that occur as the level falls require calculus to address and I will leave to a possible later post, along with the application of the Work equation, I have called equation 3, in post 146 to estimating the head loss due to the airfoil. Hopefully this is enough to convince you that because of the interaction with the container walls the analysis of contained fluids is different from that of a semi infinite fluid like an atmosphere. However it is always encouraging when Newton's laws, conservation laws and any specialist laws applicable to the subject in hand, all offer the same answer and fit together nicely.

One of the properties of infinity is adding any real number to it still makes infinity, or if you like subtracting any real number still makes infinity. Neither of these are properties of (9recurring).

Of course not. Is infinity a constant? What does adding 100 to infinity make? is (9recurring ) + 100 = (9recurring) ? Infinity is not a real number or an integer, 9 recurring is and obey all the rules of integers and ral numbers. There are number systems which include an infinity, but not the real numbers or the integers.

I asked my [insert] favourite politician [/insert] this one, The reply was Rename them Walter currents.

I think I originally misunderstood you. Why will taking the log(77.960603) and subtracting log(37.960603) and then taking the antilog not give your answer?

Have you ever tried telling the corporate IT environment that you want permission to install a particular program, not on their list?

What is 20 the log of? and what is 3.873 the log of? And what is the log of A added to the log of B the log of?

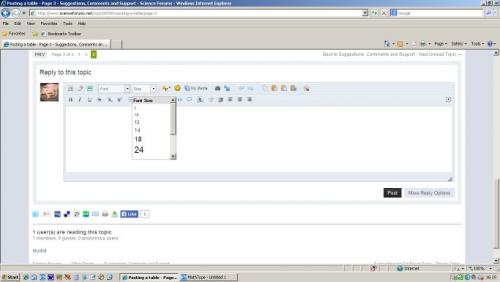
Here is the result of (left) clicking once near the top of the "big empty box". In this case it opens with the font size selector selected, but it could be any of the random options available.