studiot

[math]v = \frac{1}{{2\pi }}\frac{{\sqrt {{k_f}} }}{m}[/math] cross multiply [math]2\pi mv = \sqrt {{k_f}} [/math] square both sides [math]{\left( {2\pi mv} \right)^2} = {k_f}[/math] can you complete it now?

Yes that's the size of it, but remember that the solutions not only satisfy the equation but also the boundary conditions. There are many more solutions that satisfy the equation, but not the boundary conditions.

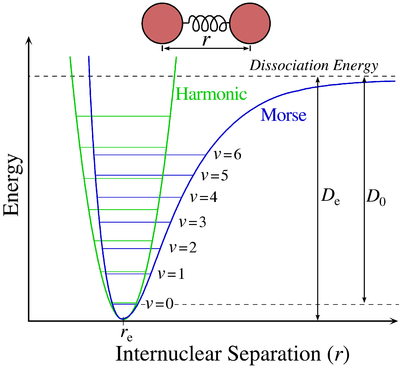
The Schrodinger equation can be writtern in terms of the Hamilton operator H(_) and the total energy operator E(_). [math]H(\psi ) = E(\psi )[/math] Now this is a partial differential equation that has functions as solutions. So any solution, [math]\psi [/math], is a function of the space variables in the original equation. As with any differential equation we pick out desired solutions by imposing boundary conditions. If these boundary conditions lead to a set of solutions only for discrete, separated values of E, that is they constrain E only to certain specific values (remember E is a scalar) then the solutions are called 'eignefunctions' and the values the 'eigenvalues'. Some boundary conditions, however, allow solutions, [math]\psi [/math], that can take any value of E (perhaps within certain min and max limitis). In this case there is a continuous spectrum and the solutions are not eigenfunctions. So if we take the so called Morse energy curve for a quantum oscillator (from Wikipedia) We see two regions in the graph. The Schrodinger equation applies to both parts. The lower part shows discrete separate energy levels getting closer together as we rise up the vertical axis, until there is a second region labelled 'dissociation energy' and a continuous emitted spectrum. The energy levels in the lower region correspond to eigensolutions. The continuous range of allowable energies in the upper region correspond to non eigensolutions.

Gosh what a silly question to set. So many variables (questions that could be asked) and such narrow categories. Are any of these categories measured against a scale? Characterisation: Is this situation a red emergency? amber? or just a warning? Just humans? Is is getting better? Is it a one off? Fundamental: Route? When? For how long? Could any more come this way? Any other sources?

I haven't checked the arithmetic but your figures are the right sides of the value I got for a 2" pipe. However do you not think your value for the 1.5" pipe is telling you that that flowrate is impractical for such a pipe?

A 2" pipe has a 1" radius and 1" is 1/12 feet, yes?

Well I found it really intriguing and thought provoking, once I got the hang of it, which was not until the first time through was nearly complete. I thought the technique employed art well, if subtly. I have a pre-computer age manual of such presentation techniques. However I don't think the quoted target audience would have the patience to make that effort. The one person I showed it to, has several degrees up to Msc and found it difficult to follow without explanation.

Try the arithmetic again. 500 cfm = 500 x 60 cuft/hour = 30,000 cfh v = 30000/(pi x (1/12)2) =ft per hour divide this by 5280 to get to mph.

Unusual presentation. Would this be an example of what MikeSmithCosmos called Art in Science?

Within limits, yes. If you tried to force the air into too small a pipe, say 1/16", you would probably not be able to do it - the resistance would be too great. And if you opened out the pipe too far. say 72", it would become a chamber and air would start to circulate as in the atmosphere.

You cannot change the volumetric flow rate (cuft/min) by changing the pipe size or air would accumulate somewhere (or worse appear out of nowhere). The volumetric flow rate Q = Area cross section times the velocity. Note for your units the area is in square feet and the velocity in ft/min. Your second question, what is the diameter change from a 2" pipe to a 3" pipe is surely (3"- 2") = 1"? You cannot calculate the flow within the adapter or about 3 diameters upstream or downstream by these methods.

[math]\Delta \Phi [/math] = [math]\frac{{2\tan \theta }}{L}[/math] Where delta_phi is the pipe diameter change, theta the flare angle of the adapter and L the pneumatic length of the adapter. Is this what you really want or would you like to explain your needs further?

Cu + 4HNO3 = Cu(NO3)2 + 2H2O + 2NO2

Are you studying the method of redox half reactions? These are balanced by adding electrons. Some multiples of two half reactions are added to create a full chemical reaction equation and the electrons cancel out. http://www.chemguide.co.uk/inorganic/redox/equations.html

In this thread someone quoted entropy. Now there are many confusing ways to introduce entropy, but I found the easiest was the traditional path of indicator diagrams. A function along an axis was found to be useful and given a name. In the case of entropy the desired function was one that paired with temperature to give the dimensions of energy (as an integral on the diagram), in the same way that the intergral of a pressure-volume diagram give energy. In this recent question here about the nature of time I offered a similar route to time as the label for an axis that was required to perform an analysis. See post#62 http://www.scienceforums.net/topic/82939-explanation-of-time/page-4

So what is your definition of information?

Well I'm all ears since I could do with a proper definition of Time. But lighten up as well. Poul was renouned for getting his science right, as he did in the book I mentioned. The story was obviously a fairy tale, but IMHO he wrote some cracking ones.

If you are also experimenting with radar/microwaves please, please remove any rings, watches with metal straps or any complete circles of metal. I know of at least one engineer who lost a finger becuase of this. go well

All this is really science fiction. In that respect Poul Andersons's book 'Tau Zero' is as good as any, and better than most.

Every isolated thermodynamic system................ The problem with applying this to the Universe is that we have no proof that the universe is an isolated system (or that it is not, we just don't know) in the thermodynamic sense.

Since you ask so nicely English is made up of words. Since words are imaginary and you declare (again so nicely) that anything imaginary doesn't exist, English doesn't exist.

Really Sam, I'm disappointed. I thought your counterarguments would be better than this. Discussion like this is just an insulting waste of time. I didn't say anything of the sort. Of course it is easy to change what someone said to attempt to falsify their assertion. If you wish to dispense with English, the official language of this forum, there is nothing more we can discuss. Nouns are, of course, a very precisely defined part of English. Since post#5, I have been offering the suggestion that misunderstanding and/or miscommunication has arisen because some folks mistakenly identify the meaning of the English word 'real' with the requirement that only concrete noun represent reality. This is of course not true but since you eschew English itself how can we discuss whether anything is 'real' or not?

Second thoughts.

No not at all. Phase methods were popular before precise timing became possible. Think names like Loran, Decca, Tellurometer Interference methods were also used, think Geodimeter. and the NPL one whose name I can't remember. But we need proper specification from the OP.

There is at least one other way, that I referred to in post#4 than time of flight measurements. These do indeed work around corners and obstacles, but introduce different issues. I was waiting for a better description of the problem from the OP.