studiot

Is the following quote not true? You are clearly stating that you do not understand Pauli, or know what he actually said, yet you introduce hearsay to support your (scientific?) assertions in this thread. This is, of course, not accepted by any of the many models in mainstream physics. If you had a Maxwellian Daemon that could effect a switch of the two atoms, you (or anyone else) would not be able to tell the difference. That tenet is one of the most fundamental in physics.

You are still avoiding the issues that you yourself raised. Unique? In what way? Take an atom of copper in Rio de Janeiro and compare with another one in Adelaide. Are they unique? Does Pauli make them unique or prohibit them from having the same 'state'? Observation? What observation?

Well geometry is a very wide subject that has developed considerably in the nearly two and half thousand years since Euclid. It is this development that has muddied the waters somewhat in the distinction, since in Euclid's day there was only one sort of geometry, some of which we no longer include in modern definitions of 'Euclidian Geometry'. To distinguish I offer a description of modern Euclidian Geometry. Any other sort of Geometry is non-Euclidian. The main characteristic feature of modern Euclidian Geometry is the idea that the distance between two points is given by the square root of the sum of the squares of the coordinate distances between them. In other words the scale factor is the same in all directions at all points in the region of interest. This is not true for instance in Projective Geometry used by artists for perspective and cartographers for mapping, and draftsmen for some aspects of engineering drawing. It is also not true in the Geometry of most surfaces, particularly spheres. One consequence of this property of Euclidian Geometry is that it aligns with what we now call Vector Geometry. That is we can prove theorems in Vector Geometry by Euclid or vice versa. Vector Geometry is itself a development of Coordinate Geometry. So Coordinate Geometry is Euclidian. We now identify Euclidian Geometry with what we call linear algebra and vector spaces. Another form of Geometry involves the application of the Calculus to Geometry. Euclid did not know about the calculus and this sort, called Differential Geometry, has some Euclidian and some non Euclidian aspects.

So what is the question?

So I'm wasting my time discussing with you then? You are the one who introduced the Pauli Exclusion Principle to this thread. (post#14) The PEP concerns some quantites that include time in their definition. Period. You cannot have it both ways.

I agree that that on first reading something appears amiss. What is a lake? That is does it include the container for the water or is it just the water? A good way to be clear is to specify "the water in the lake is likely to suffer.........."

@ Fred Champion A gently nudge towards post#39

For those who think they know what would happen to something travelling faster than light it is instructive to put v>c into the equations. The problem occurs at v=c since relativistic expressions involving the ratio [math]\left( {\frac{v}{c}} \right)[/math] result in an attempt to divide by zero. This is not the case when v<c or v>c, although the results of the latter calculations are interesting.

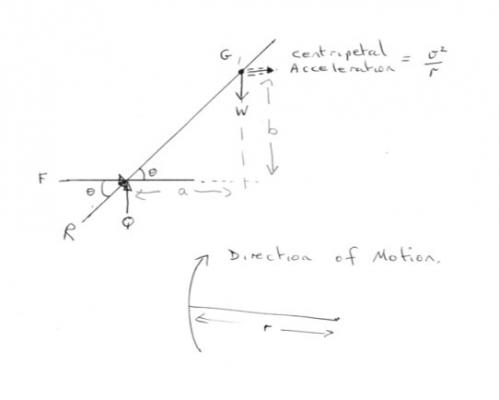
From what you say, this is not really a homework question. So I can post a more complete answer. I think you are trying to make the issue too complicated by concentrating on the patch of contact between the tyre and the road. The crux of the analysis is that the reaction between the tyre and the road has to pass through the centre of gravity of the bike or it would fall over. Consider a bike plus rider, of weight W, travelling around a horizontal curve or radius r as shown with velocity v. It is subject to a centripetal acceleration v2/r There is one point (or line) of contact with the road, so the total reaction here R, is comprised of the vertical reaction, Q and the frictional force F. F is the only force that can supply the horizontal centripetal force necessary to exert the centripetal acceleration, thus [math]F = \frac{W}{g}\frac{{{v^2}}}{r}[/math] If the cyclist leans over at an angle theta the line from the point of contact with the road must pass through the centre of gravity, so R must pass through the centre of gravity, G. (W passes through G and also has no moment about it) Further since there is zero vertical movement [math]Q = W[/math] So [math]\tan (\theta ) = \frac{Q}{F} = \frac{W}{F}[/math] The analysis of four wheeled vehicles is different.

No I don't think you do now either. I was and still am (gently) challenging your understanding of the Pauli exclusion principle, I offered further detail by noting that the PEP only applies to fermions. The above was extracted from http://en.wikipedia.org/wiki/Boson Why not? If what do you understand by state? I understand it to be a list of parameters, some of which are a function of a physical variable we call time. Without this variable the parameters themselves would not exist so how could the state based on them exist? For instance two of the parameters in Pauli's list are angular momentuma and spin. Both are the time rate of change of something.

Yeah, that's true. I was trying to establish some context before answering your 3 specific questions. I don't know how much you know but the subject of wave motion takes up whole chapters of physics or applied maths texts at every level from elementary to postgraduate. There are even complete books about it. The particles do not form the wave. Notice I said that the elements or particles 'carry' the wave. A wave is not like traffic on a road. The traffic is made up (formed) from lots of individual vehicles. This is the first and most fundamental thing to know about waves, nothing else will make sense until you have understood this point. Imagine a single weight hung on a spring bouncing up and down. That is a single oscillator or vibrating element or 'particle'. It is not a wave, and not executing wave motion. Now suppose we have a bunch of similar weights on springs. They could be made to bounce up and down completely randomly, with no connection to each other. That is still not a wave. But suppose that they have a mechanical connection so each weight will nudge its neighbour and impart some of its motion. A wave is then formed that passes down the line of weights as the motion is handed on from weight to weight, like a chain of buckets. But the weights themselves do not move along the line. I can draw a sketch later if that helps.

Agreed the 't' test would be appropriate. Unity, since you are doing so well, perhaps you would like to explain about samples and populations since the object of the exercise is to compare populations by comparing samples from different clam populations. A question for bluebird Do you think this should be a one tailed test or a two tailed test?

You need to distinguish carefully between the wave and the vibrating particles or elements carrying that wave. The motion of any wave is not the same as the motion of the particles. The speed of any wave is independent of the speed of the source. This includes the speed of light waves however light wave are unique in that the their speed is also independent of the speed of the observer. A medium is an array of linked vibrating particles. Once a wave has left the source and is being transmitted by the medium its speed is normally a constant determined by the physical properties of the medium.

This is a very long term discussion, with one post per week or so. Do you only have limited internet access? Or do you have to translate replies? I don't fully understand what course you are studying. The folk classification is for a particular groups of sedimentary rocks, not sediments themselves. What you have posted is more like a soil classification. Are you studying the rocks or the sediments? For what purpose? Here is a good resource, it includes answers to your question about measurement. Post again if you want more. http://environment.uwe.ac.uk/geocal/SoilMech/classification/default.htm

I was looking for a sketch.

Sure, but it makes a good movie eh?

Earthquake effects do not work like this. The Quake is a travelling wave. This means that is has a wavefront. This is a sharply defined section. One side of the wave is doing one thing (perhaps going up) The other side is doing something else (perhaps going down) This is called differential movement. So as the wavefront passes through the building, different parts of the structure can be moving in opposite directions. This snaps floor slabs, pushes up sidewalls and detaches them and much more. Unless the building is very tiny ( and therefore probably safe) the quake wave does not affect the whole building at once. That is the point.

Not really. soil mechanics is quite a specialist (and technical) subject. I can do the fancy maths if you prefer.

I'm trying to be as explicit as I can. If the P wave 'shakes up' the soil then it may loose it's strength, like the ketchup. This was only condition 1 on my list. Condition 2 is different again. The weight of soil (as with anything ) is w =mg. That is the mass times the acceleration due to gravity. Usually this is the only force acting on the soil. But if there is an acceleration due to the P wave then a second force is applied. This may be sufficient to make a previously stable bank of soil unstable.

Sorry but I didn't say that either. What happens when you shake a bottle of tomato ketchup?

So am I What does all this stuff have to do with the original post?

Sure thing, I am happy to discuss further if you wish.

I didn't say any of that, read it again. The P wave affect the foundation earth material. rather than the building. PS do you understand that 'foundation' refers to the earth or ground supporting the structure, not the structure itself?

S waves cause actual differential movement of parts of a structure. If this cannot be accomodated by the structure, it will fail. P waves alter the characteristics of the foundation earth material, due to the accelerations involved in the wave. This has two effects. Firstly it can cause the foundation material to loose some bearing capacity, and therefore the ability to support all or part of a structure. Secondly all loaded foundations have failure planes and other surfaces (eg the slip circle) which are loaded by the earth above and any structure on that superficial earth. The acceleration of this material increases the force on it, because force = mass x acceleration. This can take it outside the support range of the plane or circle (in shear), causing failure of the earth. This applies in particular to cutting sides and embankments.

Fred Champion The point was (is) that the state of an object provides no link to any sort of deduction about time. The formal statement of Pauli that I have seen does not include "at the same time", or any other reference to time, because a reference to time is neither necessary nor proper. In order for the state of an object to link to time it would have to include the recognition of some sort of change (velocity, momentum,etc) and change is recognized only over two or more states. A correct description of state will include only one state (the one described) and not others. The state of an object is much like the photo of a clock. While a series of such photos may imply an intelligence (with the necessary memory) capable of recognizing change, it does not imply any phenomenon beyond that, and a single photo of a clock provides no indication of change at all. You have not addressed my question, which was quite specific. The complete wavefunction describing a many particle state is antisymmetric under the exchange of any pair of identical fermions and symmetric under the exchange of any pair of identical bosons. So first of all only fermions follow the Pauli exclusion principle, which follows directly from the above statement. Secondly, the Exclusion Principle that no two identical fermions (from the same system) can have the same set of quantum numbers, applies throughout time. That is why time is not mentioned. Because it can never happen. None of the foregoing prevents interpenetration, which is another name for quantum tunnelling, upon which the computer I am writing this depends for its action.