studiot

Consider the wave defined by [math]\zeta[/math] = [math]A\sin (\omega t - \varphi )[/math] The phase is defined to be the value of [math]\varphi [/math]

I have no idea what you mean by either of those statements.

What you say is true, but not relevent since the experiment I described did not present that condition. Yes, of course you can, the signal is then different. What does that have to do with the case in point? So I look forward to your prediction about the results I am now measuring.

Thank you , Lizzie. I did try bicarb/vinegar but it had no effect (except for the fizz).

Thank you for your comments. 1) Phase. Try the following experiment. Take a loudspeaker and listen to it. Now reverse the connections. Can you hear any difference, the phase between the two connections is as far apart as possible? You can also do this with a pair of loadspeakers, with the same result. 2) I agree, the ear is a complicated sound receiver with many signal processing and conditions features. 3) I have yet to see any of the multitude of those claiming the measurable difference to offer anything other than hand waving statements in support of their claim. Nor have I seen anyone else prepared to make experiments or measurements. I have offered both measurements and solid mathematics that results in the same values as measured. When I read the OP I had not come across this effect so I experimentally confirmed it for myself. Since it is interesting I have not yet finished and yesterday received a real time audio spectrum analyser with a much finer pickup than my own meter. Preliminary results have confirmed the overpressure levels, but produced one suprise so far. I have not had a chance to complete the measurments yet so will hold off reporting more detail until I have proper data. This is taking some time as I must refresh my technique on this kit as I last used it a couple of years ago when doing some consultancy audio work on the noise of rotary aero engines. Unfortunately I have not yet gained any access to accelerometers or vibration monitors to detect the actual frequency my "bell" is vibrating at - I can only test the sound in the air. A really good challenge for alternative theories is "Can they predict what this suprise is in the new measurements"

I didn't dare try acetone as it dissolves or softens too many plastics or, almost as bad, the plasticiser in some harder plastic. I think the wellies are pvc of some sort.

Well I, for one, don't understand the coloured blocks or what you are saying about them Lizzie. What should I be seeing on these blocks?

Agreed. But there is much more to this since even after a law is passed it and its effects are not certain until substantial case law has been established. There is always room for another side to argue a case and sometimes they prevail. What for instance if you click on a link, that has been maliciously altered, believing it to be one thing, only to find you have downloaded soemthing entirely different? In the UK I know of no cases where someone has inadvertantly clicked on a single link and downloaded one thing and gone no further. Al the reported cases are about individuals who have systematically downloaded large numbers of files and then proceeded to sell them for profit. But there are still caveats. It has also been held that if you are in an East London pub one dark night and some stranger offers you a £2000 Rolex watch for £20 you should be suspicious.

imatfaal is the guy to elaborate on what I will now say but the UK is an occasional member of the EU as well. However the Uk law stems from vastly different roots than the Napoleonic code. In particular we have different civil and criminal codes. To be against the criminal code an act must not only be performed it must be perfomed with the intention to commit a criminal act, or soemtimes in criminal negligance. I do not think that inadvertantly clicking on something without realising a criminal content could be construed as criminal intent. I look forward to inmatfaal's comments.

Well, difficult to suggest specific titles without knowing what level, as ajb says. However on a more general note, although you are not studying a formal course at school (and presumably not going for an exam) school textbooks offer a balanced presentation of the subject at a common level so are better than targeted or single subject books. Popsci books in particular are designed to push a particular message. You often require combined input from several differnt parts of the subject to understand a point. For example to properly understand the working of your electric fire you need input from the mechanics and heat (thermodymics) branches of physics as well. Since you are not following a formal course, you do not need the latest textbook, so you can pick up older editions or older books for very little from second hand sources. these will be perfectly adequate for your needs. In a school environment you would also learn associated subjects (mathematics and perhaps chemistry) in parallel with physics, most physics books will assume this so will be deficient in this area. If you looked at what tech colleges call "engineering science" you might find more useful material. Engineering science is basically less mathematical physics with a smattering of chemistry and is more down to earth so easier to digest on one's own. Good luck in your personal studies.

A bit like castor oil into the ears of small children? Thanks for the thought. I did try elbow grease in the form of various brushes on the end of a modellers drill. Not really a huge success. Finally got it all out by soaking in cellulose paint thinner (composition not stated, but the Lidl cheap one worked better than the glassit proprietary one "contains toluene") and scraping with a toolmakers small cleaning kit of scrapers and brushes. I am just left with a stain in the bottom, which is acceptable. Please note that if anyone is thinking of using these techniques, I do this in the open air on a concrete slab fore safety reasons. Thanks all for your thoughts.

White sheets of paper, white bedsheets, white sheets of plastic, the situation is the same and you can compare. White bodies reflect all wavelenghts of visible light. Coloured bodies remove some of the wavelengths so the colour you see is what is left and reflected. The difference between a mirror, which also reflects all wavelenghts and a white body is that mirror reflection is called specular reflection. The surface of a mirror is smooth at the microscopic dimension sizes of light wavelengths, the surface of a white body is rough. This means that the light from a mirror reflects in an organised fashion, whereas the light form a white body bounces off in random directions. https://www.google.co.uk/images?hl=en-GB&q=specular+reflection&gbv=2&sa=X&oi=image_result_group&ei=I0lGU5OBK8rdPauFgLAM&ved=0CC4QsAQ

Go visit these people, look at their website, get their literature, join up. http://www.ima.org.uk/

I'm sorry I don't follow this. These are these are all calculable (which means I get these answers) from the information given. I would say a calculation scheme would run like this, parts (a) and (b) being to calculate the velocity of the ball at impact and the velocity of the ball and block immediately after impact. 1) Calculate the velocity of the ball at impact by equating the potential energy gained from its fall from its release position to the kinetic energy it has at impact. This does indeed yield 7m/s. 2) We may then obtain the post impact velocities of both ball and block from conservation of both energy and momentum simultaneously. This yields -2.33m/s for the rebounding ball and 4.66m/s for the block. Notice the negative sign on the velocity of the ball. 3) The force of static friction does no work. So no kinetic energy is lost overcoming static friction. This is why Ron's answer is correct. The KE acquired by the block from the ball is given by using the immediate post impact velocity of the block in the usual expression for KE. 4) The block moves a distance d against the constant resistance, R, of kinetic friction. This therefore does do work, dissipating the KE of the block in distance d, therefore doing Rd joules of work. Equating this to the KE of the block plus should yield d.

Since you like exhibitions another good one is the home of photography, the Fox Talbot Museum https://www.nationaltrust.org.uk/lacock/ Also worth a visit is Futuroscope in central France the Museum of the Moving Image http://en.futuroscope.com/ And there is a museum in that is in the making inYorkshire concerning the recently discovered pioneer of moving images. Sorry there is no link for that yet.

Continuing the theme of Art in Science Who has seen the BodyWorlds exhibition? Highly recommended, but is is Art or Science? http://www.life.org.uk/whats-on/body-worlds

I am trying to keep this discussion friendly. I think we are agreed on the merits and demerits of the problem in hand. It's just in the presentation we can surely agree to differ. Unity+ can then have the (luxury) of two different points of view to choose from. He is a first rate student and I have a lot of confidence in him. I didn't say otherwise, however since you ask I believe it's called fluid pressure. A vertical force (acceleration) due to gravity becomes a horizontal force (acceleration) within the fluid. It is also true to a less obvious extent that in solids a vertical force (due to gravity) becomes a horizontal shear force.

How can you say that? Are you not considering it by saying it does not work? All I have asked for is sufficient justification to exclude it. I was taught to start static analyses with the words "As in equilibrium." At the tiem I thought "what an unnecessary fuss. But the number of poster I have seen here here carrying out inappropriate equilibrium analyses on systems that are not in equilibrium justifies it in my hindsight. You have also talked about gaining extra marks for a good discussion. You can also earn extra marks (or at least prevent loss of marks) by justification statements so even if (as here) the strain energy calculation went awry the statement Total energy of system = Strain energy + Potential Energy + Kinetic Energy = A constant Would earn part (or even half) marks. And in the real world outside proper annotation and documentation can help understand the flow some time alter.

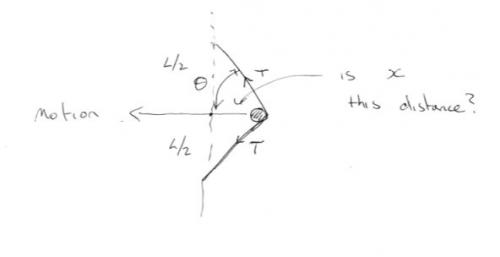
It's not unnecessary in this case since the original analysis was flawed. Further this analysis is also suspect What is x? I have already said we need a diagram. How many elastic forces are acting on the ball? In my diagram the orientation could be vertical, in which case there are opposing vertical forces to consider It could be horizontal or somewhere in between. It then becomes necessary to prove that there is no exchange of energy between horizontal and vertically acting agents. See my comment on the pendulum at the end. I also am not sure what the dimension x represents, because if it is as I have shown then it is not the elastic extension of the band. As to conservation of energy and resolution into components. I do not think for one minute that I have anywhere implied you cannot or should not resolve vectors including forces. My intention, since it is an important technique, has always been quite the reverse. I' ve tried to carefully avoid say horizontal or vertical energy, rather to indicate what may be correctly attributed (resolved) into such directions. If you consider the humble pendulum and gaily state that you may gaily separate the energies into horizontal and vertical you will come to inappropriate conclusions. The total (mechanical) energy is constant. In the centre of the swing it is all KE and the motion is purely horizontal. At the ends of the swing it is all PE and the motion is purely vertical. Everywhere else it is some combination of both. So there is an example mechanical system where gravitational PE and the energy due to horizontal motion are interchanged.

Reading my previous post I realise you might I thought I was inviting comments on JC, so I apologise for the sloppy posting. I meant that was the start of my comments on the physics of the question. Conservation of energy (from which the balance equation is derived) applies to the total energy. You cannot just take a bit of the system's energy and equate it to another bit. Just taking the "horizontal energy" implies we can resolve energy into components, which is not true. Any of the energies can be converted to any of the others, given the right circumstances. If we do ignore some energy we should always show why; for instance there are no magnetic forces acting, or if we can say that a particular energy is constant, we can ignore it. Neither the gravitational PE nor the kinetic energy due vertical motion are contant. Similarly the calculation of the time of flight stems from the constant acceleration equation s=ut+0.5ft2 Had the zero term been included here the nonzero term in the energy balance might not have been missed. This may be considered a philosophical point or excessively pedantic, but many questions are fluffed simply due to missing part of the system.

Was this another of those experiments designed by that well known Physicist, JC (John Clees) from the Ministry of Silly Questions? It rather reminds me of a GCE practical from long ago when we had to measure surface tension by floating a needle and then dragging it up the meniscus with a magnet. Comments? I can't easily think of a worse projectile. Pingpong balls are designed for maximum interaction with the air. You need something small and dense to minimise air interaction. With the proviso that air resistance can be ignored (not at all true here) your kinematics equations are correct. However there are several questions relating to your energy analysis. Well there was not diagram so I can't tell was acting double or single. Any catapault/bow arrangement applies the tension double, but at an angle. So is the constant calculated for a double band or single? Further is your x distance in the strain energy term in your equation correct or should it be 0.17 cos of some angle? That is: Do the forces in the elastic act at an angle to the displacement? Again a diagram would help. Finally concerning imatfaal,s point 4. Energy is a scalar so does not act orthogonally to anything. Your energy balance is lacking a term as is your kinematic analysis. This does not matter in the kinematic analysis since the term is zero at launch, but does affect the energy balance. The intial vertical velocity is zero. Upon striking the ground the ball has acquired a vertical velocity, whose kinetic energy exactly equals the loss of potential energy due to the vertical drop.

With respect should that not be infinitesimally close, infinitely distant?

Ha Ha, but There was a serious message in my comment. Are you familiar with the story of the famous Ancient Greek Philosophers and the Horse's teeth?

Bear in mind this thread is about art v (sorry Mike) in science, and so we are comparing the art with the (applied) science in the bridges.

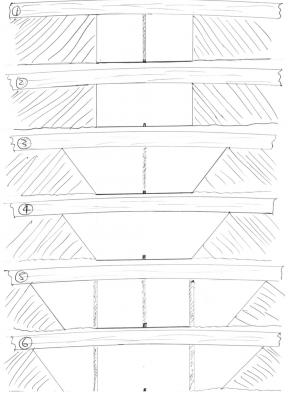
Is this art or science Here are 6 possible arrangements of a motorway overline bridge crossing twin carriageways. Which do you prefer to approach? Which do you find most aestetically pleasing? My apologies for the squashed nature of the sketches. It is interesting to note that Arrangements 1 to 6 are arranged in increasing order of cost. They are also arranged in decreasing order of accident rate.