-
Posts
18482 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
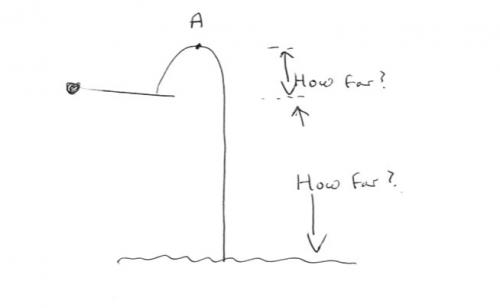
Well your diagram should look something like an upside down hockey stick over the diving board. Look carefully at this diagram and my list of questions in post 4. You should be able to answer the first four just by looking at the diagram. You only need one formula to obtain your answer (my question 5) from this information, not lots of them. Let us work through the firstr four and then think about 5.
-
Are you asking this as someone who understands proper statistics and its proper uses? Statistics makes for a better, safer world by providing quality control tools. There not even a sniff of a definition.
-
Have you drawn yourself a diagram? Do you know the formula for the final velocity, given the initial velocity, acceleration and distance covered?
-
Whilst it will continue to run once already running, an electric motor will not start without auxiliarly help. The purpose of the capacitor is to provide a phase shifted supply (That is the alternating supply is connected to bothe main winding and the capacitor) to a second winding that is used to start the motor. Motors often have centrifugal switches to disconnect the capacitor once the machine is running.
-
Sure, you must know some equations of motion under constant acceleration. To start you off I will redescibe what happens with annotated questions. The person jumps (which way) off a diving board. When he reaches his max 0.6m above the board 1) What is his velocity at this point? 2) What is his total height above the water? 3) What distance does he travel to hit the water? 4) What his acceleration? 5) what is his final velocity? Can you do the problem now?
-
Why is the thread title element 531, when you are referring to an alleged element 534 in your post?
-
You can connect any componeent to AC or DC but The interaction with any component is, in general, different for AC and DC. For instance a capacitor can pass AC, but not DC. However it can store DC, but not AC. As to switches and their ratings. You will often find the same switch with a lower rating for DC than for AC. This is again because of the different response (yes even humble switches have different responses). When a switch closes some arcing inevitable occurs. This damages the contacts by pitting. Perhaps you remember the old fashioned pre electronic ignition system of points in a car? If this passage of current is always in the same direction (DC) then this can lead to corrosion and enlargement of these pits and eventual failure of the switch. Continuous reversal as in AC does helps even out the situation. As a matter of interest Ask yourself 'What is the meaning of AC' and then ask yourself 'What, therefore, is AC current?'
-
Don't you also require carbon as well as heat to reduce iron oxides to iron? Iron will burn if you heat it hard enough, so I don't think heat alone will do it.
-
I don't think the story will be on the net, but here is something other than traffic news about it. Unfortunately it demonstrates all too well that you should not believe all you find on the net. This links say 'built in the 1990s' But my CV tells me that I was the senior engineer constructing the project from 1979 - 1981. http://www.sabre-roads.org.uk/wiki/index.php?title=Obridge_Viaduct
-
I'm sorry? You need to remove energy not add it.
-
Yes, I've seen that happen. The pig troughs (sorry parapet visual enhancement panels) on the Obridge Viaduct.
-
I have my doubts that it would ever be possible to perfectly preserve fracture surfaces and then exactly align them. However I seem to remember cold fusion bonding being achieved in ultraclean labs between two samples of suitable material. Not broken material, but specially prepared material. So that is probably the nearest we will ever get. Sorry I don't have a proper reference, but I will try to find one. And like I said there is the problem of the energy released. You do not want this to go into the newly formed lattice since this is exactly the right energy to break a bond. So it must be removed somehow.
-
About as free as you are to draw a moustache on the Mona Lisa. I have seen some pretty ugly (query unartsome) items designed by engineers, along with some pretty impractical stuff designed by the artistic professions. That is why the Royal fine Arts Commission is one party involved in the design of major bridges in the UK. Often, however good engineering leads to attractive design for example the work of Maillart. This is one of thequestions - like maths plus physics understanding - where disparate disciplines are inseparable in the best. That is the real difference between Man and Machine - The ability to combine apparantly unrelated matters into a whole that is unachievable by other means.
-
Then I suggest you summarise your ideas (or at least the main one) in 5 lines or so in a direct post. That will attract the best attention.
-
Well that's exactly it. Artistic techniques (which produce Art) can be used, very effectively for communication of ideas. An example of where you would not have swansont's cut and dried Newton's law would be found in my paper concerning cracks in concrete. The presentation version of the paper contains several animations of crack patterns and their development in concrete. These greatly aid communication to the subject matter. Cracks vary, every crack pattern is different, but characteristics of similarity can be extracted, from which much useful information can deduced. In case you are wondering; Cracks in concrete duh! So What? Well unwanted cracking has cost hundreds of millions or more worldwide so the subject is big, big business, as well as interesting science.
-
Looking quickly at the material in post#1 I can't see any reason for awarding a -1 vote, so I am going to add a +1. The material itself does seem to refer to highly suspect mystic nonsense. I had to look up 'sonic-geometry' on google to get an inkling of what you are discussing. I watched the beginning of a half hour video of challengeable claims about geometry and stopped at the point where they claim 'The basis of all angle measure is 60.' Which is, of course, just not true. I suggest you look for material that has been much better studied, developed and more rigorously tested such as group and symmetry theory. This is utterly fundamental to our current best way of viewing and understanding Nature. And the best part is that, compared to most branches of mathematics, it is really simple. That is it's great stength and beauty. You do not have to try to get your head round something like relativity to understand it.
-
I deliberately used the word particles, not molecules. This brings up several interesting related points. Gravity does indeed cause aggregation of particles. Some cosmology theory relating to heavenly body formation and growth relates to this. However gravity is not as strong as molecular bonds. If this were not so then any object you picked up would fall apart under gravity. Conversely gravity is not strong enough to put them back together either. John Cuthber has pointed out that breaking many 'solids' (particularly crystalline ones) involves breaking molecular bonds. Many materials are mixtures and indeed the lesser-than-molecular forces that hold these together will allow separation under gravity. So I said particles because particles includes molecules and larger (though still minute) material aggregates. Which comes back to surface energy and fracture reconstruction. Yes you would need to extract energy to perform reconstruction. You would also need a mechanism to perform this. Remember also that, as swansont has already pointed out, oxides form rapidly on fracture surfaces. This is because if you do break a molecular bond in fracturing, then you have an unattached bond end seeking a home to balance the valency of the molecule and the ever present oxygen in the air happily supplies this.
-
That's good since the same situation applies to all matter in all states. The particles at the surface are not in equilibrium. The interior particles are. And yes an ocean has less energy than all the water spread out into droplets and the larger the free surface of anything the more energy it has, to maintain this disequilibrium. This is why droplets try to pull themselsves into balls - to minimise the surface area to volume ratio. Breaking and reforming are the converses of this manifestation of surface energy.
-
Do you understand how surface tension arises in liquids? If not I will draw a helpful diagram.
-
Even though the pieces appear, to the naked eye, the same after the break as before, they are not. When you break something into parts you create new surfaces. This takes energy input. Every part with a new surface has more energy than before, by the amount of this additional surface energy. The theory of fracture mechanics is based on this fact and evaluating this energy and its effects.
-
You need to realise that the calorific value is the total amount of heat obtainable by complete burning of the fuel until no burnable material is left. Thus there can be no product B that has any further calorific value. For instance the complete combustion of carbon results in carbon dioxide, which is incombustible. No further heat can be obtained from the dioxide. Partial combustion results in carbon monoxide, which can be burned further to carbon diode with the release of more heat. The total heat avilable is the same whether you do the combustion completely in one stage to dioxide or in two, first to monoxide and then to dioxide. This heat is the calorific value of carbon. Enthalpy is a different concept entirely, although it is often measured in a calorimeter, and takes into account other forms of energy change such as mechanical work. So what would you like to do now?
-

Will there be no more major discoveries in chemistry?
studiot replied to Elite Engineer's topic in Chemistry
Well yes, for some reason that is all they seem to mention in schools. But really there has been tremendous development in chemistry during the second part of the twentieth century. I am reading a really good book at the moment Introduction to Surface Chemistry and Catalysis by Gabor A Somorjai (Wiley ISBN 0-471-03192-5) You should find this much easier to find than the last British book I recommended. Fantastic developement of surface chemistry since I studied at university in the 1960s. Structural Chemistry and Materials Science in general have both also proceeded at a pace in the second half of the twencen. Analytical chemistry has changed beyong all recognition from the early twencen to the latter part. Chromatography, spectroscopy, Xray microscopy, .... In the first part of the twencen organic chemistry looked like Mrs Beatons cookery book. Pies, Cakes, Puddings, Roasts etc Alkanes, Alkenes, Alkyn, olefines and other homologous series. This has all been replaced by functional groups and reactions - nucleophilic, electrophilic, substitution etc. This has all lead to Plastics, carbon fibres, nanotubes, fancy drugs, kevlar, modern agrichemicals, a revolution in paint chemistry, a revolution in cement chemistry, chemical waste processing, the discovery of long chain compounds using other atoms than carbon ....... the list goes on What's your brew? -
Did you see this bit from the Boeing link About carbonfibre plus aluminium?
-
I can only suggest you re read your own thread title, where you asked "How to evaluate.....?" I am trying to tell you how to do just that in accordance with currently accepted definitions; neither you nor I have the power to change these at whim. Your equation is not an equation at since since the left hand side does not, by your own words, equal the right hand side. I live 150 miles from imatfaal. What do you think he would say if I said to him? "just pop over on your bike, it's only 10 miles - the other 140 can be discounted because they are boring and of no consequence."
-
Beware your bike is not lost in the Southern Ocean. (Poor taste I know, but I couldn't resist it) http://www.boeing.com/commercial/aeromagazine/aero_07/corrosn.html http://www.bikeforums.net/road-cycling/222592-carbon-aluminum-don-t-mix.html http://www.boatdesign.net/forums/materials/corrosion-between-al-carbon-2609.html http://www.rcgroups.com/forums/showthread.php?t=1652668 Road salt?