studiot

I can't comment on the numbers in your subsequent example as there is not enough information. But the above quote is a sound basis to start. Both A and as Sensei pointed out atmospheric oxygen, have chemical bonds which are broken and release energy. The combustion results in B, and some of this released energy goes into forming the new bonds in B. Some of this energy may go into a change of state of, if for instance the fuel is coal or oil and the result is carbon dioxide and water. What is left over appears as heat and is converted to electricity, ignoring the inefficiency of the generation process (this is far from negligable). Further, what Sensei was probably trying to say is that 1kg of A plus some kg of oxygen makes more than 1kg of B. That is you need to take the mass of oxygen into account in your reckoning. The relative masses of hydrogen, carbon and oxygen are 1, 12 and 16 So for every 1kg of hydrogen completely burned 8kg of oxygen are required. For every 1k of carbon, 16*2/12 = 2.7 kg of oxygen are required. So you see the oxygen soon mounts up to a significant portion of the mass of B.

I am not sure what you think is modulating what to create beats. Nothing actually travels instantaneously, I believe I said it was sensibly so. Consider the distance from A to B is about 0.3m An elastic signal travelling in the steel travels at 6000 m/s An elastic signal travelling in the air travels at 340 m/s The bell in struck with a hammer (at A), not continuously excited. So at the moment of imapct at A the part of the sidewall at A deflects. This causes a local pressuse disturbance around A. At this instant B is undeflected as is the local air around it. From the diagram you can see that the disturbance in the steel has to travel about the same distance as the disturbance in the air (=0.3m) So in the time for the disturbance in the steel to reach B and cause an elastic deflection there the distrubance in the air around A travels 0.3 x (340/6000) = 0.017m so it has not reached B, by a large margin This is why I am suggesting that the elastic disturbances at A and B in the air can be considered contemporaneous. This is an additional step to the usual analysis you will find for a piston in air because the piston is being driven at all points simultaneously. What the above shows is that the impact at one point on my bell has the same effect as if the whole bell was excited at once. The usual analyis a la a piston can then be applied and it become a question of geometry. That is the size of the radiator relative to the size of the wave. When the radiator size is comparable to (or much bigger than) the wave size, an off axis listener can receive waves from different parts of the radiator at different times because she is at different distances from different parts of the radiator. These waves can interfere and cause directionality as I previously noted. This effect is most marked at right angles to the main axis. But remember that the size of my bell is smaller than the wavelength of the signal I am observing. I can draw some helpful diagrams if you are interested.

Oh dear, rktpro, yes the equation is wrong. That blooming velocity, c keeps turning up in the wrong place. Unfortunately I don't speak LaTex so I write all my equations out in MathType and then paste them into the text. This time I wrote it in Word and pasted them in there and finally pasted it again into SF. Mea culpa. The correct equation is [math]Y = B\sin \omega \left( {\frac{x}{c}} \right)\cos \omega t[/math] The original two equations should have x/c as well. This does not alter the points made, however since the point is that the original waves contain additions (or subtractions) within the angle, of a time and distance function, reduced to common units. The composite of the two waves into a single standing wave results in the separation of time and distance into the product of a time function and a distance function.

Good morning function. All sound sources much smaller than the wavelength can be considered as an equivalent sphere. There is indeed much theory using equivalent spheres as it is important to the theory of both binaural hearing and stereophonic sound reproduction. As frequency rises the wavelength gets shorter and the sound emitted gets more directional. The higher frequencies contain all the directional information. A spherical wave contains no directional information. This is why it does not matter where you place a bass loudpeaker in a room and indeed you only really need one bass speaker. It is also why animals, such as bats and dolphins, use high frequency for location. For interest here is a short table of frequency and wavelength 50 Hz 6.90 metres 500 Hz 0.69 metres 1000 Hz 0.34 metres 5000 Hz 0.07 metres 15000 Hz 0.02 metres You can see that at 500Hz it need a pretty sizeable source to be bigger than the wave.

You might like to look at Ehrenfest's Paradox. http://en.wikipedia.org/wiki/Ehrenfest_paradox

What exactly am I supposed to make of this? What is it a reply to, did you not read my post? Do you think 6000 is a few thousand? I would say a few thousand is more than 1000 but not more than 3000. This is the figure you will find published as I noted. I further note your Wikipedia link is self admittedly half finished and does not publish any figures.

Setting aside all the personal remarks I will take one statement and ask you for detailed backup. The figures I have quoted were published by the Applied Research Laboratory of Pennsylvania State University in Acoustics Today. If you disagree with these then I look forward to your detailed alternative figures along with your substantiation of them. I am still looking forward to your detailed mathematical analysis requested in my post#16.

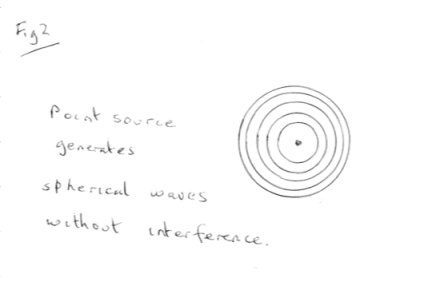
You have alluded several times to my educational background. It seems that not only did we have different professors of mechanics at university; we also had different professors of etiquette. I have not once disputed that the bell has flexural modes of vibration, or that the one we are both concentrating on is flexural. In fact I described such vibrations very early on in posts# 4, 8 and 10 and posted links to many pictures of the same. I did not explicitly state the mode of vibration, just described it as complex, which it is, although this information was available in the links. It was a good addition to the thread for you to state this explicitly as flexural or bending in your post# 15. Flexural vibrations are not sound waves. Sound waves are pressure waves that travel at the speed of sound in the medium. Flexural waves have a different speed and equation. However we are discussing sound in the air, not in the bell. OK let us examine the mechanics of the situation. I stated in post# 10 that the bell launches a spherical wave into the surrounding air. This is in agreement with my measurements around my test bell. That is the readings possess spherical symmetry. There are no measurable nodes or antinodes and the wave is not, as you stated in post# 21 composed of standing waves. There is no measurable interference. This implies that the bell should be considered as a single point source, emitting a single expanding spherical wave. To see how this can arise and why the relative speeds of sound are important look at diagram (1) Points A and B are on opposite sides of a bell, which is immersed in undisturbed air. The constant that has the dimensions of velocity in the differential equation describing flexural vibrations of plates and bells has a value of a few thousand m/s at the frequencies observed. The speed of sound has a value approaching six thousand m/s, as already noted. The theory of elasticity requires that any elastic disturbance, imparted at A, is transmitted as rapidly as possible through the metal of the bell to B. It further requires that the maximum speed is the speed of sound. So any disturbance imparted at A will create a disturbance locally in the adjacent air. The disturbance through the metal of the bell will reach B some 10 to 20 times faster than the disturbance around the outside of the bell since the airborne disturbance travels at 340m/s, since both paths are essentially the same length. When the disturbance in the metal of the bell reaches B, the elastic response at B generates a disturbance in its own right in the air local to B. The point about this is that the response at B is effectively instantaneous so B can be considered to be launching its part of the wave at the same moment as A. Another way of putting this is to say that the wave at B is in phase with the wave at A or that time zero is the same for both points or that the wave centres from A and B are coincident. This is important because it is our justification for the statement that the bell is a single point source generating an expanding spherical wave centred somewhere in the middle of the bell. It is also in complete accordance with conventional wisdom that sound sources smaller than the wavelength of the sound generate spherical waves based on a single point source. So we have an expanding sound field generated by the bell acting as a single point vibrating source, that looks like diagram (2). There is no interference since a single wave cannot directly interfere with itself. Which brings us nicely to the issue of interference. The principle of superposition states that the resultant motion is the sum of the individual motions acting separately. So for any two waves Ytotal = y1 + y2 Now a spherical acoustic wave has both real and imaginary parts in its equation of motion. But I am going to take a plane wave since it has only real parts for simplicity in the next analysis. [math]{y_1} = {A_1}{\omega _1}\left( {x - ct} \right)[/math] [math]{y_2} = {A_1}{\omega _2}\left( {x - ct} \right)[/math] In general since omega1 is not equal to omega 2 the sum of these two travelling waves yields a modulated travelling wave. In general the sum may not have periodic zeros. However by suitable choice of constants and making omega1 equal to omega2 we find after a bit of trigonometric reduction on the sum [math]Y = {y_1} + {y_2} = B\sin \omega x\cos \omega ct[/math] This is the equation of a standing wave since the first (sine) term has periodic zeros distanced in space between points in space specified by omega times x, regardless of the time t. The point is that the wave (a cosine) is multiplied by a sine wave, which has periodic zeros. Thus this equation is the equation of a standing wave and is how nodes arise. Now you have stated categorically that standing waves interfere. So please show mathematically how the superposition (sum) of two such waves can interfere to form zeros or nodes. You have also mentioned that the harmonics of the vibration die away more quickly than the fundamental. Yet you claim energy analysis is irrelevant at best and misleading at worst. The energy in the harmonics of an oscillator increases with harmonic number. The higher the harmonic more energetic it is. Thus as energy is lost to the vibrating system through dispersion and/or dissipation, the energy to power the highest harmonic is lost first. And so on down the list. This is commonly observed in vibrating systems. OK so we have generated an interference free expanding spherical wave in the room, but we are here to explain the why the sound level is lower inside the bell. What is different? The only thing that is different is that the air inside the bell is significantly more confined that outside. Here are a few calculations to show how this makes a difference. The room volume is V0 = 3x2x10 = 60 cubic metres The bell volume is [math]{V_2} = \pi \left( {{{0.2}^2}} \right)\left( {0.15} \right) = .02[/math]cubic metres And the bell surface area is 0.2 square metres Say the average movement is 0.01 mm = 2x10-5 metres Then the volume change on compression is –2x10-6 cubic metres (note negative for compression) Now the volume and pressure changes follow the adiabatic gamma law with gamma = 1.4 So For the room [math]{P_0}V_0^{1.4} = {P_1}V_1^{1.4}[/math] and for the inside of the bell [math]{P_0}V_2^{1.4} = {P_3}V_3^{1.4}[/math] Since the original pressure P0 is the same in both equations solve each for P0 and equate. [math]\frac{{{P_1}}}{{{P_3}}} = \frac{{V_3^{1.4}V_0^{1.4}}}{{V_1^{1.4}V_2^{1.4}}}[/math] Now if we observe that V0 = 60 cubic metres and V1 = (60 - .000002) cubic metres we can approximate V0/V1 = 1 Thus [math]\frac{{{P_1}}}{{{P_3}}} = {\left( {\frac{{20000}}{{20002}}} \right)^{1.4}} = 1.00014[/math] Which very clearly states that the pressure generated outside the bell (P1) is greater than the pressure inside (P3) and of the correct order since sound pressure levels are measured in parts per million relative to normal absolute (1bar). But we should further note that these are absolute pressures in order to use the adiabtic gas laws. The sound pressure level (spl) is actually a pressure difference between the quiescent pressure and the wave pressure. That is spl outside = (P1 - P0) and inside = (P3- P0) We could calculate these by using a standard value for P0 eg (1bar) and I will leave that as an exercise. So is detailed discussion of the modes of vibration of the bell or standing wave interference really necessary to answer the question?

73% of 50 is exactly 36.5. Where you count the maybes as yes or no where does the half a response come from? Hence the comments in the other posts.

Was the moisturising lotion London Pride or Fullers Winter? Both these also come in half pints for those who get half cut and make half _ssed statements.

I think that the difficulty arises at least in part becuse you are thinking that manipulation in John's post#2 and in your book implies multiplication. It does not. It implies composition of functions. The output of composition is another function. I am going to assume you understand what a function is, please ask if you are unsure as this is an important concept. In your notation y is a function of x. We can obtain a second function properly called "the derived function" by following certain rules, known as differentiation. The derived function is often abbreviated to the derivative. However you should realise it is a function in its own right. Moreover it is a function of x (not y). So we can attempt to obtain a derived function from it. I say attempt because not all derived functions are suitable to provide a derived function. If successful, the second derived function will also be a function of x. A pity you are not being taught by my old A level maths teacher. He was the best teacher I have ever had in any subject. He used to insist that when we performed differentiation we made clear the variable concerned by writing "differentiate with respect to x" or d.w.r.x for short. You always got a mark for that even if you fluffed the algebra of the differentiation itself. This practice is good in more advanced work since it helps keep track of things. To recap, differentiation operates on functions and its output is a function. Consequenctly we can repeat this operation multiple times, following the rules for composition of functions each time.

Enthalpy, we seem to have difficulty communicating to an extent that you have attributed several statements to me that I did not make and then proceeded to argue against them. So let us try discussing one statement at a time. In your post#15 you seem to be suggesting that the fact that the speed of sound in steel is some 15 to 20 times that in air is irrelevant. In truth this fact is absolutely vital to the nature and distribution of the sound waves generated by the bell, both in the air inside and outside the bell. It should further be noted that the the bell itself is a single oscillator and not undergoing wave motion.

It's a history of molecules, valency and molecular bonding from earliest times, by a London professor of and practising industrial chemist (mainly pharmacy if I remember correctly). Yes it leads up to the Kekule inspiriation of ring molecules, but discusses all the necessary precursor work, including the blind alleys. There are many more amusing tales, including failure to know or distinguish story of cis and trans isomers that led to mass poisoning. It also includes plates of original documents. I found the copy I read in my local library. In the UK we have something called interlibrary loans. The library should be able to obtain any book in print for a nominal fee. http://www.amazon.co.uk/s/ref=nb_sb_noss?url=search-alias%3Dstripbooks&field-keywords=chasing%20the%20molecule%20buckingham

These questions are set at end of school / beginning of university level. As such you will have had substantial grounding in physical chemistry before they were issued. Have you read the homework help rules? http://www.scienceforums.net/topic/75772-read-this-before-posting-in-homework-help/ Start with part 1 which is the simplest. What rules or laws do you know that might be pertinent?

A really good account is given in the book Chasing the Molecule by Julian Buckingham (Sutton Publishing 2004)

I beg to differ. The sketch by light meow is strictly bias modulation, not amplitude modulation, which produces a different curve. It is what you would achieve if you set a function generator to the higher frequency in lightmeow's sketch and manipulated the output bias control in accord with the lower frequency waveform. True amplitude modulation appears about the zero line as here https://www.google.co.uk/search?tbm=isch&hl=en-GB&source=hp&biw=&bih=&q=amplitude+modulation&gbv=2&oq=amplitude+modulation&gs_l=img.1.0.0l10.812.4469.0.6969.20.14.0.6.6.1.344.2079.0j8j2j1.11.0....0...1ac.1.34.img..4.16.1921.8jkP2z__saQ Mathematically if the main wave is A * sinw1t Where A is a constant called the amplitude we get amplitude modulation if we multiply A by a second sin frequency thus B * sinw2 t* A * sinw1t What lightmeow has drawn is what happens if we add a second frequency sin wave to the original waveform. A * sinw1t + B * sinw2t

Why can't it's state, position and speed be determined? I define it to be 1kg mass and travelling at 100mph along the y axis. I then ask to calculate the force required to accelerate it to 200mph in 10 seconds. If you really don't like my example, then try this one where the object is not the only thing inthe universe. Place a point mass, mass m, ( a perfectly respectable object in theoretical mechanics) Place it at the exact centre of a uniform spherical shell of total mass M and diameter 1000 metres. What force is required to displace this mass from the centre and accelerate it in any direction at 1m/s2?

I've made no assumptions. I've simply applied the theory based on the mathematical principle that if an equation holds for all x then it must hold for any particular value I choose.

I doubt that anyone would award me a knighthood, but thanks. The short answer is yes but I will have to give it some thought, before a fuller reply. Obviously the modulus controls the strength of the restoring force that generates the oscillation and thus affects the amplitude. But there is also a big difference in density between water and air and it is the density variation that distorts voices in other gasses such as helium by affecting the speed of sound.

Swansont's answer give a clue as to why a wave travelling in one direction can meet another wave travelling in a different direction, the two waves have a conflab at their meeting point, and then pass through each other each going their separate ways as if they had never encountered each other. This is entirely different behaviour from that of solid particles. Energy does not preserve direction, momentum does.

I'm sorry, I no longer have the sensors capable of submersion. I last studied and used underwater acoustic profiling and positioning systems in the late 1970s/ early 1980s. Here is the meter I was using for this thread. It is a very versatile multimeter that I keep in the toolbox.

So what have I said that was controversial? ***************************************************************************************************************************************************** Function, I don't know if you are still following this thread but here is a simple experimental analogy to what is happening. Take an ordinary bicycle pump. Remove the handle, complete with shaft and piston. Crank the shaft and piston backwards and forwards in the same motion that it would follow inside the pump sleeve. Do you feel significant air resistance? Now put the inner assembly back inside the pump sleeve and repeat the action. What do you notice? You should notice that there is a significant fixed resistance due to sidewall friction. But there is also increasing resistance the more you compress the air inside. This is because the air inside the pump is confined, whereas the free air in the atmosphere is not. Just as I said in post#4 about the difference between the air inside and outside the bell. This analogy is not exact but follows the same principles. The pump is rather more dramatic because the air in the bell is loosly confined whereas the air in the pump is tightly confined. You can perform further experiment, this time on waves and resonance, with your pump. Try to pump backwards and forwards at different rates and observe what happens.

If there was only one mass, m1 then Newton's second law Finertial = m1a Still holds. Why do you wish to deny it? However Newton's law of gravity woul still hold, but Fgravitational = km1m2/r2 so Fgravitational = 0 since m2 = 0 There is nothing inconsistent here to be a matter of opinion about.. If the equations said something different then I would report that.

No Consider a universe where there is a single particle with mass. There is still inertia, measured by Newton's second law, but there is no gravity.

Perhaps someone typed this expression into the nav computer of the missing plane?