-
Posts
18258 -
Joined
-
Last visited
-
Days Won
104
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
Since the (flat?) end of the rod is much smaller than the rigid plane I would start by modelling the wave as a plane wave. The wave will be the same whether the rod is moving and strikes the plane or the something like a large hammer with a flat face strikes a stationary rod. Solutions to the latter are well developed in the literature. Such devices are used in oceanography and seismology. Avoid hammers striking drums that is a different situation. If the rod is long you will need to consider Rayleigh waves developing at the surfaces.
-
Look up the name Hannes Alfven - he got a Nobel prize for this stuff.
-
Integration is often most useful as summation, adding in the contributions of very small parts of a whole. That is what you are describing in this case. It is better not to think of dV as a variation but as a small part of the whole.
-
The problem (why is this not in homework?) should say whether the rod is brought to rest at the point of impact or if it bounces off.
-
The OP said nothing about the mass being fixed or otherwise. Why would the mass be fixed? That implies that either the radius or the density decreases as the length increases. that makes no sense. The fact remains that it takes an engine twice the effort to run up a shaft of twice the length, but the same material and diameter. I think the important point to make to the OP is that there is one property that varies with the volume, but without regard to shape and we call that the mass. For any shape whatsoever the mass = volume times the density. But the moment of inertia contains information about the distribution of that mass and depends not only on the volume but the shape of that volume and therefore the distribution of the mass in it. I think it is legitimate to assume constant density for that exercise. I did also say in post#3 that we really need more detail.
-
But if you increase L, do you not increase m?
-
Since the OP asked about a solid cylinder, the answer is yes it does. However, ScienceStudent, you need to be a good deal clearer about what you mean. We would not normally develop the moment of inertia in terms of volume. The axial moment of inertia is Wr2/2g so it depends upon length inasmuch as we add up the contributions from all the disks along the length, but tell us more about what you book says for further comment.
-
There was an interesting article in the New Scientist, dated 18 Jan 2014 about the decade between AD 534 and AD545 where a large part of the human populations were decimated in civilizations right round the world, asociated with a sudden large drop in global temperature that lasted a decade. The geological reasons for the tmeperature drop are uncertain at best. Does anyone have any more information to contribute?
-
http://www.allaboutcircuits.com/vol_3/chpt_2/8.html If this was too far advanced for you back up to the beginning of the chapter.and watch the video lectures. http://www.allaboutcircuits.com/vol_3/chpt_2/1.html
-
Luke, I'm not saying you are right, I'm not saying you are wrong. I'm testing your text for self consistency. If you ever (try to) publish it will be tested much more thoroughly by a whole battery of experts. Now you state In my two posts (two lines and three lines) in this thread, Where exactly did I repeat that the strong force is fundamental? Please do not base your arguments on words I did not utter. Having dispatched that, let us return to what I did say. I said (and repeated) that I consider your argument circular or self referential because it replaces one force with another. "A rose by any other name is still a rose" You need to address this point. I don't care if it is fundamental or not, that is not the point. The problem for modern physics is that any form of 'Force' represents 'action at a distance', which is frowned upon. To recap. So far my one and only point is that you have renamed what others call the strong force by introducing alternative forces. All my other words are an attempt to explain this. I did indeed understand your replacement mechanism but you have replaced the strong force with an effect what is still a force. Over to you.
-
No the development of the argument is definitely circular (self referential if you like) when you use something to define itself. The strong nuclear is one of the four (three?) fundamental forces in standard theories where the force action is replaced by some other mechanism than a 'force' (eg mediating particles). All you have done is said that one force is really the result of the action of a different force, without explaining further.
-
What wqould be good would be if you were to devote a post to expanding upon each of your bullet points, in particular this one This description seems like a circular argument to me since you are using forces (repulsion/attaraction) to describe forces (strong nuclear force).
-
No I meant an arrow launcher, as a one dimensional diaphragm. But there are many examples of devices using a two dimensional diaphragm to exert an output force in a way that conforms to the definition I gave earlier by springing against a support reaction.
-
With the greatest respect, it's still more interesting to many than some of the stuff that has been posted lately. I suggest a good start would be to agree what a machine is. One common definition is a device for applying an output force at one point by means of an input force applied at some other point. The forces may be the same of different in both direction and magnitude. I do not know what the good professor had in mind, perhaps something based on a flexible diaphragm, such as used by American Red Indians in the past.
-
Mathematical Physics B D Gupta is over 1000 pages of good solid information to have on your bookshelf, and readily available in India. go well
-
That does not answer this statement extracted from my link. As I understand it this would require charge to change sign under transformation from a left handed coordinate system to a right handed one, something we know does not happen.
-
q as a psuedo scalar? How would that work? http://en.wikipedia.org/wiki/Pseudoscalar
-

understanding about directional derivative
studiot replied to bingliantech's topic in Analysis and Calculus
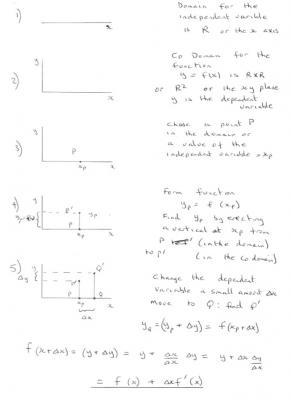
OK so here is the first part of what I think Strang means. I will try to keep to short sentences. It is very important to understand what variable are and what a function is. So I have started with the simplest. A variable can be dependent or independent. The simplest function has one of each type. A function also has a domain and a co-domain. They are not always the same. The domain is the set that includes all the values of the independent variable(s), the co-domain includes all the values of the dependent variable. I am going to use R, the set of all Real numbers as the domain (independent variable). In other words the x axis. This is fig(1) in my sketch. In order to draw a graph and construct a function y = f(x) I need to have a co-domain that can hold number pairs (x, y). This is called R2 or RxR and ie represented by the xy plane. y is the dependent variable. This is fig(2) in my sketch. To construct our function we choose a point P in the domain with value, xp This is fig(3) in my sketch. We calculate the value of y at x=xp as yp =f(xp) and plot P' in the co-domain. This is fig(4) in my sketch. If we now move to another value Q of the independent variable, x, with a small change [math]\Delta x[/math], we can calculate the change in the dependent variable resulting from the change in the independent variable. Now in this simple case there is only one direction of change for the independent variable (ignoring sign). That is along the x axis. So the f'(x) that we calculate by the formulae in my fig (5) is the directional derivative for this case. It depends only on [math]\Delta x[/math] This is what Strang meant by we might expect to divided by [math]\Delta x[/math] When we look at the case of two independent variables in the next instalment, things are more complicated. The domain is now R2 not R and the co-domain now R3 not R2. (can you see a pattern here?) But we must go through the same steps 1 - 5. Please confirm that you have understood this so that we can proceed. -
Good point. Further KE is not a function of relative velocity.
-
That's not possible. There must be forces acting on A an B in or against the direction of motion, other than friction.
-
Lord and Wilson : the Mathematical description of Shpe and Form Gasson : The Geometry of Spatial Forms Faux and Pratt : Computational Geometry for Design and Manufacture
-

understanding about directional derivative
studiot replied to bingliantech's topic in Analysis and Calculus
Yes I've had that one a long time and sometimes recommend it. -

What maths do I need to know to do Calculus
studiot replied to Lightmeow's topic in Science Education
Well, Calculus was originally developed to (suprise suprise) calculate things of interest. These days mathematicians tend to get hung up on the underlying principles, which I think are introduced a little early. Much of everyday and applied calculus consists of standard results we look up rather than work out, especially not from first principles. However you need a good working knowledge of whatever you are applying it to. The goes for both the physics/chemistry/economics and the maths such as geometry or trigonometry. I also recommend you brush up your algebra, considering your thread from just before Christmas. You really do need to be able to understand the answer. Then you can go a very long way with some suprisingly simple calculus. -

understanding about directional derivative
studiot replied to bingliantech's topic in Analysis and Calculus
I have not looked a Strang's Calculus before but have heard a few adverse comments. I did find it it patchy with some quite deep material interspersed with some very superficial treatment, despite the 671 pages. His coverage is much wider than attempted by most authors but many of the little intermediate steps and explanations are missing, so I feel would be any course using this book. Unfortunately this applies to section 13 which you are referring to. In particular he has mixed the vector based approach with the traditional geometric one, omitting important parts of both. We can discuss this further if you wish. Are you familiar with the vector dot product? -

understanding about directional derivative
studiot replied to bingliantech's topic in Analysis and Calculus
What is your text called? I am rather at a loss to understand why anyone would want to divide [math]\Delta f\;by\;\Delta x[/math] as stated in paragraph 2. The text is clearly referring to the 3D situation where z = f(x,y). that is values of the function f(x,y) are plotted as a surface as values on the z axis. It starts off in paragraph 1 by saying just that and that the result is a surface. In fact it hints at the truth which is that even the partial derivatives [math]\frac{{\partial f}}{{\partial x}}\;and\;\frac{{\partial f}}{{\partial y}}[/math] are directional derivatives, the first in the x direction and the second in the y direction. Clearly any other direction has components from both x and y. The point P(x0,y0) is in the plane z=0, as are the steps [math]\Delta x[/math], [math]\Delta y[/math] and[math]\Delta s[/math] In fact you can take a short [math]\Delta s[/math] step in any direction, but you are still in the plane z=0 or the domain of x-y. The chain rule tells us that [math]\frac{{df}}{{ds}} = \frac{{\partial f}}{{\partial x}}\;\frac{{dx}}{{ds}} + \frac{{\partial f}}{{\partial y}}\;\frac{{dy}}{{ds}}[/math]