studiot

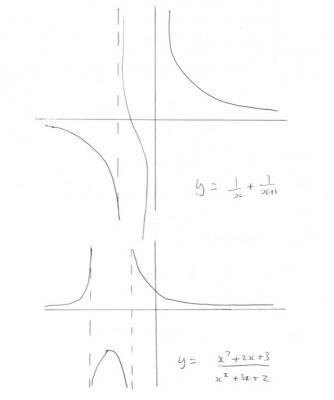
I'm sorry your Stewart is very different from mine, but someone else may have it. Anyway I meant to say you should try sketching this curve. Have you done any curve sketching? Since you have the ratio of two quadratics consider [math]y = \frac{{a{x^2} + bx + c}}{{d{x^2} + gx + h}}[/math] You are asked what happens when x=0, so substitute x=0; what does that mean for h? Here are a couple of fractions involving quadratics (they are not correct but to illustrate points. How many times does the curve cross the x axis? What horizontal and vertical asymptotes are there? What happens when x is large and+ve; large and negative? You need to consider what about the constants place the corssings and asymptotes to match your requirements.

Physica's solution. I have cleaned up the background a bit.

Yes I am aware of that and that this is your specialist field. What you are basically saying is the limit of resolution (nothing to do with Heisenberg) is the interval between two zero crossings. We have to assume that time itself flows evenly within this interval. And yes I am using 'tick' in the most general sense. This is somewhat akin to the limit of spatial resolution of various types of microscope.

Will this not also have a vertical asymptote at x = -1? Your curve is stated to have a single vertical asymptote I don't have your version of Stewart, but in my 1987 version he sketches various cases of vert asym. Does he do that in your book and can you find a type with a single v asympt? A chapter/page ref might be useful for others.

I thought that discussion on relativity had been declared off topic by hypervalentiodine, since we are supposed to be discussing time and the OP. The OP had the sense to realise that no one can tell you what time is. He was seeking 'a basic understanding'. Now one thing to understand is about the flow of time. Here is some quotes from the recent Cambridge University book 'On Space and Time', edited by Professor Shahn Majid. Lizzie L I suspect you would find much of interest in this book. Although the book deals also with the possible granularity of space and time, the following is not in the book The issue of time flowing is interesting because of the way we measure it. Does time flow evenly or jerkily? All clocks proceed unevenly, within a tick cycle. Old fashioned chronometers proceeded with a series of small jerks forwards. More modern atomic clocks still run at uneven rates through their tick cycle, this can be modelled by SHM.

Well the 'curvature effect' would be uneven and somewhat reflect the shape of the object. You would, in principle, be able to deduce the shape of the object from the variation in the curvature 'field'. Note the words in inverted commas are meant to be taken in a somewhat colloquial sense rather than a strict physics one. However most objects on a scale sufficiently large to really exert appreciable gravity are roughly round. Even Saturn and its rings could be called round. There are two effects that promote this. Firstly, surface tension tends to create globular shapes as with raindrops. Secondly, extended shapes are subject to quite large disruptive forces due to twisting and rotation. So they tend to break up.

This is a truly personal question since each of us is different so I can't say if my experience would work for you. However here is my truly personal experience. I did more or less what you are suggesting many years ago for my A levels. I rewrote my class notes , along with other material from books, in the way that I understood it and how I understood it all hung together. This involved quite a few drafts and rewrites - be prepared for that. This helped me greatly to consolidate what I knew and cetainly produced favourable results in the A and S levels. One teacher at the time said famously The more times you write it down the more danger there is you will remember it. A parting point, if this is for you own consumption it does not have to be neat copyplate, just readable. That saves quite a bit of effort. go well

Thank you for the solution paper. My only comment is that i is the unit vector so in deriving H you should have brackets round the kx-kl0 thus H = (kx-kl0)i Otherwise you seem to have solved it. Well done. Would you like me to post your solution until you?

If you are going to introduce equations then you should be prepared to answer legitimate questions about them. I am sorry you appear to feel vindictive about this. Surely it is easier to simply state what you think is travelling at a velocity you have granted it. And no, I do not think you invented relativity, nor was I discussing it. The discovery of the Lorenz transformation preceeded Einstinian relativity and was a practical observation that is actually independent of it.

Well it was clearly you who introduced them. In two out of eight equations you have used the symbol v, which you tell me stands for velocity. Why is it so unreasonable to ask what is travelling at this velocity and in what coordinate system?

So getting back to the Lorentz tranformation, You have stated (correctly) that v is velocity, but have not stated what is travelling at this velocity or what frame it is being measured in. Without this information the formulae given cannot be used.

Correct in this case but, Actually you can transform some derived physical quantities into others with suitable processes, eg the Fourier transform, but see here

Since you introduced the equation (by copying someone else) I'm waiting for you to do some actual mathematics. I have asked you at least five times to explain v, which you also introduced. So far you have told me it is superfluous, and ignored every request to explain in full what this variable represents. So, once again, I am asking you to explain yourself. Why for instance introduce v if it is superfluous?

No it just looks like nonsense to me since the terms have not been defined. since you won't do it I will. If your equation is valid it must hold for every value of v : v<c. So I define v=0. Then your equation tells me that x = x Whoopee!!! Not a rotation or other animal in sight.

Perhaps that's because you are not setting out your 'math' correctly or conventionally. Bald statement of equations, without specifying variables and constants constraints and limits of applicability and developing a train of mathematical argument (proof) does not make 'math'. So you are not going to answer my question?

Yes a velocity indeed, but what velocity in what coordinate system? That is the key question. I really don't care or see that it is relevant that some people have invented yet another superfluous new word called rapidity.

After you explain what the v is in your equations. I have asked several times now. Not at all. xyzt. You can changes any of these. C. Changes in xyz are measured in metres; changes in t are measured in seconds. No magic here. However there may be no change at all. It is fundamental that the coordinates represent independent variables.

Time is measured in seconds, distance in metres. Both by international convention I have no problem with either and no wish to develop alternative units based on c or 'plank' dimensions etc. There is another current thread here where a GCSE student was led to make the classic units mix up because too many non standard units were used in his question. Consistency of units is a big thing of mine. Perhaps swansont will tell us about an old particle physics unit - the barn.

Yes indeed. So explain to me the units on the two types of axes, or explain to me why there aren't two types of axes, or why we don't need units for them. Yes we still have x,y,z,t but remember that there is no absolute coordinate system. That one refers to that entity and that light cone. All measurements in xyzt are as observed by the entity at the apex of the cone. Any other entity will have her own cone with coordinate system x'y'z't' Roger Penrose didn't realise the confusion his beautiful diagram would cause. I still await the explanation of v

With respect, I thought you had picked up the point that we don't. Two independent sets of axes are required. Because as I said we require at least two entities for the comparison The 'transformation' in schneibster's post#158 refers to the mathematical link between them. I await his explanation of v

Michael123456, thank you posting a light cone pic. (post#139) But you have the basic deductive sequence back to front. We note (observe) that we cannot observe the future and posit the light cone explanation. Not the other way round. That is the scientific method. Schneibster, yes it is in the maths. So do you understand what you have posted? If so what is v?

Yes indeed, which is why I objected to the use of the word 'faster' in some earlier posts. There are quite a few instance of physical quantities that have been introduced to satisfy an observed need, Entropy is another. Unlike entropy for which the need is only apparent in sophisticated systems, the need for time is pretty immediately obvious in very simple ones. As you say we even have an innate 'sense' of time. However our perceptions also lead us astray when dealing with subtleties. Your description of drawing curves is a description of the parametric equations of a curve and in many maths books you will find the parameter called t, justified by the addended phrase "since t is often time".

You should be using the MKS system. Length is measured in metres, so bring all lengths to metres (and powers of 10) Force is measured in Newtons Mass is measured in kilograms density is measured in kg per cubic metre. So if your radius is in cm, and therefore your volume is cubic centimetres, your mass will be wrong, and thus your forces will be wrong. You can work in other units, but it is just so easy to make a mistake and get things 10, 100, 1000 times too big or small. That is why I said be consistent. Have we cured the negative sign now?

One of the most important lessons to learn in GCSE is to be consistent in your units. This is why it is recommended to always state them in full. Let us look at your figures. So do you have a 2.5 metre ball? you say the density of the ball is 0.35 whereas the density of the liquid is 1 and a bit. So why does the ball fall at all?

No you are definitely not stupid. If you use the more reply options (button towards bottom right) you will find a way of uploading files to your post. Click the cursor where you want it, after uploading, and it will be displayed there. g is regarded as constant for schoolwork, even at A level. It actually gets smaller and smaller the further from the centre of the Earth you get, so that has to be taken into account for rockets etc. It is normally taken as 9.81 Newtons per kilogram of mass. So a mass of 1kg weighs 9.81 Newtons force. (10 is often a good figure in rough calcs)