-
Posts
18475 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-
I would dispute that your notation is the same as previously posted. The square root function does indeed follow your definition by convention. However the equation (which is not a function) must allow any value that satisfies the equality, by definition. It is important to distinguish between functions and expressions containing an equals sign. When we have an expression containing an equals sign that may be satisfied by more than one value we would normally have additional conditions to satisfy which will determine which one we want. There were several mistakes mades in a recent thread on quadratics by posters failing to observe this simple requirement. So John's statement is a refers to a set of values for x (the domain) and another set of values that picks out a unique member for each value of x. That properly makes it a function. Amaton referred to a specific value of x (16) and presented it via an equals sign. That does not qualify as a function.
-

static friction of masses connected by a rod
studiot replied to inkliing's topic in Classical Physics
Well there are many interesting things that can be deduced about this problem. Tonight was the business carol concert but I did get a chance to scribble a few things down. Now the two weights (allow me the luxury of using W it's much less writing than mg especially in mathml) undergo four different regimes as the inclination increases from horizontal. Two are boundary regimes and fully soluble. 1) When the plane is horizontal there are no horizontal forces acting so there is no external load to provide any force in the rod. the coupled pair of weights act at a single rigid body. 2) When neither are in limiting friction. Whilst there are many solutions, some interesting relationships can be deduced as I have sketched below. Furthermore there are upper and lower bounds on the rod force P. The lower bound can be found from the expression for the force to just prevent sliding down the plane. The upper bound can be found from the expression for the force needed to just start hayuling the smallest weight up the incline. 3) Once the smaller weight is in limiting friction we can gain an additional equation. 4) The second boundary regime occurs when both weights are in limiting friction and supply yet another equation to complete the set. Regime (2) is statically indeterminate but often in a case like this compatibility supplies additional equations. I have to admit I can't think of one her but suggestions are welcome. The theorem of three forces may also be employed. Yes there are four forces acting on each weight (Weight W, Normal reaction N, riction F and rod force P) but F and P are in line so can be reduced to an auxiliary force (F-P). -

static friction of masses connected by a rod
studiot replied to inkliing's topic in Classical Physics
I haven't worked this one out fully, but I see no reason in principle why it should not be possible to calculate the required quantities. You need to be careful with two points however. Firstly only one of the masses will be in limiting friction. This is the key to the solution. Secondly the direction of friction is opposite for the static situation asked for and the for kinetic situation you also describe. -
I don't need you to tell me what potential energy is, thank you. But this is much better discussion. With proper discussion we can maybe rephrase your ideas in proper scientific English. I do need you to explain your case without referring to a whole raft of unrelated websites. First question are you looking as a molecular to subatomic level as implied in one part of your posts? If so what would you make this conductor out of that is as small as an electron? Or are you looking at the scale of materials greater than this, in which case a conductive filament makes more sense. Further the only thing you get when two (or more) magnetic fields intersect is a more complicated magnetic field. Magnetic fields are vector fields and as such add vectorially under superposition. Normal mag fields are also conservative. Does this mean anything to you or do you need further explanation? Well I don't see any personal attack in the above, only offers of help at several places in the text. But I don't like being threatened so I will report this discussiion myself and then leave this thread. go well with your inquiry.
-
I don't need you to tell me what potential energy is, thank you. But this is much better discussion. With proper discussion we can maybe rephrase your ideas in proper scientific English. I do need you to explain your case without referring to a whole raft of unrelated websites. First question are you looking as a molecular to subatomic level as implied in one part of your posts? If so what would you make this conductor out of that is as small as an electron? Or are you looking at the scale of materials greater than this, in which case a conductive filament makes more sense. Further the only thing you get when two (or more) magnetic fields intersect is a more complicated magnetic field. Magnetic fields are vector fields and as such add vectorially under superposition. Normal mag fields are also conservative. Does this mean anything to you or do you need further explanation?
-
Perhaps if you stopped introducing pseudo physics terms and just plain impossible ones and actually stated your case this thread could progress. You haven't answered my question about kinetic potential yet. And now you introduce a 'compressed magnetic field'. If English is not your first language then we can try to help you achieve the correct terms and descriptions, but arrogance and disrespect for those trying to help will not get you very far. No one else here has yet seems to understand what you case is all about so it's over to you. Incidentally even thin film materials move - they flex or exhibit other strain energy properties.
-
Research? Oersted's research should fit your bill https://www.google.co.uk/#q=oersted%27s+experiment Just because you posted nonsense doesn't invalid my other comments, they still stand.
-
You have posted this is 'Modern and Theoretical Physics' Why? Have you given any thought to your questions? How can a stationary magnet (your words) produce kinetic potential? What is kinetic potential? What is 'an electrical reaction' ? And why should this be produced? Since it is so easy to test, why don't you test it, why assume anything?
-
Entropy is much misunderstood. Consequently a great deal of rubbish is spouted in its name. A particularly common error, not only in this area but many others, its to ignore the conditions of applicability and then complain that it is 'wrong'. You have expressed a common doubt, however so well done for thinking about it. Entropy increase or stasis applies to a finite system as a whole. Further, since entropy change deals with change, it does not tell you anything about how a system is, only where it is going. Saying that 'the (necessarily infinite) entropy, mass, energy or anything else of a an infinite system increases' makes no sense. You can easily have local variations within a system where entropy rises or falls or remains the same. So your first question needs to be Is the universe finite or infinite?
-
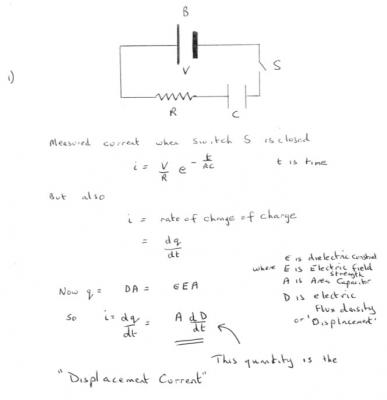
Well you are asking about displacement current, although they are from your diagram which you posted without labelling the axes or any of the variables or any explanation of the diagram. There is no magnetic field involved in displacement current. S1 and S1 are surfaces, but you are still ignoring my comments Why is this? I asked if you have studied vector calculus, because your diagram is from an advanced treatment of displacement current using vector calculus that would be undertaken by someone who already knows what it is. I mentioned Gauss theorem ( which is one of Green's several theorems) which allows a vector surface integral to be converted to a line integral around a closed path and allows us to consider displacement current in free space in total generality. I also said I would post a simpler treatment for you. The first thing to know is that several physical quantities are known by more than one name or have had their names changed over the years. The first important quantity to know this about was originally called the dielectric constant and is now usually known as the 'permittivity' and given the symbol epsilon [math]\varepsilon [/math]. Epsilon is of course a constant, not a variable, and is a property of the space concerned or the substance filling that space. It is only of general interest for nonconductors since an electric field can exist in the space containing a nonconductor. We use another constant for space containing a conductor called the conductivity, sigma [math]\sigma [/math]. So we can have an electric field inside a non conductor or dielectric. We measure the strenght of the field by the Electric Field Strength, given the symbol E. I have shown this in bold because E is a vector. That is it has a magnitude and direction at any point - a bit like the strength of the wind at any point. Now we come to the good bit. Years ago a second physical quantity was defined equal to the field strength times the dielectric constant and called the Displacement. [math]D = \varepsilon E[/math] Not suprisingly it was given the letter D It is also a vector since it is a number times a vector. Nowadays the Displacement is called the Electric Flux. Again originally, experiments showed that if we set up apparatus as in my figure (1) which shows a battery connected to a conductor R in series with a capacitor C and supply a voltage through a switch S then a measurable current flows. This current changes with time as in the equation noted. That is starts off large and gets smaller and smaller, eventually dying away to nothing. To complete the circuit this current must not only flow through the conductor R, but also through the capacitor C. This is very important and was not originally understood. How could a current flow through a non conductor? Well Maxwell suggested that since there is an electric field and therefore a Displacement that this strange effect be called Displacement Current and the name has been kept, even though the name of the quantity D has been changed. We now know that the conducted current is the result of a steady electric field and the displacement current is the result of achanging electric field. If you wish to know more there is a second figure to explain this. But please let me know how you got on with the part 1 first.
-
I currently dealing with a server emergency this morning, but will be back to hopefully post this evening that should be a bit easier to digest. Meanwhile please don't let me stop others offering explanation.
-
I have noticed that some posters are more sensitive than others, and further that some posters find difficulty in communicating. The trouble is that whilst in face to face communication we can often determine this and compensate, in a forum we cannot immediately see the effect of our words. Sometimes there is an overresponse to a flippant or (apparently) inconsiderate remark. Now I see nothing wrong with saying something along the lines of, Sorry I didn't mean to offend and rephrasing or just continuing with the substance of the thread, just being more careful subsequently. But this does not seem to be done very often.
-
No. This will go much better if you respond to my comments. A path is a route or track in space, just like the footpath along the side of a road, or my route on the surface of the earth. Suppose I went from London to Chicago. That is an open path on the surface of the earth. Now suppose i went London to Chicago to Wellington to Hongkong to Abu Dhabi and back to to London. That is a closed path on the surface of the earth. In your case your path is a circle in a plane so is closed.
-
Well P is a circle, but the important thing is it is a closed loop, it could be a square or any shape so long as it is a single closed loop. As a closed loop P is the boundary of surface, S1. All the current I must pass through this loop or surface. I is the total current and is the sum (integral) of all contributions of curent density J across the whole of S1. If the density is uniform then it is just J x Area. We can use Gauss Theorem to relate the flux through the gap across the area to the size of the loop ie path P, if you have studied the necessary vector calculus. Next question? (note this is understanding displacement current the hard way.) Now a question for you. I don't understand why you have posted this in Quantum theory. It is classical physics, due to Maxwell.
-
Well it's a very pretty picture, but what is the question?
-

Inhomogeneous diffusion equation on the half plane
studiot replied to LeehLee's topic in Homework Help
In fairness Leehlee has attempted to solve his (her?) problem. I suggest you look at Chapter 6 ( The Diffusion Equation) of Sneddon : Elements of Partial Differential Equations. Your equation is a one dimensional version of the heat equation, which is treated by several methods including Green's Functions. -

Finding a Absolute Value Quadratic - Math Team
studiot replied to Lightmeow's topic in Linear Algebra and Group Theory
Doing algebra with moduli is more tricky than ordinary algebra so I'm suprised to find it on the High School syllabus - it didn't used to be. Anyway I thought you hung in there rather well. Keep it up for the future and you will do well. -

Finding a Absolute Value Quadratic - Math Team
studiot replied to Lightmeow's topic in Linear Algebra and Group Theory
Well I'm pleased to receive a response, even if it was not a correct one. If |x|=x2+x-3 Then rearranging x2+x-|x|-3 = 0 x2+(x-|x|)-3 = 0 x2+(x-x)-3 = 0 : x>0 x2+(x-(-x))-3 = 0 : x<0 02+(0-0)-3 = 0 : x=0 which implies x cannot be zero Thus there are, as I said, two equations to solve. One does indeed lead to x = +/- sqroot(3), but subject to the the condition x>0 so we must discard the negative root and only accept the positive. You can check this by substitution into the original expression. I think Halls made transposition error in his second equation, somehow changing the sign of the 3. (post#4) thus the second equation factorises as (x+3) (x-1) = 0 with the condition that x<0 This time we must discard the positve root and accept the negative x=-3 again we can check this by substitution. So this quadratic does indeed lead to two solutions as expected. But then you made a mistake in your first presentation (post#1) since you stated that |x| = x2+x-3=0. Which implies that |x| = 0. Which implies that x = 0. Again I ask, does b ever = 1? go well -
Does the first part of of your parabola statement make sense? " P1 is the set of all P (xy) contained in P1 " I have used P1 for your script P.
-

What is the different between momentum and inertia?
studiot replied to Lightmeow's topic in Classical Physics
Let us say you have a train comprising a locomotive of mass ml pulling a carraige of mass mc at velocity, v via a long chain. What is the momentum of the train? The locomotive runs into the buffers. What is the momentum of impact? -

Temperature and pressure change in a diffuser
studiot replied to Laura Morrison's topic in Engineering
What you require is known as the steady flow energy equation. This considers both the total mass and the energy within the system to be constant However what you have is homework and needs to be in the homework section. You did state your thoughts at starting and the SFEE is a formalised equation combining Bernoulli and thermodynamics, so U1 + P1V1 + KE1 +PE1 + Q = U2+ P2V2 + KE2 +PE2+ W This can be developed to set some of these quantities to zero, given your conditions, and using specific (per mass) quantities, to solve your problem. You will also need the mass continuity equation. There's lots about it on the net, but come back to discuss your problem further if you wish. https://www.google.co.uk/#q=steady-flow+energy+equation the Manchester article is very good and probably similar to the approach in your college. -
It should be pointed out that the magnitude of the Coriolis force or effect depends upon size of the moving system or range of movement. That is why it is (sometimes) significant in the path of winds and ocean current.
-

Finding a Absolute Value Quadratic - Math Team
studiot replied to Lightmeow's topic in Linear Algebra and Group Theory
Shouldn't this be in the homework section? Here is a hint. Go back to the beginning and ask yourself What makes you think b=1? A modulus often means you have two equations to solve. -
I have no idea what this means.
-
Not directly, but you could regard the pairing of two electrons in an orbital, thereby lowering their combined system energy, as a form of attraction.